Karnaugh haritası

Karnaugh haritası (KM ya da K-map) (İngilizce) Boolean cebri'ndeki ifadeleri sadeleştirmek için kullanılan bir yöntemdir. Maurice Karnaugh 1953'te Edward Veitch'in 1952'te keşfettiği Veitch tablosunun geliştirilmiş ve elektrik devrelerine odaklanmış versiyonu olarak tanıtıldı. Veitch tablosu ve Karnaugh haritası bu yüzden Marquand-Veitch diyagramı ve Karnaugh Veitch haritası (KV maps) olarak da bilinir.Karnaugh haritası insanların örüntü tanıyabilme kabiliyetini kullanarak karışık hesaplamaları sadeleştirir. Aynı zamanda potansiyel hata durumlarının hızlıca fark edilmesini ve ortadan kaldırılmasını kolaylaştırır.
Gerekli Boolean sonuçları iki boyutlu doğruluk tablosundan Karnaugh haritasına aktarılır. Karnaugh haritası, dışındaki hücrelerin Gray kodu ile sıralandığı ve bu hücrelerin yatay-düşey birleşimlerinin temsil ettiği her hücrenin bir giriş durumunun temsil edildiği bir haritadır. Haritadan 1 ve 0'ların standart formlardan birini oluşturan ideal grupları belirlenir. Bu gruplar ihtiyaç duyulan Boolean ifadesinin asgari terimle yazılmasında kullanılabilir. Karnaugh haritaları fiziksel devrelerde minimum sayıda mantık kapısı kullanılması için gerçek dünyadaki mantık gereksinimlerini sadeleştirmede kullanılır. Çarpımların toplamı ifadesi her zaman VE kapılarının bir VEYA kapısını beslemesiyle gerçekleştirilir. Toplamların çarpımı ifadesi ise VEYA kapılarının bir VE kapısını beslemesiyle gerçekleştirilir. Karnaugh haritaları aynı zamanda yazılım tasarımlarındaki mantık ifadelerini sadeleştirmek için de kullanılır. Boolean ifadeleri, koşullu durumlarda olduğu gibi okuması ve sürdürülebilmesi zor ve karmaşık hâle gelebilir. Ancak bir kez sadeleştirilen kod standart formlara getirildikten sonra VE- VEYA kapıları kullanılarak direkt gerçekleştirilebilir. Basit mantık ifadelerini sadeleştirmek için şematik ve mantıksal yöntemler Orta Çağ'dan beri bulunmakta. Karmaşık ifadeleri sadeleştirmek için daha sistematik metotların geliştirilmesi ise 1950'lere dayanıyor ancak 1980'lerin sonuna kadar pratikte en çok kullanılan yöntem Karnaugh haritasıydı.
Örnek
Karnaugh haritaları Boolean cebrinde yazılmış fonksiyonları sadeleştirmek için kullanılır. Örneğin, aşağıda doğruluk tablosu verilmiş Boolean fonksiyonunu inceleyin.
| A | B | C | D | f(A,B,C,D) | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | 0 |
Aşağıda, Boolean değişkenleri A,B,C,D ve onların tümleyenleri kullanılarak yazılmış, Boolean cebrindeki aynı fonksiyonun iki farklı sadeleştirilmemiş gösterimi bulunmaktadır.
- , haritadaki miniterimler (doğruluk tablosunda çıktısı 1 olan satırlar).
- , haritadaki maxiterimler (doğruluk tablosunda çıktısı 0 olan satırlar).
Karnaugh haritası

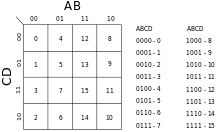
Yukarıdaki örnekte 4 farklı değişken 16 farklı şekilde gruplandırılabilir, bu yüzden doğruluk tablosunun 16 satırı ve Karnaugh haritasının 16 durumu var. Karnaugh haritası 4 x 4 oluşturuldu.
Satır ve sütün indisleri (Karnaugh haritasının üstünde ve solunda gösterilen) ikilik sayı sıralamasına göre değil de Gray kodu ile sıralandı. Gray kodu sayesinde ardışık hücreler arasında sadece 1 bit değişeceğinden emin olunuyor. Tamamlanan bir Karnaugh haritasının her bir hücresi, o kombinasyondaki girdiler için fonksiyonun oluşturacağı çıktıyı temsil ediyor.

Karnaugh haritası oluşturulduktan sonra doğruluk tablosundaki bilgiler, fonksiyonun sahip olduğu en basit formlardan birisini (standart form) oluşturmak için kullanılır. Karnaugh haritasındaki ardışık 1'ler ifadeleri sadeleştirebilmek için gruplanabilir. Miniterimler bu 1'lerin gruplanmasıyla elde edilir. Miniterim grupları dikdörtgen olmalı ve alanları ikinin katı olmalıdır (1, 2, 4, 8...). Miniterim dikdörtgenleri herhangi bir 0 değerini içermeden mümkün olan en geniş dikdörtgen olmalıdır. Gruplar içerisindeki hücreler farklı dikdörtgenler tarafından birden fazla kullanılabilir. İdeal gruplar aşağıda yeşil, kırmızı ve mavi çizgilerle işaretlenmiştir, kırmızı ve yeşil gruplar çakışır. Kırmızı grup 2 x 2 bir kare, yeşil grup ise 4 x 1 bir dikdörtgendir, kesişen kısımlar kahverengi ile belirtilmiştir.
Hücreler genellikle daha kolay gösterim için o hücreyi kapsayan girdilerle ifade edilir. Örneğin, AD, A ve D'nin doğru olduğu 2 x2'lik alanı(yukarıda 9,11,13,15 nolu hücreler) kapsar. Diğer taraftan AD ise A'nın doğru ve D'nin yanlış olduğunu (D doğru) gösterir.
Karnaugh haritası toroidaldır, yani dikdörtgen grupları köşelerden birleşebilir. (görsele bakınız). En sağdaki hücreler, en soldakilerle ve en üstteki hücreler, en alttakilerle komşuluktadır. Bakıldığı zaman karşılık gelen girdiler sadece bir bit farklıdır (gray kodunda ardışıktır).Bu yüzden AD gruplanabilir ve üstteki 12,8 alttaki 10,14 hücrelerini içine alır. Aynı mantıkla BD, dört köşeyi gruplayarak elde edilir.
Çözüm

Karnaugh haritası oluşturulduğunda ve komşuluktaki 1'ler gerekli şekilde gruplandığında cebirsel miniterimler, hangi 1'lerin aynı kutularda kaldığına bakılarak bulunabilir.
Kırmızıyı gruplamak için:
- A, kutu boyunca sabit ve 1 değerinde. Bu yüzden kırmızının temsil ettiği miniterimin cebirsel ifadesinde bulunmalı.
- B, kutu boyunca sabit bir değere sahip değil, bu yüzden dışlanmalı.
- C, değişmemekte. Kutu boyunca 0 olduğu için tümleyeni (NOT-C) alınmalı. Bu yüzden ifadede C olmalı.
- D, kutu boyunca sabit bir değere sahip değil, bu yüzden dışlanmalı.
Bu yüzden Boolem çarpımların toplamı gösteriminin terimlerinden biri AC olmalı.
Yeşili gruplarken, C ve D değişirken A ve B sabit kalıyor. B'nin değeri 0 ve dahil edilmeden önce tümleyeni alınmalı. Bu yüzden bir diğer terim ise AB. Fark edildiği üzere yeşil ile kırmızı gruplandırma kesişti ve bunda herhangi bir sakınca yok.
Aynı şekilde mavi kutu bize BCD terimini veriyor.
Bütün grupların terimlerini birleştiriyoruz. Devrenin normal formu:
Göründüğü üzere Karnaugh haritası aşağıdaki sadeleştirmeyi yapmamızı sağladı.
Bu ifadeyi boolean cebrinin aksiyomları ile de sadeleştirebilirdik ancak sadeleştirmenin alacağı zaman terim sayısı ile üslü olarak artacaktır.
Tersini Alma
Fonksiyonun tersi, aynı metod ile 0'ları gruplayarak çözülebilir.
Tersini kapsayacak bütün terimler gri kutularla ve farklı renkte sınırlarla gösterilmiştir.
- kahverengi: A, B
- altın rengi: A, C
- mavi: BCD
Buradan fonksiyonun tersi :
olmuştur.
De Morgan'ın yasalarını kullanarak, toplamların çarpımı bulunabilir.
Umursanmayan Durumlar

Karnaugh haritası aynı zamanda doğruluk tablosunda umursanmayan değerler olan fonksiyonlar için daha kolay sadeleştirmeler yapmamıza olanak sağlar. Umursanmayan durumlar tasarımcının çıktısını umursamadığı girdilerdir. Bu yüzden dikdörtgen gruplara eklenebilirler de eklenmeyebilirler de,hangi şekilde daha büyük kutular oluşturulabiliyorsa o tercih edilmelidir. Haritada genellikle X ya da - ile ifade edilirler.
Sağdaki örneğin üsttekinden farkı f(1,1,1,1) olan değerin umursanmayan durum olarak değiştirilmesidir. Bu durum kırmızı dikdörtgenin, haritanın altına kadar genişlemesine olanak sağlar ve bu sayede yeşil olarak gösterdiğimiz kutucuğu ortadan kaldırarak ifadeyi sadeleştirir.
Yeni basit denklem :
Görüldüğü üzere ilk terim sadece A, AC değil. Bu durumda umursanmayan durum sayesinde bir terimden kurtulduk (yeşil), birini sadeleştirdik (kırmızı) ve birinden hata tehlikesini(bir sonraki hata tehlikesi bölümünde gösterildiği gibi sarı terimden kurtulduk) kaldırdık.
Fonksiyonun tersi aşağıdaki gibi sadeleşir.
Hata tehlikesi
Eleme
Karnaugh haritaları hata tehlikelerini bulmakta ve kaldırmakta kullanışlıdırlar. Hata tehlikelerini Karnaugh haritalarında tespit etmek çok kolaydır çünkü bunlar sadece komşu ancak aynı kutunun üyesi olmayan bölgelerde gerçekleşebilir. Bununla birlikte, Gray kodunun doğası gereği ardışık bu bağlamda yukarıda anlatıldığı gibi özel bir anlama sahiptir, aslında bir dikdörtgen değil torus boyunca hareket ediyoruz.
- Yukarıdaki örnekte, olası bir hata tehlikesi C 1, D 0 iken ve A 1, B ise 1'den 0 a (mavi bölgeden yeşil bölgeye giderken) değişirken vardır.Bu örnekte, çıktı sabit 1 kalmak üzere tanımlanmış ancak bu geçiş denklemde özel bir terimle kapsanmadığından olası bir hata (çıktının anlık olarak 1'e geçişi) mevcuttur.
- Aynı örnekte bulunması daha zor ikinci bir olası hata vardır: D 0, A 1, B 1, C 1'den 0'a geçerken (mavi bölgeden kırmızı bölgeye). Bu durumda hata, haritanın üstünden altına wraps.

Hatanın gerçekten olup olmayacağı ve olması konusunda endişelenip endişelenmesi gerektiği uygulamanın fiziksel doğasına bağlıdır.Saatli mantıkta, istenen zamanda değişkenin değerinin belirlenmesi yeterlidir ancak örnekte saatli mantık gözetilmemiştir.


































