Küresel koordinat sistemi, üç boyutlu uzayda nokta belirtmenin bir yoludur.

Matematikte sinüs, trigonometrik bir fonksiyon. Sin kısaltmasıyla ifade edilir.

Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.

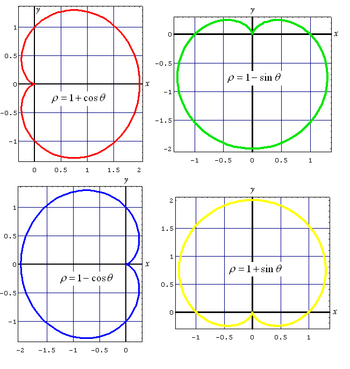
Matematikte gül veya rodonea, kutupsal koordinat sisteminde çizilmiş bir sinüs ya da kosinüs eğrisine denir. Gül eğrisi, aşağıdaki kutupsal denklemle ifade edilir:


Logaritmik spiral, doğada sık rastlanan bir spiral çeşididir. İlk olarak 17. yüzyılda René Descartes ve Jakob Bernoulli tarafından tanımlanmış ve incelenmiştir. Bernoulli bu eğriye, kendine özgü matematiksel özelliklerinden dolayı, spira mirabilis adını vermiş ve mezar taşına bir logaritmik spiral oyulmasını vasiyet etmiştir.

Hiperbolik spiral, kutupsal koordinat sisteminde


Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda potansiyel teorisi olarak da bilinmektedir.
Gauss integrali, Euler–Poisson integrali olarak da bilinir, tüm reel sayılardaki e−x2 Gauss fonksiyonunun integralidir. Alman matematik ve fizikçi Carl Friedrich Gauss'dan sonra adlandırlıdı. İntegrali şöyledir:

Fresnel integrali, S(x) ve C(x), iki transendental fonksiyon'dur. Augustin-Jean Fresnel'e atfedilmiştir ve optikte kullanılmaktadır. Yakın alan Fresnel difraksiyon fenomeninde ortaya çıkar; aşağıdaki integral gösterimi ile tanımlanırlar:


Matematik'te, beta fonksiyonu, Euler integrali'nin ilk türüdür, 

Euler spirali, eğimi eğrinin uzunluğuyla doğrusal olarak degişen bir eğridir. Euler spiralleri yaygın olarak spiros, clothoids veya Cornu spiralleri olarak da adlandırılır. Euler spirallerinin kırınım hesaplamalarında uygulamaları vardır. Genellikle demiryolu ve karayolu mühendisliklerinde teğet eğrisi ve dairesel eğri arasındaki geometriyi bağdaştırmaya ve aktarmaya yarayan geçiş eğrisi olarak kullanılır. Teğet eğrisi ve dairesel eğri arasındaki geçiş eğrisinin eğimindeki lineer değişim prensibi Euler spiralinin geometrisini belirler:
- Eğimi teğetin düzgün kesitinden başlayarak lineer olarak eğri boyunca artar.
- Euler spiralinin dairesel eğriyle karşılaştığı yerde eğimi dairesel eğrinin eğimine eşit olur.
Görüntü yük yöntemi, elektrostatikte kullanılan bir soru çözüm tekniğidir. İsimlendirmenin kökeni problemdeki sınır koşullarını bazı sanal yükler ile değiştirme yönteminden gelir.
Burada, en yaygın olarak kullanılan koordinat dönüşümü bazılarının bir listesi verilmiştir. Kısmi türevler alınırken çarpımın türevi gibi davranıldığı akıldan çıkarılmamalıdır. Bir örnek olarak  fonksiyonunda üç çarpım vardır
fonksiyonunda üç çarpım vardır
Değişken değiştirme, İntegral, çarpanlara ayırma, denklemler, üslü denklemler, trigonometri ve diferansiyel denklemler başta olmak üzere matematiğin her alanında işlemi basitleştirmek için kullanılan matematiksel bir yöntemdir.

Matematikte Gauss fonksiyonu, bir fonksiyon biçimidir ve şöyle ifade edilir:


Matematikte, küresel harmonikler Laplace denkleminin çözüm kümesinin açısal kısmıdır. Küresel koordinatların bir sistemi içinde küre yüzeyinde tanımlanır, Fourier serisi ise çember üzerinde tanımlanır. Laplace'ın küresel harmonikleri  Pierre Simon de Laplace tarafından ilk 1782 yılında tanıtılan bir ortogonal sistemin küresel harmonik formlarının özel bir kümesidir. Küresel harmoniklerden birkaçının kökleri sağda gösterimlenmiştir. Küresel harmonikler pek çok yerde teorik önem taşımaktadır ve özellikle atomik yörünge elektron konfigürasyonları, yerçekimi alanları, geoitleri ve gezegen ve yıldızların manyetik alanlarının temsili ve kozmik mikrodalga arka plan radyasyonu karakterizasyonu hesaplanmasında kullanılan pratik uygulamaları vardır. Küresel harmonikler 3D Bilgisayar grafiklerinde, dolaylı aydınlatma ve 3D şekillerin tanınması gibi konularda geniş bir yelpazede özel bir rol oynamaktadır.
Pierre Simon de Laplace tarafından ilk 1782 yılında tanıtılan bir ortogonal sistemin küresel harmonik formlarının özel bir kümesidir. Küresel harmoniklerden birkaçının kökleri sağda gösterimlenmiştir. Küresel harmonikler pek çok yerde teorik önem taşımaktadır ve özellikle atomik yörünge elektron konfigürasyonları, yerçekimi alanları, geoitleri ve gezegen ve yıldızların manyetik alanlarının temsili ve kozmik mikrodalga arka plan radyasyonu karakterizasyonu hesaplanmasında kullanılan pratik uygulamaları vardır. Küresel harmonikler 3D Bilgisayar grafiklerinde, dolaylı aydınlatma ve 3D şekillerin tanınması gibi konularda geniş bir yelpazede özel bir rol oynamaktadır.

Birim çember Matematikte, yarıçapı bir birim olan çembere birim çember denir. Çoğunlukla, özellikle trigonometride, Öklid düzlemine göre Kartezyen koordinat sisteminde, merkezi orijin üzerinde (0,0) olan ve yarıçapı bir birim olan çemberdir. n birim çember sıklıkla S1; olarak ifade edilir. Genellikle daha büyük boyutları ise birim küredir. (x, y) birim çember üzerinde bir nokta olduğunda, |x| ve |y|, dik olan ve hipotenüsü bir olan üçgenin diğer kenar uzunluklarıdır. Bu nedenle, Pisagor teoremine göre, x ve y bu denklemi karşılamaktadır.

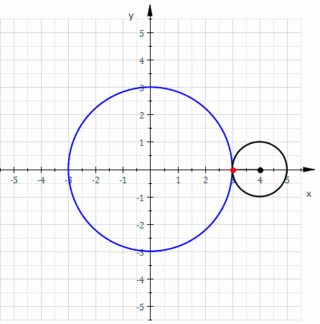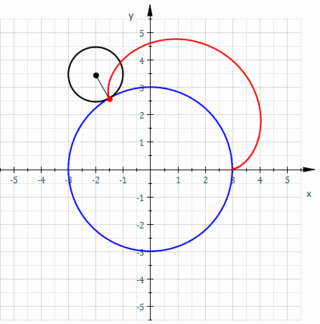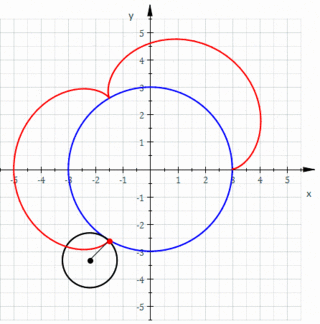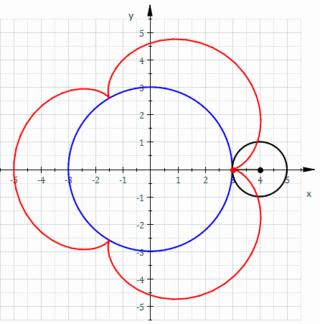
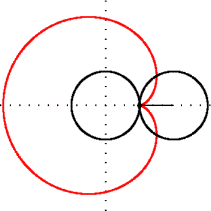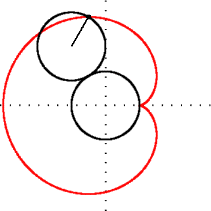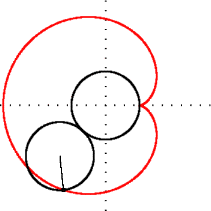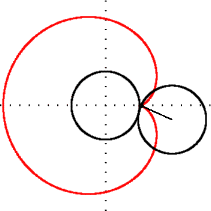
Geometride, bir episikloid, sabit bir çemberin etrafında kaymadan yuvarlanan bir çemberin çevresi üzerinde seçilen bir noktanın yolunu izleyerek üretilen bir düzlem eğrisidir -buna episikl (epicycle) denir. Bu, yuvarlanma eğrisinin özel bir türüdür.

Matematikte, bir parametrik denklem, bir grup niceliği parametreler olarak adlandırılan bir veya daha fazla bağımsız değişkenin fonksiyonları olarak tanımlar. Parametrik denklemler genellikle bir eğri veya yüzey gibi geometrik bir nesneyi oluşturan noktaların koordinatlarını ifade etmek için kullanılır ve sırasıyla parametrik eğri ve parametrik yüzey olarak adlandırılır. Bu gibi durumlarda, denklemler, toplu olarak nesnenin parametrik temsili veya parametrik sistem, veya parametrelendirilmesi olarak adlandırılır.

Geometride hipotrokoid, R yarıçaplı sabit bir çemberin içinde yuvarlanan r yarıçaplı bir çembere bağlı olan bir nokta tarafından izlenen bir yuvarlanma eğrisidir, burada nokta iç çemberin merkezinden d kadar bir mesafededir.