
Yer çekimi, kütleçekimi ve merkezkaç kuvvetinin birleşik etkisi nedeniyle nesnelere aktarılan net ivmedir. Yönü bir şakul topuzuyla çakışan, gücü veya büyüklüğü  normuyla temsil edilen vektörel bir niceliktir.
normuyla temsil edilen vektörel bir niceliktir.

Fizik, fiziksel kimya ve mühendislikte akışkanlar dinamiği, akışkanların akışını tanımlayan akışkanlar mekaniğinin bir alt disiplinidir. Aerodinamik ve hidrodinamik dahil olmak üzere çeşitli alt disiplinleri vardır. Akışkanlar dinamiğinin, uçaklardaki kuvvetlerin ve momentlerin hesaplanması, boru hatları boyunca petrolün Kütle akış hızının belirlenmesi, hava durumu modellerinin tahmin edilmesi, uzaydaki bulutsuların anlaşılması ve fisyon silahı patlamasının modellenmesi dahil olmak üzere geniş bir uygulama yelpazesi vardır.

Elektrostatik, duran veya çok yavaş hareket eden elektrik yüklerini inceleyen bir bilim dalıdır.

Akışkanlar dinamiği alanında, Reynolds sayısı, farklı durumlarda akışkan akışı desenlerini tahmin etmeye yardımcı olan bir boyutsuz sayıdır ve eylemsizlik kuvvetleri ile viskoz kuvvetler arasındaki oranı ölçer. Düşük Reynolds sayılarında, akışlar genellikle laminer akış tarafından domine edilirken, yüksek Reynolds sayılarında akışlar genellikle türbülanslı olur. Türbülans, akışkanın hız ve yönündeki farklılıklardan kaynaklanır ve bazen bu yönler kesişebilir veya akışın genel yönüne ters hareket edebilir. Bu girdap akımları, akışı karıştırmaya başlar ve bu süreçte enerji tüketir, bu da sıvılarda kavitasyon olasılığını artırır.
Fizikte ve matematikte, matematikçi Hermann Minkowski anısına adlandırılan Minkowski uzayı veya Minkowski uzayzamanı, Einstein'ın özel görelilik kuramının en uygun biçimde gösterimlendiği matematiksel yapıdır. Bu yapıda, bilinen üç uzay boyutu tek bir zaman boyutuyla birleştirilerek, uzay zamanını betimlemek için dört boyutlu bir çokkatlı oluşturulmuştur.

Olasılık kuramı ve istatistik bilim dallarında gamma dağılımı iki parametreli bir sürekli olasılık dağılımıdır. Bu parametrelerden biri ölçek parametresi θ; diğeri ise şekil parametresi k olarak anılır. Eğer k tam sayı ise, gamma dağılımı k tane üstel dağılım gösteren rassal değişkenlerin toplamını temsil eder; rassal değişkenlerin her biri nin üstel dağılımı için parametre  olur.
olur.

Akışkan statiği ya da hidrostatik, hareketsiz akışkanlar üzerinde çalışmalar yapan akışkan mekaniğinin dalı. Hangi akışkanların durağan dengede hareketsiz kaldığıyla ilgili yapılan çalışmaları kabul eder ve akışkan dinamiğiyle karşılaştırıldığında hareket halindeki akışkanları inceler.
Knudsen sayısı, moleküler ortalama serbest yol ile kabaca ölçülebilir uzunluk skalasının oranını veren boyutsuz sayıdır. Bu uzunluk skalası, örneğin, bir sıvının içinde yer alan bir cismin çapı olabilir. Knudsen sayısı adını Danimarkalı fizikçi Martin Knudsen'e (1871-1949) atfen almıştır.
Sıkışabilir akışkan bir ortamda yol alan herhangi bir araç ya da gövde ye ait burun konisi kısmının aerodinamik tasarımındaki, önemli bir problem burun konisinin geometrik şeklinin belirlenmesidir. Burun konisinin şekli optimum performans için gereklidir. Dönel katı cisim şekil tanımlamasının gerektiği işler gibi birçok uygulamalar, akışkan bir ortamda çok hızlı hareket eden böyle bir cismin karşılaşacağı direncin en aza indirilmesini gerektirir.

Yöney alan, Öklid uzayının seçilen bir alt kümesinin her bir noktasında yöneyin belirlenmesidir. Düzlemdeki bir yöney alanı, her biri düzlemdeki bir noktaya ilişik, yönü ve büyüklüğü olan oklar topluluğu olarak düşünülebilir.
Akışkanlar dinamiğinde Darcy-Weisbach eşitliği, uzun bir boruda akan bir sıvının sürtünme kaynaklı yük ve basınç kaybıyla alakalı olaybilimsel bir eşitliktir. Eşitlik ismini Henry Darcy ve Julius Weisbach'tan almaktadır. Darcy-Weisbach eşitliği Darcy sürtünme faktörü olarak da bilinen boyutsuz sürtünme faktörünü içerir. Ayrıca Darcy-Weisbach sürtünme faktörü ve Moody sürtünme faktörü olarak da bilinir. Darcy sürtünme faktörü 4 katı olduğu Fanning sürtünme faktörü ile karıştırılmamalıdır.
Fizikte, dairesel hareket bir nesnenin dairesel bir yörünge boyunca bir rotasyon ya da çemberin çevresinde yaptığı harekettir. Rotasyonun sürekli açısal değeriyle birlikte düzgün ya da değişen rotasyon değeriyle düzensiz olabilir. 3 boyutlu bir cismin sabit ekseni etrafındaki rotasyon parçalarının dairesel hareketini içerir. Hareketin denkliği bir cisim kütlesinin merkezini tanımlar.
Einstein-Hilbert etkisi genel görelilikte en küçük eylem ilkesi boyunca Einstein alan denklemleri üretir. Hilbert etkisi genel görelilikte yerçekiminin dinamiğini tarifleyen fonksiyonel işlemdir. metrik işaretiyle, etkinin çekimsel kısmı, 

Parçacık fiziğinde elektrozayıf etkileşim, doğanın bilinen iki veya dört temel etkileşiminin birleşimin bir tanımıdır: elektromanyetizm ve zayıf etkileşim. Her gün düşük enerjilerde, bu iki kuvvet çok farklı oluşsa da, teori modelleri aynı kuvvetin iki farklı etkisi gibidir. Yukarıdaki birleştirme enerjisi, yaklaşık 100 GeV, tek bir elektrozayıf kuvvet oluşturabilir. Bu yüzden, eğer evren yeterince sıcaksa (Big Bang'den kısa bir sonra olan bir sıcaklık ortalama 1015 K), elektromanyetik kuvvet ve zayıf kuvvet birleşmiş bir elektrozayıf kuvvete dönüşür. Elektrozayıf dönem boyunca, zayıf kuvvet güçlü kuvvetten ayrılır. Kuark dönem boyunca, elektrozayıf kuvvet elektromanyetik ve zayıf kuvvetten ayrılır.

Temas açısı  , bir damlanın sıvı-buhar sınırı ve katı yüzey arasında buluşan açıdır. Young denklemi ile katı bir yüzeyin bir sıvı tarafından ıslatılabilirliğini ölçmektedir. Belirli bir sıcaklık ve basınçta belirli bir katı, sıvı ve buhar sistemi benzersiz bir denge temas açısına sahiptir. Bununla birlikte, uygulamada, ilerleyen (maksimal) temas açısından çekik (minimal) temas açısına kadar değişen dinamik bir temas açısı histerezisi fenomeni sıklıkla gözlenmektedir. Termodinamik denge teması bu değerler dahilindedir ve bunlardan hesaplanabilir. Termodinamik denge temas açısı, sıvı, katı ve buhar moleküler etkileşiminin göreceli gücünü yansıtır.
, bir damlanın sıvı-buhar sınırı ve katı yüzey arasında buluşan açıdır. Young denklemi ile katı bir yüzeyin bir sıvı tarafından ıslatılabilirliğini ölçmektedir. Belirli bir sıcaklık ve basınçta belirli bir katı, sıvı ve buhar sistemi benzersiz bir denge temas açısına sahiptir. Bununla birlikte, uygulamada, ilerleyen (maksimal) temas açısından çekik (minimal) temas açısına kadar değişen dinamik bir temas açısı histerezisi fenomeni sıklıkla gözlenmektedir. Termodinamik denge teması bu değerler dahilindedir ve bunlardan hesaplanabilir. Termodinamik denge temas açısı, sıvı, katı ve buhar moleküler etkileşiminin göreceli gücünü yansıtır.
Matematik ve fizikte Elwin Bruno Christoffel'in adına atfedilen Christoffel sembolleri eğri uzaylardaki metrik farkı düzenler.Daha basit bir biçimde anlatmaya çalışırsak bir vektörü gösterdiğimiz kartezyen koordinat sistemi gibi düz koordinatlarda vektörün bileşenlerini temsil eden baz vektörler kendi eksenlerine dik olduğu için türevleri sıfıra eşittir. Fakat eğri bir uzayda baz vektörler de değişir yani türevlenir. İşte bu türev işlemi Yunan alfabesinden  harfi ile temsil edilmektedir. Christoffel sembollerinin fizikte birçok uygulaması vardır. Bunlardan en önemlisi Einstein alan denklemlerinde kullanılmasıdır.
harfi ile temsil edilmektedir. Christoffel sembollerinin fizikte birçok uygulaması vardır. Bunlardan en önemlisi Einstein alan denklemlerinde kullanılmasıdır.
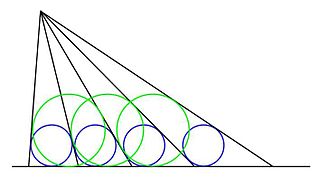
Geometride, eş iç teğet çemberler teoremi bir Japon Sangaku'sundan türetilir ve aşağıdaki yapıya ilişkindir: belirli bir noktadan belirli bir çizgiye bir dizi ışın çizilir, öyle ki bitişik ışınlar ve taban çizgisi tarafından oluşturulan üçgenlerin iç teğet çemberleri eşittir. Çizimde eş mavi çemberler, açıklandığı gibi ışınlar arasındaki mesafeyi tanımlar.
Cauchy sayısı (Ca), süreklilik mekaniği alanında, özellikle sıkıştırılabilir akışların çalışılmasında kullanılan boyutsuz bir niceliktir. Bu sayı, Fransız matematikçi Augustin Louis Cauchy'ye atfen adlandırılmıştır. Sıkıştırılabilirliğin önemli olduğu durumlarda, dinamik benzerlik sağlamak için elastik kuvvetler, atalet kuvvetleriyle birlikte göz önünde bulundurulmalıdır. Bu bağlamda, Cauchy sayısı, bir akış içerisindeki atalet kuvvetleri ile sıkıştırılabilirlik kuvveti arasındaki oran olarak tanımlanmakta ve şu formülle ifade edilmektedir:
 ,
,
Akışkanlar dinamiğinde, Eötvös sayısı (Eo), diğer adıyla Bond sayısı (Bo), sıvı yüzeyinin hareketinde yerçekimi kuvvetlerinin yüzey gerilimi kuvvetlerine oranını ölçen bir boyutsuz sayıdır. Viskoz sürüklenmenin etkisini gösteren, genellikle  olarak ifade edilen Kapiller sayısı ile birlikte,
olarak ifade edilen Kapiller sayısı ile birlikte,  , örneğin toprak gibi, sıvının gözenekli ortam veya granüler ortamlarda hareketini incelemek için kullanılır. Bond sayısı, kabarcıklar veya çevresindeki bir akışkanda hareket eden damlaların şeklini karakterize etmek için Morton sayısı ile birlikte kullanılır. Bu boyutsuz terim, sırasıyla Macar fizikçi Loránd Eötvös (1848–1919) ve İngiliz fizikçi Wilfrid Noel Bond (1897–1937)'un adını taşır. Eötvös sayısı terimi Avrupa'da daha sık kullanılırken, Bond sayısı dünyanın diğer bölgelerinde yaygın olarak kullanılmaktadır.
, örneğin toprak gibi, sıvının gözenekli ortam veya granüler ortamlarda hareketini incelemek için kullanılır. Bond sayısı, kabarcıklar veya çevresindeki bir akışkanda hareket eden damlaların şeklini karakterize etmek için Morton sayısı ile birlikte kullanılır. Bu boyutsuz terim, sırasıyla Macar fizikçi Loránd Eötvös (1848–1919) ve İngiliz fizikçi Wilfrid Noel Bond (1897–1937)'un adını taşır. Eötvös sayısı terimi Avrupa'da daha sık kullanılırken, Bond sayısı dünyanın diğer bölgelerinde yaygın olarak kullanılmaktadır.
Marangoni sayısı (Ma), yaygın olarak tanımlandığı üzere, Marangoni akışları ile difüzyon taşıma hızını karşılaştıran bir boyutsuz sayıdır. Marangoni etkisi, sıvının yüzey gerilimindeki gradyanlardan kaynaklanan akışıdır. Difüzyon ise yüzey gerilimindeki gradyanı oluşturan maddenin yayılmasıdır. Bu nedenle, Marangoni sayısı akış ve difüzyon zaman ölçeklerini karşılaştıran bir tür Peclet sayısıdır.





















