
Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.

Öklid geometrisi, İskenderiyeli Yunan matematikçi Öklid’e atfedilen matematiksel bir sistemdir ve onun Elemanlar adlı geometri üzerine ders kitabında tarif edilmektedir. Öklid'in yöntemi, sezgisel olarak çekici küçük bir aksiyom seti varsaymaktan ve bu aksiyomlara dayanarak birçok başka önermeyi (teoremleri) çıkarmaktan ibarettir. Öklid'in sonuçlarının çoğu daha önceki matematikçiler tarafından ifade edilmiş olsa da, Öklid, bu önermelerin kapsamlı bir tümdengelimli ve mantıksal sisteme nasıl uyabileceğini gösteren ilk kişi oldu. Elemanlar, ilk aksiyomatik sistem ve resmi ispatın ilk örnekleri olarak ortaokulda (lise) hala öğretilen düzlem geometrisi ile başlar. Üç boyutlu katı geometrisi ile devam ediyor. Elemanlar’ın çoğu, geometrik dilde açıklanan, şimdi cebir ve sayı teorisi olarak adlandırılan şeyin sonuçlarını belirtir.

Genel görelilik teorisi, 1915'te Albert Einstein tarafından yayımlanan, kütleçekimin geometrik teorisidir ve modern fizikte kütle çekiminin güncel açıklamasıdır. Genel görelilik, özel göreliliği ve Newton'un evrensel çekim yasasını genelleştirerek, yerçekimin uzay ve zamanın veya dört boyutlu uzayzamanın geometrik bir özelliği olarak birleşik bir tanımını sağlar. Özellikle uzayzaman eğriliğine maruz kalmış maddenin ve radyasyonun, enerjisi ve momentumuyla doğrudan ilişkilidir. Bu ilişki, kısmi bir diferansiyel denklemler sistemi olan Einstein alan denklemleriyle belirlenir.

Jules Henri Poincare Fransız matematikçi, teorik fizikçi, mühendis ve bilim felsefecisiydi. Yaşamı boyunca var olduğu şekliyle disiplinin tüm alanlarında mükemmel olduğundan, genellikle bir bilge ve matematikte "Son Evrenselci " olarak tanımlanır.

Diferansiyel geometri türevin tanımlı olduğu Riemann manifoldlarının özellikleriyle uğraşan matematiğin bir alt disiplinidir. Başka bir deyişle, bu manifoldlar üzerindeki metrik kavramlarla uğraşır. Eğrilik, eğriler için burulma ve yüzeyler için değişik eğrilikler, araştırılan özellikler arasındadır.

George David Birkhoff en çok, şu anda ergodik teorem olarak adlandırılan şeyle tanınan Amerikalı matematikçi. Birkhoff, döneminde Amerikan matematiğinin en önemli liderlerinden biriydi ve yaşadığı süre boyunca birçok kişi tarafından önde gelen Amerikalı bir matematikçi olarak kabul edildi.

Matematikte, tensör, çok boyutlu verinin simgelenebildiği geometrik bir nesnedir. Skaler denilen yönsüz nicel büyüklükler, vektör denilen yönlü büyüklükler ve matris denilen iki boyutlu nesneler birer tensördür. Tensör, tüm bu nesnelerin genelleştirilmiş halidir ve çok boyutlu veri kümeleri için kullanılır. Nesnenin kaç boyutla ifade edildiğine de tensörün derecesi denilir. Bir skalerin derecesi sıfır, bir vektörün bir, bir matrisin ise ikidir. Tensörler üç ve üzeri dereceye sahip olabilir.

Diferansiyel geometrinin matematiksel alanı içinde, Levi-Civita paralelkenarımsı bir eğri uzay içinde bir dörtlüyanal Öklidyen düzlem içinde onun bir paralelkenar genelleme inşasıdır. Bu isim araştırmacı Tullio Levi-Civitaya ithafendir. Bir paralelkenar gibi, bir paralelkenarımsının iki zıt yüzleri AA′ ve BB′ paralel düz olmasına rağmen, ancak dördüncü kenar A′B′ değil, genel olarak, paralel ya da AB kenarı boyunca aynı uzunlukta olacaktır.
Ayrık diferansiyel geometri diferansiyel geometri içindeki kavramların ayrık karşılıklarının çalışmasıdır. Bunun yerine düzgün eğriler ve yüzeyler, burada çokgenler, örgüler ve yalın karmaşıklıklardır. Bu bilgisayar grafikleri ve topolojik kombinatoriklerin çalışması içinde kullanılabilir.
Bu diferansiyel geometri konuların bir listesidir. Ve aynı zamanda Lie grubu konularının listesi metrik geometri ve diferansiyelin sözlüğü bkz.
Klasik diferansiyel geometride, geliştirme öklid uzayı üzerinde başka bir düzgün yüzeyin yuvarlanmasının basit fikrini ifade eder. Örneğin, bir noktada, yüzeyine teğet düzlemin diğer noktalarında tanjant yüzey elde etmek için yüzeyi etrafında haddelenebilir. Birbiri üzerine haddelenen yüzeyleri arasındaki temas teğet iki yüzey üzerindeki noktalar arasındaki bir ilişki sağlar. Bu ilişki örten yüzeyler arasında tanımlanmış ise, o zaman iki yüzeylerin birbiri ya da birbirlerinin gelişmeleri geliştirilebilir olduğu söylenmektedir. Diğer bir deyişle, yerel bir izometri, iki yüzey arasında yazışmaları sağlar. Yüzeylerinden biri bir düzlem ise, özellikle, daha sonra diğer bir geliştirilebilir yüzey olarak adlandırılır: geliştirilebilir, böylece yüzey düzlemine yerel olarak izometrik olan bir bileşendir. Silindir geliştirilebilir, ama küre değil.
Kapalı zamansı eğri (KZE), matematiksel fizikte, “kapalı” uzayzamanda, başlangıç noktasına geri dönen bir parçacığın Lorentz manifoldundaki zaman çizgisidir. Bu olasılık ilk defa, genel göreliliğin eşitsizliklerine uygun bir çözüm keşfetmiş olan Kurt Gödel tarafından 1949 yılında ortaya çıkartılmıştır. Gödel, KZElerin aynı zamanda Gödel ölçüsü olarak bilinmesini sağlamıştır ve o zamandan beri de Tipler silindiri ve geçilebilir solucandelikleri gibi KZEleri içeren başka genel rölativite çözümleri bulunmuştur. Eğer KZEler varsa, varlıkları geriye doğru zaman yolculuğunun en azından kuramsal olarak olası olduğuna kanıt olarak sunulabilir, bu da dede paradoksu kaygısını ortaya çıkartabilir, ancak Novikov öztutarlılık ilkeleri bu biçim paradokslardan kaçınılabileceğini belirtmektedir. Bazı fizikçiler, belirli genel görelilik çözümlerinde yer alan KZElerin, ileride ortaya atılacak ve genel göreliliğin yerine geçecek olan kuantum kütleçekimi kuramıyla denklemden atılabileceğini savunmaktadır, Stephen Hawking bu görüşü kronoloji korunumu varsayımı olarak adlandırmıştır. Diğerleri ise, belirli bir uzayzamandaki tüm kapalı zamansı eğrilerin aynı olay ufkundan geçmesi durumunda –ki bu da kronojik sansür olarak isimlendirilebilecek bir özelliktir–; bu uzayzaman tüm olay ufuklarından temizlense dahi, yine de düzgün nedensellikte davranacağını ve bir gözlemcinin nedensellik ihlalini belirleyemeyeceğini savunmaktadırlar.
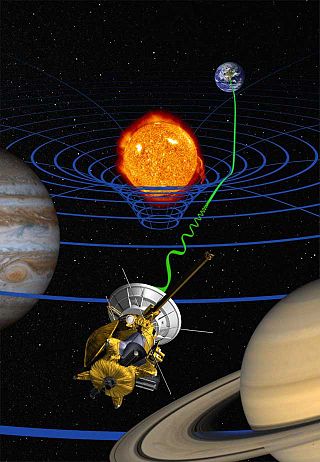
Genel görelilik veya genel izafiyet, 1907 ve 1915 yılları arasında Albert Einstein tarafından geliştirilen bir çekim teorisidir. Genel göreliliğe göre, kütleler arasında gözlenen kütleçekim etkisi uzayzamanın eğrilmesinden kaynaklanır.
On dokuzuncu yüzyıldan beri, bazı fizikçiler doğanın temel kuvvetlerini dikkate alan tek bir kuramsal çerçeve geliştirmeye çabaladılar: birleşik alan teorisi. Klasik birleşik alan teorileri, klasik fizik temelinde bir birleşik alan teorisi yaratmaya çalıştı. Bir kısım fizikçi ve matematikçi tarafından, Birinci ve İkinci Dünya Savaşları arasındaki yıllarda, özellikle yerçekimi ve elektromanyetizmin birleştirilmesi konusunun hararetle peşinden koşuldu. Bu çalışmalar, diferansiyel geometrinin saf bir matematiksel gelişim olarak ortaya çıkmasını teşvik etti. Albert Einstein klasik birleşik alan teorisini geliştirmeye çabalayan pek çok fizikçi arasında en tanınmışıdır.

Matematikte Riemann küresi, genişletilmiş karmaşık düzlemin artı sonsuzdaki noktanın bir modelidir. Carl Friedrich Gauss tarafından daha önceden düşünülmüş olsa da, öğrencisi Bernhard Riemann'ın adıyla anılmaktadır. Genişletilmiş bu düzlem, genişletilmiş karmaşık sayıları—yani artı sonsuzdaki ∞ değerli karmaşık sayıları—temsil eder. Riemann modelinde, "0" noktası çok küçük sayılara yakın olur ise "∞" noktası çok daha büyük sayılara yakınlaşır.

Matematikte Riemann yüzeyi, özellikle karmaşık analizde bahsi geçen tek boyutlu karmaşık bir manifolddur. Bu yüzey(ler) ilk olarak Bernhard Riemann tarafından incelenmiş ve isimlendirilmiş. Riemann yüzeyleri, karmaşık düzlemin deforme olmuş versiyonları olarak düşünülebilir: her noktanın yakınında karmaşık düzlemin yerel olarak yamaları gibi görünürler, ama topolojisi oldukça farklı olabilmektedir.

Élie Joseph Cartan, ForMemRS Lie grupları, diferansiyel sistemler ve diferansiyel geometri teorisinde temel çalışmalar yapan etkili bir Fransız matematikçi. Ayrıca genel göreliliğe ve dolaylı olarak kuantum mekaniğine önemli katkılarda bulundu. Yirminci yüzyılın en büyük matematikçilerinden biri olarak kabul edilmektedir.
Matematikte, integral geometri, belirli bir uzayın simetri grubu altındaki geometrik uzay değişmezi üzerindeki ölçü teorisidir. Daha yakın zamanlarda, anlam, bir geometrik uzaydaki fonksiyon uzayından başka bir geometrik uzaydaki fonksiyon uzayına değişmeyen dönüşümlerin bir görünümünü içerecek şekilde genişletildi. Bu tür dönüşümler genellikle Radon dönüşümü ve genellemeleri gibi integral dönüşümlerin biçimini alır.
Matematik tarihi ile bağlantılı olarak, İtalyan cebirsel geometri okulu, özellikle cebirsel yüzeylerde olmak üzere birasyonel geometride uluslararası olarak yapılan yarım yüzyıldan fazla süreci içeren birçok çalışmaya atıfta bulunmaktadır. Bölgede, önemli katkılarda bulunan önde gelen 30-40 matematikçi vardı ve bunların yaklaşık yarısı aslında İtalyandı. Liderlik Roma'da Guido Castelnuovo, Federigo Enriques ve Francesco Severi'nin en derin keşiflerinden bazılarına dahil olan ve aynı zamanda tarzı belirleyen gruba düştü.

Geometri, şekil, boyut, şekillerin göreceli konumu ve uzayın özellikleri ile ilgili sorularla ilgilenen bir matematik dalıdır. Geometri, en eski matematiksel bilimlerden biridir.

















