
Olasılık kuramı ve istatistikte, beta dağılımı, [0,1] aralığında iki tane pozitif şekil parametresi ile ifade edilmiş bir sürekli olasılık dağılımları ailesidir. Çok değişkenli genellemesi Dirichlet dağılımıdır.

Olasılık kuramı ve istatistik bilim dallarında gamma dağılımı iki parametreli bir sürekli olasılık dağılımıdır. Bu parametrelerden biri ölçek parametresi θ; diğeri ise şekil parametresi k olarak anılır. Eğer k tam sayı ise, gamma dağılımı k tane üstel dağılım gösteren rassal değişkenlerin toplamını temsil eder; rassal değişkenlerin her biri nin üstel dağılımı için parametre  olur.
olur.

Çevrel çember, geometride, bir çokgenin tüm köşelerinden geçen çember. Bu çemberin merkezi çevrel özek olarak isimlendirilir.

Brocard noktaları, geometride bir üçgen içinde yer alan özel noktalardır. Fransız matematikçi Henri Brocard'ın çalışmalarından dolayı bu adı almıştır.
Fizikte, Lorentz dönüşümü adını Hollandalı fizikçi Hendrik Lorentz'den almıştır. Lorentz ve diğerlerinin referans çerçevesinden bağımsız ışık hızının nasıl gözlemleneceğini açıklama ve elektromanyetizma yasalarının simetrisini anlama girişimlerinin sonucudur. Lorentz dönüşümü, özel görelilik ile uyum içerisindedir. Ancak özel görelilikten daha önce ortaya atılmıştır.
Doğrusal cebirde veya daha genel ifade ile matematikte matris çarpımı, bir matris çiftinde yapılan ve başka bir matris üreten ikili işlemdir. Reel veya karmaşık sayılar gibi sayılarda temel aritmetiğe uygun olarak çarpma yapılabilir. Başka bir ifade ile matrisler, sayı dizileridir. Bu yüzden, matris çarpımını ifade eden tek bir yöntem yoktur. "Matris çarpımı" terimi çoğunlukla, matris çarpımının farklı yöntemlerini ifade eder. Matris çarpımının anahtar özellikleri şunlardır: Asıl matrislerin satır ve sütun sayıları, ve matrislerin girişlerinin nasıl yeni bir matris oluşturacağıdır.

Geometride, Thales teoremi, A, B ve C, AC çizgisinin bir çap olduğu bir daire üzerinde farklı noktalar ise, ∠ABC açısının bir dik açı olduğunu belirtir. Thales teoremi, çevre açı teoreminin özel bir durumudur ve Öklid'in Elemanlar adlı eserinin üçüncü kitabında 31. önermenin bir parçası olarak bahsedilmiş ve kanıtlanmıştır. Genellikle, teoremin keşif için şükran kurbanı olarak bir öküz sunduğu söylenen Miletli Thales'e atfedilir, ancak bazen Pisagor'a da atfedilir.
Özel fonksiyonların önemli bir bölümünü oluşturan hipergeometrik fonksiyonlar matematik, fizik, mühendislik ve olasılıkta karşımıza çıkar.

Smith abağı veya Smith diyagramı, radyo ve mikrodalga frekanslarındaki iletim hatlarının tasarımı ve empedans eşlemesinde kullanılan bir grafiktir. Elektrik-elektronik ve haberleşme mühendisleri tarafından kullanılan bu abak Phillip H. Smith (1905–1987) tarafından icat edilmiştir. Smith abağı aynı anda empedans, admitans, yansıma ile saçılma katsayıları, kazanç konturu ve stabilite gibi çok sayıda parametreyi aynı anda gösterebilmektedir; bu yüksek frekans devreleri dışında mekanik titreşim analizinde de kullanılmasını sağlamıştır. Smith abağı genelde birim yarıçap içinde kullanılır; buna karşın abağın geri kalanı da elektronik osilatör ve stabilite analizinde kullanılmaktadır.

Geometride açıortay teoremi, bir üçgenin kenarının karşı açıyı ikiye bölen bir çizgiyle bölündüğü iki parçanın göreli uzunluklarıyla ilgilidir. Göreli uzunluklarını, üçgenin diğer iki kenarının göreli uzunluklarına eşitler.

Öklid geometrisinde, Batlamyus teoremi, bir kirişler dörtgeninin dört kenarı ile iki köşegeni arasındaki bir ilişkiyi gösteridir. Teorem, Yunan astronom ve matematikçi Batlamyus'un adını almıştır. Batlamyus, teoremi astronomiye uyguladığı trigonometrik bir tablo olan kirişler tablosunu oluşturmaya yardımcı olarak kullandı.
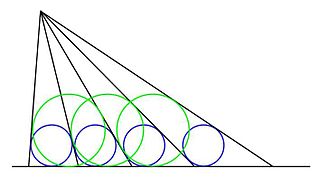
Geometride, eş iç teğet çemberler teoremi bir Japon Sangaku'sundan türetilir ve aşağıdaki yapıya ilişkindir: belirli bir noktadan belirli bir çizgiye bir dizi ışın çizilir, öyle ki bitişik ışınlar ve taban çizgisi tarafından oluşturulan üçgenlerin iç teğet çemberleri eşittir. Çizimde eş mavi çemberler, açıklandığı gibi ışınlar arasındaki mesafeyi tanımlar.

Üçgen geometrisinde, üçgenin iç çemberi ve dokuz nokta çemberi, üçgenin Feuerbach noktasında birbirine içten teğettir. Feuerbach noktası bir üçgen merkezidir, yani tanımı üçgenin yerleşimine ve ölçeğine bağlı değildir. Clark Kimberling'in Üçgen Merkezleri Ansiklopedisi'nde X(11) olarak listelenmiştir ve adını Alman geometrici Karl Wilhelm Feuerbach'tan almıştır.
Trigonometride, trigonometrik özdeşlikler trigonometrik fonksiyonları içeren ve eşitliğin her iki tarafının da tanımlandığı değişkenlerin her değeri için doğru olan eşitliklerdir. Geometrik olarak, bunlar bir veya daha fazla açının belirli fonksiyonlarını içeren özdeşliklerdir. Bunlar üçgen özdeşliklerinden farklıdır, bunlar potansiyel olarak açıları içeren ama aynı zamanda kenar uzunluklarını veya bir üçgenin diğer uzunluklarını da içeren özdeşliklerdir.

Trigonometride, kotanjant teoremi veya kotanjantlar yasası, bir üçgenin kenar uzunlukları ile üç iç açısının yarılarının kotanjantları arasındaki ilişkidir.

Trigonometride Mollweide formülü, bir üçgendeki kenarlar ve açılar arasındaki bir çift ilişkidir.

Pompeiu teoremi, Romanyalı matematikçi Dimitrie Pompeiu tarafından keşfedilen bir düzlem geometrisi sonucudur. Teorem basittir, ancak klasik değildir. Aşağıdakileri ifade eder:
- Bir eşkenar üçgen verildiğinde Düzlemde ABC ve ABC üçgeninin düzleminde bir P noktası, PA, PB ve PC uzunlukları bir üçgenin kenarlarını oluşturur.







































