Işık hızı
 Güneş ışığının, Güneş'in yüzeyinden Dünya'ya olan ortalama mesafeyi geçmesi yaklaşık 8 dakika 17 saniye sürer. | |
| Kesin değerler | |
|---|---|
| metre bölü saniye | 299792458 |
| Yaklaşık değerler (üç basamağa kadar) | |
| kilometre bölü saat | 1080000000 |
| mil bölü saniye | 186000 |
| mil bölü saat[1] | 671000000 |
| astronomik birim bölü gün | 173 |
| parsek bölü yıl | 0,307 |
| Işığın yaklaşık seyahat süreleri | |
| Mesafe | Zaman |
| bir fit | 1,0 ns |
| bir metre | 3,3 ns |
| sabit yörüngeden Dünya'ya | 119 ms |
| Dünya ekvatorunun uzunluğu | 134 ms |
| Ay'dan Dünya'ya | 1,3 sn |
| Güneş'ten Dünya'ya (1 AU) | 8,3 dk |
| bir ışık yılı | 1,0 yıl |
| bir parsek | 3,26 yıl |
| en yakın yıldızdan Güneş'e (1,3 pc) | 4,2 yıl |
| en yakın gökadadan (CMa Dwarf) Dünya'ya | 25.000 yıl |
| boydan boya Samanyolu | 100.000 yıl |
| Andromeda Gökadası'ndan Dünya'ya | 2,5 milyon yıl |
Işığın boşluktaki hızı, fiziğin birçok alanında kullanılan önemli bir fiziksel sabittir. Genellikle c sembolüyle gösterilir. Tam değeri saniyede 299.792.458 metredir (saniyede yaklaşık olarak 300.000 km; saatte 1.080.000.000 km olarak ifade edilir). Metrenin uzunluğu bu sabitten ve uluslararası zaman standardından hesaplanmıştır. Özel göreliliğe göre c, evrendeki bütün madde ve bilgilerin hareket edebileceği maksimum hızdır. Bütün kütlesiz parçacıkların ve ilgili alanlardaki değişimlerin boşluktaki hareket hızıdır (ışık ve çekimsel dalgalar gibi elektromanyetik radyasyon dahil). Bu parçacıklar ve dalgalar gözlemcinin eylemsiz referans çerçevesi ya da kaynağın hareketi ne olursa olsun c'de hareket ederler. Görelilik teorisi'nde c, uzay-zaman arasındaki ilişkiyi kurar; aynı zamanda meşhur kütle-enerji eşdeğerliliği formülünde de gözükür E = mc2.[2] Işığın hava veya cam gibi şeffaf maddelerdeki ilerleyiş hızı c'den azdır. Benzer şekilde radyo dalgalarının tel kablolardaki ilerleyişi de c'den yavaştır. Işığın madde içindeki hızı v ile c arasındaki orana o maddenin kırılma endeksi (c) denir (n = c / v). Örneğin, görülebilir ışık için camın kırılma endeksi genellikle 1,5 civarındadır. Yani ışık camın içinde c / 1,5 ≈ 200.000 km/s ile hareket eder. Hangi açıdan bakılırsa bakılsın ışık ve öteki elektromanyetik dalgalar anında yayılıyormuş gibi gözükür ancak, ölçülebilir hızlarının uzun mesafeler ve hassas ölçümlerle ölçülebilir sonuçları vardır. Uzaydaki keşif araçlarıyla iletişim kurarken mesajların Dünya'dan uzay aracına ya da uzay aracından Dünya'ya ulaşması dakikalar ya da saatler alabilir. Yıldızlardan gelen ışık onları yıllar önce terk etmiştir ve bu sayede uzaktaki nesnelere bakarak evrenin tarihini çalışma şansı verir. Işığın ölçülebilir hızı aynı zamanda bilgisayardaki bilgilerin çipler arasında aktarılması gerektiği için bilgisayarların teorik hızını da sınırlar. Işık hızı, uzak mesafeleri yüksek isabetle ölçebilmek için uçuş zamanı ölçümlerinde de kullanılır.
Ole Rømer ilk olarak 1676'da, Jüpiter'in uydusu Io'nun görünür hareketini inceleyerek, ışığın ölçülebilir bir hızda hareket ettiğini göstermiştir (anlık hareketin aksine). 1865'te James Clerk Maxwell Elektromanyetizma Teorisi'nde ışığın elektromanyetik bir dalga olduğunu ve bu nedenle c hızında hareket ettiğini ileri sürmüştür. 1905'te Albert Einstein ışığın hızının herhangi bir referans çerçevesinde ışık kaynağından bağımsız olduğunu öne sürmüştür ve bu varsayımının sonuçlarını görelilik teorisini öne atıp c parametresini ışık ve elektromanyetizma dışındaki şeylerle alakalı olduğunu göstermiştir.
Yüzyıllar boyunca süren ve giderek daha da kesinleşen ölçümler sonucunda 1975'te ışığın süratinin 299.792.458 m/s olduğu 4 milyarda birlik bir belirsizlikle hesaplanmıştır. 1983 yılında metre, Uluslararası Birimler Sistemiyle ışığın boşlukta 1/299.792.458 saniyede kat ettiği mesafe olarak yeniden tanımlanmıştır. Bunun sonucu olarak, c'nin değeri metrenin tanımı ile net bir şekilde sabitlenmiştir.[3]
Sayısal Değer, Formül ve Birimler
Işık hızı genellikle İngilizce "constant" ("sabit") ya da Latince "celerity" (hızlı, çabuk) kelimesinin ilk harfi olan “c” ile ifade edilir. Geçmişte "V" ışık hızı için alternatif bir sembol olarak kullanılmıştır ve 1865'te James Clerk Maxwell tarafından ortaya atılmıştır. 1856'da Wilhelm Eduard Weber ve Rudolf Kohlrausch c'yi daha sonra ışık hızının √2 katına denk geldiği görülen başka bir sabit için kullanmışlardır. 1894'te Paul Druder c'yi modern anlamıyla tekrar tanımlamıştır. Einstein Görecelik üzerine yazdığı Orijinal Almanca makalelerde V'yi kullanmıştır ama 1907'de o zaman ışık hızı için standart sembol haline gelmiş c'yi kullanmaya başlamıştır.[4][5]
Bazen c dalgaların herhangi bir maddesel çevredeki hızını ifade etmek için kullanılır ve c0 da ışığın boşluktaki hızını ifade etmek için kullanılır.[6] SI tarafından da kabul edilmiş bu alt indisli ifade diğer alakalı sabitlerle aynı forma sahiptir, μ0 vakum geçirgenliği veya manyetik sabit, ε0 boşluktaki iletkenlik veya elektrik sabiti ve Z0 uzayın direnci için.
1983'ten beri metre Uluslararası Ünite Sistemi'nde ışığın 1/299792458 saniyede kat ettiği mesafe olarak tanımlanmıştır. Bu tanım ışığın boşluktaki hızını kesin olarak 299792458 m/s olarak sabitlemiştir. Boyutsal fiziksel bir sabit olarak c ünite sistemlerinde farklı değerlere sahiptir. Fiziğin c'nin sıkça gözüktüğü görecelik gibi bölümlerinde, doğal ölçüm ünitesi ya da geometrik ölçüm ünitesi olarak c=1 kullanılır. Bu üniterler kullanıldığında c, 1 bölme ve çarpma işlemlerinde etkisiz olduğu için çok gözükmez.
Fizikteki Temel Rolü
Işığın boşluktaki yayılma hızı ışık kaynağının hareketinden de gözlemcinin hareketsiz referans noktasından da bağımsızdır. Işık hızının değişmezliği, 1905'te Maxwell'in Elektromanyetizma Teorisi'nden ve Luminiferous Aether(19. yüzyılda ışık kaynağı olduğu düşünülen teori)'ın varlığına dair bir kanıt olmamasından ilham alarak, Einstein tarafından öne sürülmüştür ve o zamandan bu yana birçok deney tarafından kanıtlanmıştır. Yalnızca iki yönlü ışığın(ışık kaynağın ve ayna gibi) hızının çevreden bağımsız olduğunu onaylamak mümkündür çünkü kaynakla alıcıdaki saatlerin nasıl senkronize edileceğine dair bir yol bulmadan ışığın tek yönlü hızını ölçmek mümkün değildir. Ancak, Einstein senkronizasyonunu saatlere uyguladığımızda tek yönlü ve çift yönlü ışık hızları birbirine eşitlenir. İzafiyet Teorisi bu değişimsizliğin sonuçlarını tüm eylemsiz referans çerçevelerinde fiziğin kanunlarının aynı olduğunu varsayarak inceler. Tek sonuç, c'nin bütün kütlesiz parçacıkların ve dalgaların, ışık dahil, boşluktaki hızıdır..

Özel göreliliğin birçok mantığa aykırı ve deneylerle onaylanmış çıkarımları vardır. Bunlara kütle-enerji denkliği (E = mc2),yükseklik kısalması(hareket eden cisimler kısalır) ve zaman genişlemesi (hareket eden saatler daha yavaş işler) dahildir. Boyun kısaldığı ve zamanın genişlediği γ etmeni Lorentz Faktörü olarak bilinir ve γ = (1 − v2/c2)−1/2 ile ifade edilir (v nesnenin hızı). γ ile 1 arasındaki fark günlük hızlar gibi c'den çok daha düşük olan hızlar için (özel göreliliğin Galilean göreliliği tarafından yaklaşıldığı bir durum) göz ardı edilebilir ancak göreceli bir hızla yükselir ve v c'ye yaklaştıkça sonsuzluğa doğru sapar.
Özel göreliliğin sonuçları uzay ve zamanı uzay-zaman olarak bilinen ve matematiksel formülü c parametresini içeren Lorentz değişmezi adlı özel bir simetriyi sağlayan bir yapı olarak kabul edilerek özetlenebilir. (c uzay ve zamanın birimlerine bağlıdır). Lorentz değişmezi modern fizik teorileri için neredeyse evrensel olarak kabul edilmiş bir çıkarımdır. Modern fizikte c hemen hemen her yerde ortaya çıkan, ışıkla alakası olmayan birçok konuda dahi görülen bir parametre haline gelmiştir. Örneğin, genel görelilik c'nin aynı zamanda yer çekiminin ve yer çekimsel dalgaların da hızı olduğunu tahmin etmektedir. Hareketsiz referans çerçevelerinde ışığın hızı sabit ve c'ye eşittir ancak ışığın ölçülebilir mesafedeki hızı mesafenin ve zamanın nasıl tanımlandığına bağlı olarak c'den farklı çıkabilir.[7]
Genel olarak c gibi temel sabitlerin uzay-zamanda değişmediği, yani mekana bağlı olmadığı ve zamanla değişmediği varsayılır. Ancak, değişik teorilerde ışığın hızının zaman içinde değişmiş olabileceği öne sürülmüştür. Bu değişimleri onaylayacak bir kanıt henüz bulunamasa da araştırmalar devam etmektedir. .[8][9]
Aynı zamanda genel olarak ışığın izotopik olduğu varsayılır. Yani, ne yönde ölçülürse ölçülsün aynı değere sahiptir. Nükleer enerji seviyelerinin yayılan çekirdeklerin ve optik rezonatörlerin fonksiyonu olarak gözlemleri olası iki taraflı eş yönsüzlüğe sıkı bir limit koymaktadır..[10][11]
Hızın üst limiti
Özel göreliliğe göre m kütleli ve v hızlı bir nesnenin enerjisi γmc2 ile ifade edilir. v 0 olduğunda γ 1'dir ve bu meşhur E = mc2 denklemini sağlar. v c'ye yaklaştıkça γ sonsuza yaklaşır ve kütlesi olan ve ışık hızında hareket eden bir nesneyi hızlandırmak sonsuz ölçüde bir enerji gerektirir. Kütlesi olan nesneler için ışık hızı üst hız limitidir ve fotonlar ışık hızından daha hızlı hareket edemezler. Bu birçok göreceli enerji ve momentum deneylerinde kanıtlanmıştır. .[12]

Daha genel olarak, bilginin ya da enerjinin c'den daha hızlı hareket etmesi imkânsızdır. Bunun bir argümanı, özel göreliliğin eş zamanlılık göreliliği olarak bilinen mantık dışı bir çıkarımını takip eder. Eğer A ve B olayları arasındaki mesafe, aralarındaki zaman aralığının c ile çarpımından büyükse, aralarında A'nın B'yi takip ettiği ya da B'nin A'yı takip ettiği referans çerçeveleri vardır ve bazılarında A ve B eş zamanlıdır. Bunun sonucu olarak, eğer bir şey hareketsiz bir referans çerçevesine göre c'den daha hızlı hareket ediyorsa başka bir çerçeveye göre zamanda geriye doğru hareket ediyor olur ve nedensellik bozulmuş olur. Böyle bir bir referans çerçevesinde bir etki nedeninden önce gerçekleşebilir. Nedenselliğin bu şekilde bozulması henüz kayıtlara geçmemiştir.[13]
Işıktan hızlı deneyler ve gözlemler
Bazı durumlarda enerji, cisimler ya da bilgi ışıktan hızlı hareket ediyormuş gibi gözükse de etmezler. Örneğin; aşağıdaki "ışığın bir çevrede yayılmasında'' bazı dalgaların hızı c'yi geçebilir. Örneğin, x-ray ışınlarının çoğu camdaki faz hızı c'yi geçmektedir ancak faz hızı dalgaların bilgiyi yayma hızını göstermez.[14]
Eğer bir lazer ışını uzaktaki bir nesne üzerinde hızlıca gezdirilir ise, ışık noktasının ilk hareketi ışığın uzaktaki nesneye ulaşma süresi nedeniyle gecikse de, ışık noktası c'den hızlı hareket edebilir. Ancak, yalnızca hareket eden fiziksel varlıklar lazer ve onun yaydığı ışıktır ve lazerden değişik noktalara ışık hızında hareket ederler. Benzer olarak, uzaktaki bir gölge de zamanda bir gecikmeden sonra ışıktan hızlı hareket ettirilebilir. İki durumda da herhangi bir madde, enerji ya da bilgi ışıktan hızlı hareket etmez.[15]
Hareket eden iki referans çerçevesi arasındaki mesafenin değişme oranı c'nin üzerinde bir değere sahip olabilir. Ancak, bu hareketsiz bir çerçeve içinde ölçülen herhangi bir cismin hızını yansıtmaz.[15]
Bazı kuantum etkileri, EPR paradoksunda olduğu gibi, anında, yani c'den hızlı olarak aktarılıyormuş gibi gözükebilir. Bir örnek birbirine girmiş iki parçacığın kuantum durumlarını içermektedir. İki parçacıktan herhangi biri incelenene kadar parçacıklar üst üste gelmiş iki kuantum durumu içinde var olurlar. Eğer parçacıklar ayrılıp birinin kuantum durumu incelenirse ötekinin kuantum durumu anında belirlenmiş olur. Ancak, ilk parçacığın gözlemlendiğinde hangi kuantum durumunu kontrol etmek mümkün olmadığı için bilgi bu yolla yayılamaz.[15][16]
Işıktan hızlı hızları tahmin eden başka bir kuantum etkisi de'' Hartman Etkisi''dir. Belirli koşullar altında, yapay bir parçacığın bir bariyerden geçmesi için gereken zaman, bariyerin kalınlığı ne olursa olsun, sabittir. Bu, yapay parçacığın geniş bir boşluğu ışıktan hızlı bir şekilde geçmesiyle sonuçlanabilir. Ancak, bu etki kullanılarak herhangi bir bilgi gönderilemez.[17]
Sözde ışıktan hızlı hareket, radyo-galaksilerin göreceli jetleri, yıldızımsı gök cisimleri gibi astronomik nesnelerde gözlemlenebilir. Ancak, bu jetler ışıktan hızlı hareket etmemektedir. Göze ışıktan hızlı gelen hareket cismin ışık hızına yaklaşmasının ve dünyaya düşük bir görüş açısıyla yaklaşmasının sonucudur.[18]
Genişleyen evrenin modellerinde galaksiler ne kadar uzaklarsa birbirlerinden o kadar hızlı uzaklaşırlar. Ayrılma uzaydaki hareketin değil, uzayın genişlemesinin sonucudur. Örneğin, dünyaya uzak olan galaksiler dünyaya olan uzaklarıyla orantısal bir hızla uzaklaşırlar.[19]
Işığın yayılımı
Klasik fizikte ışık elektromanyetik dalga olarak sınıflandırılmıştır. Elektromanyetik alanların klasik hareketi Maxwell denklemleriyle tanımlanmıştır. Bu denklemlerde, elektromanyetik dalgaların boşluktaki yayılma hızı olan c elektrik sabite ve manyetik sabite c = 1/√ε0μ0.[20] Modern kuantum fizikte elektromanyetik alan kuantum elektrodinamik teorisiyle (QED) tanımlanmaktadır. Bu teoride ışık, elektromanyetik alanın temel çıkışı olan fotonlarla tanımlanır. QED'ye göre fotonlar kütlesiz parçacıklardır ve boşlukta ışık hızıyla hareket ederler.QED'nin fotonun kütleye sahip olduğu genişlemeleri de düşünülmüştür. Böyle bir teoride fotonun hızı frekansına bağlı olur ve değişmez c hızı ışığın boşluktaki hızının üst limiti olur. Işığın hızında testlerde herhangi bir değişim gözlenmemiştir ve bu da fotonun kütlesine sıkı bir limit koymaktadır. Elde edilen limit kullanılan modele göre değişebilir.
Işığın hızının frekansına bağlı olarak değişmesinin başka bir sebebi de, kuantum yerçekimindeki bazı teorilerde tahmin edildiği gibi, özel göreliliğin gelişigüzel küçüklükteki durumlarda uygulanamaması olabilir. 2009'da gamma ışını patlaması GB 090510'un gözlemlerinde farklı enerjilerdeki fotonların hızında bir değişme gözlemlenmemiştir, bu da Lorentz değişmezinin en azından Planck Uzunluğu' nun 1.2'ye bölümüne kadar onaylanması demektir.[21]
Ortam İçinde
Bir çevrede ışık genel olarak c'ye eşit bir hızda yayılmaz; daha da fazlası, değişik ışık dalgaları değişik hızlarda ilerleyebilir. Düz bir dalganın (bir frekansla bütün uzayı doldurabilen dalga) tavan ve taban yaparak yayıldığı hıza faz hızı denir. Ölçülebilir bir uzunluğu(ışık nabzı) olan gerçek bir fiziksel işaret farklı bir hızda ilerler. Nabzın en büyük bölümü grup hızında ilerlerken erken kısımları ön hızla ilerler.
Faz hızı ışın bir maddede ya da bir maddeden ötekine nasıl ilerlediğini belirlerken önemlidir. Kırılma endeksi olarak temsil edilir. Bir maddenin kırılma endeksi, c' nin maddedeki faz hızına oranı olarak tanımlanır. Bir maddenin kırılma endeksi ışığın frekansına, yoğunluğuna, polarizasyonuna ya da yayılma yönüne bağlı olabilir ama çoğu durumlarda maddeye bağlı bir sabit olarak görülebilir. Havanın kırılma endeksi yaklaşık olarak 1.0003'tür. Bose- Einstein Yoğuşuğu gibi egzotik maddelerde kırılma endeksi sıfıra yakın olabilir, bu da ışığın hızını saniyede yalnızca birkaç metreye kadar düşürebilir. Ancak, bu atomlar arasındaki emilim ve tekrar yayılma gecikmesini temsil eder. Maddedeki ışığın yavaşlamasına aşırı bir örnek olarak; iki bağımsız fizikçi ekibi, ışığı rubidyum elementinin Bose-Einstein yoğunlaşmasından geçirerek "tamamen durma" noktasına getirdiklerini iddia ettiler. Ancak bu deneylerdeki "ışığın durması" tanımı yalnızca ışığın atomun daha kararsız hallerinde depolanması ve daha sonra gelişigüzel bir zamanda tekrar yayılması şeklinde olmuştur. "Durduğu" sürede ışık olmayı bırakmıştır. Bu tür bir davranış, genellikle ışık hızını "yavaşlatan" tüm saydam ortamlar için mikroskobik olarak doğrudur.[22]
Saydam maddelerde kırılma endeksi genelde 1'den büyüktür, yani faz hızı c' den küçüktür. Öteki materyallerde kırılma endeksinin bazı frekanslarda 1'den küçük olması olasıdır; bazı egzotik maddelerde kırılma endeksinin negatif olması dahi olasıdır. Nedenselliğin bozulmaması gereksinimi herhangi bir maddenin dielektrik sabitinin gerçek ve sanal kısımlarının Kremars- Kronig ilişkisiyle bağlı olduğunu ima eder. Pratik olarak, kırılma endeksinin 1'den küçük olduğu maddelerde dalganın emilimi o kadar hızlıdır ki c' den daha hızlı bir sinyal gönderilemez.
Farklı grup ve faz hızları olan bir nabız zaman içinde biter. Bu süreç ayrılım olarak bilinir. Bazı maddeler ışık dalgaları için çok düşük grup hızlarına sahiptir, yavaş ışık olarak adlandırılan ve deneylerle onaylanmış bir fenomen. Tam tersi, c'yi aşan grup hızları, aynı zamanda deneylerde gözlemlenmiştir. Anlık ya da zamanda geriye doğru hareket eden nabızlar için grup hızın sonsuz olması ya da negatif çıkması da mümkün olmalıdır.[23]
Ancak, bu seçeneklerin hiçbiri bilginin c'den daha hızlı aktarılmasını sağlamaz. Erken kısımlarından daha hızlı bir nabızla bilgi yollamak mümkün değildir.[23]
Bir parçacığın bir maddenin içinde o maddenin faz hızından daha hızlı ilerlemesi mümkündür. Yüklü bir parçacık bunu iletken olmayan bir maddenin içinde yaptığı zaman Cherenkov Radyasyonu olarak bilinen bir şok dalgası yayılır. .[24]
Ölçülebilirliğin pratik etkileri
Işık hızı iletişimle alakalıdır: Tek yönlü ve gidiş-geliş gecikmeleri sıfırdan büyüktür. Bu küçükten astronomik ölçülere kadar geçerlidir. Öteki yandan, mesafe ölçümü gibi bazı teknikler ışığın ölçülebilir hızına da bağlı olabilir.
Küçük ölçekler
Süper bilgisayarda, ışık hızı bilgilerin işlemciler arasında ne kadar hızlı yollanabileceğine dair bir sınır oluştumaktadır. Eğer bir işlemci 1 gigahertz'den açılıyorsa bir sinyal bir döngüde maksimum 30 cm ilerleyebilir. Bu yüzden işlemciler iletim gecikmesini minimuma indirmek için birbirilerine yakın konmalıdırlar, bu da soğutma sorunlarına neden olabilir. Eğer saat frekansları yükselmeye devam ederse ışık hızı tekil çiplerin tasarımında bir limit haline gelecektir.[25]
Dünya üzerinde büyük mesafeler
Örneğin, dünyanın 40075 km ve c' nin de 300000 km/s civarında olduğunu düşünürsek bilginin kürenin yarısını gezeceği en kısa süre 67 milisaniyedir. Işık dünyada optik bir iplikte gezerken iletim süresi daha uzundur çünkü kırılma endeksine bağlı olarak ışık optik iplikte %35 civarında daha yavaş hareket eder. Ayrıca düz hatlar global iletişimlerde nadiren kullanılır ve sinyal elektronik düğmeden ya da sinyal üreticiden geçerken yavaşlar.[26]
Uzay uçuşları ve astronomi

Benzer şekilde dünya ve uzay araçları arasındaki iletişim de anlık değildir. Kaynakla alıcı arasındaki mesafe arttıkça daha da belirginleşen bir gecikme vardır. Apollo 8 ayın yörüngesine giren ilk insanlı hava aracı olduğunda bu gecikme çok büyüktü: Her sorunun cevabı için yer kontrol istasyonu 3 saniye beklemek zorundaydı. Dünya ve Mars arasındaki gecikme 5-20 dakika arası değişebilir.
NASA Jüpiter'in yörüngesinde dolaşan bir probedan bilgi almak için saatlerce beklemek zorundadır. Bu da bir navigasyon hatası durumunda düzeltmenin zamanında yetişememesi riskini ortaya çıkarmaktadır.
Daha uzaktaki astronomik kaynaklardan ışık ya da farklı sinyaller almak bundan da uzun sürebilir. Uzak nesnelerin ışığın ölçülebilir hızı nedeniyle daha genç gözükmeleri astronomlara yıldızlarsın, galaksilerin hatta evrenin evrimini gözlemleme şansı vermiştir.
Bazen astronomik mesafeler, özellikle popüler bilim yayınlarında ve medyada ışık yılıyla ifade edilir. Işık yılı ışığın bir yılda kat ettiği mesafedir. Yaklaşık olarak bir ışık yılı 10 trilyon km ya da 6 trilyon mildir. Dünyaya güneşten sonraki en yakın yıldız yaklaşık 4,2 ışık yılı uzaklıktadır.[27]
Mesafe ölçümü
Radyo sistemleri bir hedefe olan mesafeyi radyo dalgasının antenden yansıtıldıktan sonra hedeften dönmesinin aldığı zamana göre ölçer. Global pozisyonlama sistemi (GPS) alıcısı GPS uydusuna olan uzaklığını uydulardan gelen sinyallerin süresine göre hesaplar ve uydularla arasındaki mesafeden kendi yerini hesaplar. Lunar Lazer Menzilleme deneyi, radar astronomisi ve Derin Uzay Ağı Ay'a, gezegenlere ve uzay araçlarına olan mesafeleri sinyallerin gidiş-geliş sürelerine göre hesaplarlar.
Yüksek frekanslı alım satım
Işık hızı yüksek frekanslı alım-satımda giderek daha önemli hale gelmektedir. Tüccarlar mallarını birkaç saniye önce teslim ederek dakika avantajı sağlamaya çalışmaktadır. Örneğin; tüccarlar mikrodalga iletişimi optik-fiber iletişime tercih ediyorlar çünkü optik-fiber sinyaller ışıktan %30-40 daha yavaş hareket ederken mikrodalgalar havada ışık hızına yakın hızlarda hareket ederler.[28]
Ölçüm
c'nin değerini belirlemenin farklı yolları vardır. Bir yol, ışığın yayıldığı gerçek hızı hesaplamaktır ki değişik astronomik ve dünya temelli adımlarla yapılabilir. Ancak ε0 ve μ0 gibi fiziksel değerlerin c ile bağlantısı kurularak da hesaplanabilir. Tarihte en isabetli ölçümler, ışığın dalga boyu ve frekansı tek tek hesaplanıp sonuçlar c' ye eşitlenerek elde edilmiştir.
Astronomik ölçümler

Dış uzay, büyük boyutu ve mükemmele yakın boyutu sayesinde c'yi ölçmek için son derece elverişlidir. Tipik olarak, birisi ışığın belirli bir referans sistemindeki mesafeyi katetmesi için gerek zamanı ölçer. Tarihte bu tip ölçümler, referans uzaklığın dünya temelli birimlerle ne kadar isabetli olarak ölçüldüğüne göre, son derece isabetli olarak yapılabilmiştir. Elde edilen sonuçlar gün başına Astronomik Birimlerle (AU) ifade edilir.
Ole Christensen Romer astronomik ölçümleri kullanarak ışığın miktarsal hızının ilk tahminlerini yapmıştır. Dünyadan ölçüldüğü zaman uyduların gezegenlerin etrafında dönme hızı dünya gezegenlere yaklaşırken, uzaklaşırken ki hızlarından daha fazladır. ışığın gezegenden dünyaya katettiği mesafe, dünya yörüngesinde o gezegene en yakın konumundayken daha kısadır, mesafedeki fark dünyanın Güneş etrafındaki yörüngesinin çapıdır. Uydunun periyodundaki değişim ışığın uzak ya da yakın mesafeyi katetmesindeki zaman farkından oluşmaktadır.
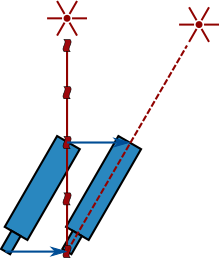
Bir başka metotsa 18. yüzyılda James Bradley tarafından keşfedilen "ışığın sapması"dır. Bu etki, uzaktaki bir kaynaktan ulaşan ışığın hızına gözlemcinin hızının vektör olarak eklenmesiyle oluşur. Hareketli bir gözlemci ışığı farklı bir noktadan gelirken gözlemler ve kaynağın yerini farklı görür. Dünya Güneş'in etrafında döndükçe dünyanın hızının yönü değiştiği için bu yıldızların hareket ettiği izlenimi verir. Yıldızların konumunun açısal farkından ışığın hızını dünyanın güneş etrafındaki hızı cinsinden yazmak mümkündür. 1729'da Bradley bu metodu kullanarak ışığın dünyanın yörüngedeki hızından 10,210 kat daha hızlı hareket ettiğini öne sürmüştür.[29]
Astronomik Birim
AU yaklaşık olarak dünya ile güneş arasındaki mesafedir. 2012'de net olarak 149 597 870 700 m. olarak yeniden tanımlanmıştır. Daha önce AU SI birimleri ile değil, Güneş tarafından uygulanan yerçekimi kuvvetinin klasik mekanik çerçevesindeki koşullarıyla ifade edilmiştir. Güncel tanım, AU'nun önceki tanımının tavsiye edilen şekilde metre ile ifade edilmiş halini kullanmaktadır. Bu yeniden tanımlama, ışık hızını saniye başına AU'da sabitlemiştir.
Daha önce c' nin tersi saniyede AU olarak ifade edilmiş ve radyo sinyallerinin Güneş Sistemin'deki araçlara ulaştığı zaman kullanılarak hesaplanmıştır. Bu tarz birçok hesaplama birleştirilerek birim uzaklık başına ışık zamanı için en iyi değer elde edilebilir. Örneğin; 2009'da Uluslararası Astronomik Birlik tarafından kabul edilen en iyi tahmin:[30][31]
- Birim uzaklık başına ışık zamanı: 7002499004783836000♠499.004783836(10) s
- c = 7008299792457999999♠0.00200398880410(4) AU/s = 7002173144632674000♠173.144632674(3) AU/day.
Bu hesaplardaki göreceli hesap hatası milyarda 0,02' dir. Metre belli bir zamanda ışık tarafından katedilen mesafe olarak tanımlandığı için, ışık zamanının önceki AU tanımı ile ölçülmesi eski AU' nun metre ile ölçülmesi olarak yorumlanabilir.[Note 7]
Uçuş zamanı teknikleri

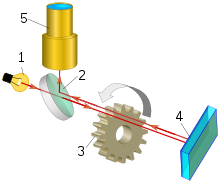
Işık hızını ölçmenin bir metodu da ışığın bilinen bir noktadaki bir aynaya gitme ve geri dönme hızının hesaplanmasıdır. Bu Fizeau-Foucault düzeneğinin arkasındaki prensiptir ve Hippolyte Fizeau ve Leon Foucault tarafından geliştirilmiştir.
Fizeu tarafından kullanılan bu düzenek 8 kilometre uzaklıktaki bir aynaya gönderilen bir ışık huzmesinden oluşur. Kaynaktan aynaya giderken huzme dönen dişli bir çarktan geçer. Belli bir dönme hızında huzme giderken bir boşluktan ve dönerken başka bir boşluktan geçer ancak biraz düşük ya da yüksek dönme hızlarında huzme dişlerden birine çarpar ve çarktan geçemez. Dişliyle ayna arasındaki mesafeyi, çarktaki diş sayısını ve dönme hızını bilerek ışığın hızı hesaplanabilir.[15]
Bu günlerde bir nanosaniyeden (ns) az zaman çözünürlüğü olan salınım izlerler sayesinde ışığın hızı bir lazer ya da LED' den gelen ışık nabzının aynadan yansımasının zamanı ile direkt olarak ölçülebilir. Bu metot diğer modern teknikler kadar isabetli değildir anca bazı üniversite fizik sınıflarında laboratuvar deneyi olarak kullanılır..[32][33][34]
Elektromanyetik sabitler
C'yi elektromanyetik dalgaların yayılımına bağlı olmadan hesaplamanın bir yolu Maxwell' in teorisinde kullanılan c, ε0 ve μ0 arasındaki ilişkiyi kullanmaktır. ε0 kapasitans ve kapasitörün boyutları hesaplanarak bulunabilir. μ0 ise 4π×10−7 H·m−1 olarak sabittir. 1907'de Rosa ve Dorsey bu metodu kullanarak 299710±22 km/s değerini bulmuşlardır.[35][36]
Boşluk rezonansı

Işık hızını ölçmenin başka bir yolu da elektromanyetik bir dalganın boşluktaki frekansını ve dalga boyunu ayrı ayrı ölçmektir. c' nin değeri c=fλ eşitliği ile bulunabilir. Bir seçenek de boşluk rezonansının rezonans frekansını ölçmektir. Eğer rezonans boşluğunun boyutları biliniyorsa dalganın dalga boyunu bulmak için kullanılabilir. 1946'da Louis Essen ve A.C Gordon-Smith, boyutları bilinen bir mikrodalga boşluğunun mikro dalgalarının normal modlarının farklılıkları için bir frekans bulmuşlardır. Modların dalga boyları boşluğun geometirisi ve elektromanyetik teorisinden bilindiği için ilgili frekansların bilinmesi ışık hızının hesaplanmasına yardımcı olmuştur.[35][37]
Essen–Gordon-Smith sonucu,299792±9 km/s, optik tekniklerle bulunanlardan çok daha isabetliydi. 1950 yılına kadar Essen tarafından yapılan tekrarlı ölçümler 299792.5±3.0 km/s sonucunu vermiştir.[38]
Bu teknik evde mikrodalga fırın ve marşmelov ya da margarin gibi yemek yardımıyla da gözlemlenebilir: eğer döner masa kaldırılırsa yemek hareket etmez, en hızlı olarak antidotlarda pişer ve erimeye başlar. Böyle iki nokta arasındaki mesafe mikrodalganın dalga boyunun yarısıdır; bu mesafeyi ölçüp dalga boyunu mikrodalga frekansıyla çarparak c genelde 5% den daha az bir hatayla hesaplanabilir.[39][40]
İnterferometre

İnterferometre elektromanyetik radyasyonun dalga boyunu bularak ışık hızını hesaplamanın başka bir yoludur. Frekansı bilinen uyumlu bir ışık huzmesi iki yolu izlemesi için bölünür ve tekrar birleşir. Etki düzlemini gözlemlerken yolun uzunluğunu ayarlayarak ve yol uzunluğundaki değişimi dikkatlice ölçerek ışığın dalga boyu bulunabilir. Sonra ışık hızı c = λf denklemi ile hesaplanır.
Lazer teknolojisinin gelişmesinden önce uyumlu radyo kaynakları ışık hızının interferometrik ölçümleri için kullanılırdı. Ancak; dalga boylarının interferometrik hesaplanması dalga boyları ile birlikte daha isabetsiz hale gelmeye başladı ve bu yüzden deneyler radyo dalgalarının uzun dalga boyları(~0.4 cm) ile sınırlandı. Netlik kısa dalga boyları ile artırılabilir ama o zaman da ışığın frekansını direkt olarak ölçmek zorlaşır. Bu sorunu çözmenin bir yolu, frekansı hesaplanabilen düşük frekanslı br sinyalle başlayıp bu sinyalden giderek daha yüksek frekanslı sinyaller sentezlemektir. Daha sonra bir lazer frekansa sabitlenip dalga boyu interferometre kullanılarak bulunabilir. 3,5×10-9.[41][42]
Tarih
| <1638 | Galileo, covered lanterns | inconclusive[Note 8] |
| <1667 | Accademia del Cimento, covered lanterns | inconclusive[Note 9] |
| 1675 | Rømer and Huygens, moons of Jupiter | 220000[43][44] |
| 1729 | James Bradley, aberration of light | 301000[15] |
| 1849 | Hippolyte Fizeau, toothed wheel | 315000[15] |
| 1862 | Léon Foucault, rotating mirror | 298000±500[15] |
| 1907 | Rosa and Dorsey, EM constants | 299710±30[35][36] |
| 1926 | Albert A. Michelson, rotating mirror | 299796±4[45] |
| 1950 | Essen and Gordon-Smith, cavity resonator | 299792,5±3,0[38] |
| 1958 | K.D. Froome, radio interferometry | 299792,50±0,10[46] |
| 1972 | Evenson et al., laser interferometry | 299792,4562±0,0011[42] |
| 1983 | 17th CGPM, definition of the metre | 299792,458 (exact)[47] |
Modern periyotun erken bölümlerine kadar ışığın anlık mı yoksa son derece hızlı ölçülebilir bir hızla mı hareket ettiği bilinmiyordu. Bu olayın ilk ölçüldüğü olay antik Yunanistan' daydı. Antik Yunanlar, Müslüman ve Avrupalı bilimciler Romer ışık hızının ilk hesaplarını sağlayana kadar bunu tartıştılar. Einstein'ın İzafiyet Teorisi ışık hızının referans çerçevesi ne olursa olsun sabit olduğunu göstermiştir. O zamandan bu yana bilim adamları giderek daha isabetli hale gelen ölçümler yapmışlardır.
Erken Tarih
Empedocles ışığın ölçülebilir hızı olduğunu iddia eden ilk kişiydi. Işığın hareket eden bir şey olduğunu dolayısıyla hareketinin zaman alması gerektiğini öne sürdü. Aristo ise tam tersini öne sürüp "ışığın bir şeyin varlığından oluştuğunu ve hareket etmediğini öne sürmüştür. Euclid ve Ptolemy Empedocles'in ışığın gözlerden emilerek görüşü sağladığı yolundaki teorisini ilerletmişlerdir. Bu teoriye dayanarak Alexandrialı Heron yıldızlar gibi uzak nesneler gözümüzü açtığımız anda görülebildiği için ışığın hızının sonsuz olduğunu ileri sürmüştür. Hindu Vedas'ta bahsedildiği üzere Sayana ışık hızının hesaplanması üzerine yorumlar yapmıştır. Eski İslam filozofları ilk başta Aristo'nun görüşlerine katılmışlardır. 1021'de Alhazen Optik Kitabını yayınlayarak görüş teorisine karşı çıkmış ve ışığın nesnelerden göze geldiğini öne süren ve şimdi kabul edilmiş olan intromisyon teorisini savunmuştur. Bu da Alhazen'i ışığın ölçülebilir hızı olduğunu öne sürmeye yönlendirmiştir. Işığın bir madde olduğunu, yayılmasının bizim hislerimiz tarafından fark edilmese de zaman aldığını söylemiştir. Ayrıca 11. yüzyılda Abu Rayhan al Biruni de ışığın ölçülebilir hızı olduğunu söylemiş ve ışığın sesten çok daha hızlı olduğunu gözlemlemiştir.[48]
13. yüzyılda Roger Bacon filozofik argümanları Alhazen ve Aristo'nun da yazdıklarıyla destekleyerek ışığın havadaki hızının sonsuz oladığını öne sürmüştür. 1270' lerde Witelo ışığın boşlukta sonsuz hızla hareket edip daha yoğun ortamlarda yavaşladığını düşünmüştür.[49]
17. yüzyıl başlarında Johannes Kepler boş uzay herhangi bir engel sunmadığı için ışık hızının sonsuz olduğuna inanmıştır. Rene Descartes eğer ışığın hızı ölçülebilir olsaydır Güneş, Dünya ve Ay'ın bir ay tutulması sırasında düzen dışında olacağını öne sürdü. Böyle bir düzensizlik de gözlemlenmediği için Descartes ışık hızının sonsuz olduğunu varsaydı. Descartes eğer ışığın hızının ölçülebilir olduğu keşfedilirse kendisinin bütün filozofi sisteminin yerle bir olacağını söyledi. Snell Yasası'nın Descartes derivasyonunda ışık hızı anlık olmasına rağmen çevre ne kadar yoğunsa ışık o kadar yavaştır. Fermat da ölçülebilir ışık hızını savunmuştur.[50]
İlk ölçüm girişimleri
1629'da Isaac Beeckman bir kişinin ışık patlamasının bir mil uzaklıktaki bir aynadan yansımasını gözlemlediği bir deney önermiştir. 1638'de Galileo Galilei bir feneri açıp bir mesafedeki algısını gözlemleyeceği ve aradaki gecikmeden ışık hızını ölçebileceği bir deney ortaya atmıştır. Işığın anlık hareket edip etmediğini ayırt edememiştir ancak etmiyorsa dahi inanılmaz hızlı olduğu sonucuna varmıştır. 1667'de Accademia del Cimento Galileo'nun deneyini 1 mil uzaklıktaki bir fenerle uyguladığını ve gecikme gözlemlemediğini söylemiştir. Bu deneydeki gerçek gecikme 11 mikrosaniye civarında olurdu.

Işık hızının ilk miktarsal tahmini 1676'da Romer tarafından yapılmıştır. Dünya, Jüpiter'e yaklaşırken Jüpiter'in uydusu Io'nun uzaklaşırken gözüktüğünden daha kısa olduğunu gözlemiş ve ışığın ölçülebilir hızının olduğu sonucuna varmıştır ve Dünya' nın yörüngesinin çapını 22 dakikada geçtiğini tahmin etmiştir. Christian Huygens bu tahmini Dünya'nın yörüngesinin çapının bir tahiniyle birleştirmiş ve ışığın hızını yaklaşık 220000 km/sn olarak bulmuştur.[44]
1704' te yayınladığı kitabı Optics'de Newton Romer'in hesaplarını yazmış ve ışığın Güneş'ten Dünya'ya ulaşma süresini 7 ya da 8 dakika olarak belirtmiştir. Newton Romer'in tutulma gölgelerinin renkli olup olamadığını soruşturmuş ve olmadığını duyunca farklı renklerin aynı hızda hareket ettikleri sonucuna varmıştır. 1729'da James Bradlet yıldızsal sapmayı keşfetti. Buradan yola çıkarak ışığın Dünya'nın yörüngesindeki hareketinden 10210 kere daha hızlı hareket ettiği sonucuna vardı.[29]
Elektromanyetizm ile bağlantılar
19. yüzyılda Hippolyte Fizeau Dünya'daki uçuş zamanlarına dayanarak ışık hızını hesaplamak için bir metot geliştirdi ve 315000 km/sn lik bir değer buldu. Metodu Leon Foucault'un 1862'de 298000 km/s' lik değer bulan metodundan geliştirilmişti.1856'da Wilhelm Eduard Weber ve Rudolf Kohlrausch eletromanyetik ve eletrostatik şarj birimlerini bir Leyden kavanozunun şarjını boşaltarak ölçüp numarasal değerinin ışık hızına çok yakın olduğunu bulmuşlardır. Bir sonraki yıl Gustav Kirchoff dirençsiz bir telde elektrik sinaylinin de bu hızda ilerlediğini bulmuştur. Erken 1860' larda Maxwell üzerinde çalıştığı eletromanyetizma teorisine göre elektromanyetik dalgaların boş uzyda Weber/ Kohraush oranında bulunan hızda hareket ettiğini bulmuştur.[51]
"Luminiferous aether"

Zamanında boş uzayın arka planda Luminiferous aether adlı içinde elektromanyetik alan bulunduran bir nesneyle dolu oluduğu düşünülüyordu. Bazı fizikçiler aether'ı ışığın yayılmasının tercih edilen referans çerçevesi olduğunu düşünmüştür ve dünyanın hareketini bu çevrede ölçülebileceğine inanmıştır. 1880' lerden itibaren bunu tespit etmek için çeşitli deneyler yapılmıştır. Bunların en meşhuru A. A. Michelson ve E. W. Morley tarafından 1887' de yapılmıştır. Tespit edilen hareket her zaman gözlemsel hatadan daha azdı. Modern deneyler ışığın çift yönlü hızının saniyede 6 nanometreye kadar izotopik olduğunu işaret etmektedir. Bu deney nedeniyle Lorentz teçhizatın aether içindeki hareketinin teçhizatın hareketin yönündeki uzunluğunu daraltabileceğini öne sürmüş ve hareket halindeki sistemler için zaman değişkeninin de buna göre değişebileceğini varsaymıştır ve bu da Lorentz değişimi formülüne yol açmıştır. Lorentz' in aether teorisinden yola çıkara Henri Poincare(1900) yerel zamanın aether içinde hareket eden saatler tarafından gösterildiğini göstermiştir. 1904' te Lorentz' in teorilerinin doğrulanması halinde ışık hızının dinamikte sınırlayıcı bir faktör olabileceğini öne sürmüştür. 1905' te Lorentz' in aether teorisini görelilik prensibiyle gözlemsel anlaşmaya getirmiştir.[52][53]
Özel Görelilik
1905'te Einstein ışığın boşlukta hızlanmayan bir gözlemci tarafından ölçülen hızının kaynaktan ya da gözlemciden bağımsız olduğunu öne sürmüştür. Bunu ve görelilik prensibini kullanarak Özel Görelilik Kuramı' nı ortaya atmıştır. Bu da hareketsiz aether konseptini kullanışsız hale getirmiştir ve uzay ve zaman konseptlerinde devrim yaratmıştır.[54][55]
C'nin artan doğruluğu ve metre ile saniyenin yeniden tanımlanması
20. yüzyılın ikinci yarısında ışık hızının ölçümünün daha isabetli olması konusunda, ilk önce boşluk rezonansı tekniği ile daha sonra da lazer interferometer teknikleriyle birçok gelişme katedildi bunlara metre ve saniyenin yeni ve daha kesin tanımları da yardımcı oldu. 1950'de Louis Essen hızı boşluk rezonansını kullanarak 299792.5±1 km/s olarak hesapladı. Bu değer 12. Radyo-Bilimsel Genel buluşması tarafından kabul edildi. 1960'ta metre krypton-86 spectral düzleminin belli bir dalga boyuna göre yeniden tanımlandı ve 1967'de saniye caesium-133'ün ince geçiş frekansına göre yeniden tanımlandı.
1972' de lazer interferometre metodu ve yeni tanımlar kullanılarak NBS Boulder, Colorado'da bir grup ışığın boşluktaki hızını 299.792.456,2 ± 1,1 m/s olarak hesapladı. Bu daha önce kabul edilen değerden 100 kat daha belirgin bir değerdi. Geri kalan belirsizlik çoğunlukla metrenin tanımına bağlıdır.[56]
Işık hızını belirgin bir sabit olarak tanımlamak
1983'te 17. CGPM frkans ölçümlerindeki dalga boylarının ve ışık hızı için geçerli değerin bir önceki standarttan daha tekrarlanabilir olduğunu bulmuştur. Saniyenin 1967'deki tanımı sabit bıraktılar, bu nedenle caesium ince frekansı şu an hem metreyi hem de saniyeyi tanımlamaktadır. Bunu yapabilmek için metreyi "ışığın boşlukta saniyenin 1/299792458'inde aldığı mesafe"olarak tanımladılar. Bu tanımın bir sonucu olarak ışığın boşluktaki hızı tam olarak 299792458 m/s'dir ve SI tarafından tanımlanan bir sabit haline gelmiştir. ".[57][58]
2011'de CGPM bütün temel SI birimlerini "belirgin-sabit formülasyonunu" kullanarak yeniden tanımlamak niyetinde olduğunu belirtmiştir. Bu metrenin yeni ama tamamen denk bir tanımını sunmuştur: "metre, uzunluk birimi, ışığın boşluktaki hızının SI birimi s−1 ile yazılımında 299792458 olan büyüklüktür.
Notlar
Kaynakça
- ^ Larson, Ron; Hostetler, Robert P. (2007). Elementary and Intermediate Algebra: A Combined Course, Student Support Edition (4. resimli bas.). Cengage Learning. s. 197. ISBN 978-0-618-75354-3. 19 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Kasım 2020.
- ^ Uzan, J-P; Leclercq, B (2008).
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) 5 Kasım 2013 tarihinde Wayback Machine sitesinde arşivlendi. (PDF) (8th ed.), p. 112, ISBN 92-822-2213-6
- ^ Gibbs, P (2004) [1997].
- ^ Mendelson, KS (2006).
- ^ See for example:
- ^ Gibbs, P (1997) [1996].
- ^ Uzan, J-P (2003).
- ^ Amelino-Camelia, G (2008).
- ^ Herrmann, S; et al. (2009).
- ^ Lang, KR (1999).
- ^ Fowler, M (March 2008).
- ^ Tolman, RC (2009) [1917].
- ^ Quimby, RS (2006).
- ^ a b c d e f g Gibbs, P (1997).
- ^ Sakurai, JJ (1994).
- ^ Wynne, K (2002).
- ^ Chase, IP.
- ^ Harrison, ER (2003).
- ^ Panofsky, WKH; Phillips, M (1962).
- ^ Amelino-Camelia, G (2009).
- ^ Cromie, William J. (24 Ocak 2001). "Researchers now able to stop, restart light". Harvard University Gazette. 28 Ekim 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Kasım 2011.
- ^ a b Milonni, PW (2004). "2".
- ^ Cherenkov, Pavel A. (1934).
- ^ Parhami, B (1999).
- ^ "Theoretical vs real-world speed limit of Ping" 2 Eylül 2010 tarihinde Wayback Machine sitesinde arşivlendi..
- ^ Further discussion can be found at "StarChild Question of the Month for March 2000" 29 Ocak 2014 tarihinde Wayback Machine sitesinde arşivlendi..
- ^ "Time is money when it comes to microwaves" 27 Mayıs 2015 tarihinde Wayback Machine sitesinde arşivlendi..
- ^ a b Bradley, J (1729).
- ^ Pitjeva, EV; Standish, EM (2009).
- ^ IAU Working Group on Numerical Standards for Fundamental Astronomy.
- ^ Cooke, J; Martin, M; McCartney, H; Wilf, B (1968).
- ^ Aoki, K; Mitsui, T (2008).
- ^ James, MB; Ormond, RB; Stasch, AJ (1999).
- ^ a b c Essen, L; Gordon-Smith, AC (1948).
- ^ a b Rosa, EB; Dorsey, NE (1907).
- ^ Essen, L (1947).
- ^ a b Essen, L (1950).
- ^ Stauffer, RH (April 1997).
- ^ "BBC Look East at the speed of light" 23 Ağustos 2007 tarihinde Wayback Machine sitesinde arşivlendi..
- ^ Sullivan, DB (2001).
- ^ a b Evenson, KM; et al. (1972).
- ^ "Touchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences" 21 Temmuz 2011 tarihinde Wayback Machine sitesinde arşivlendi. (PDF).
- ^ a b Huygens, C (1690).
- ^ Michelson, A. A. (1927).
- ^ Froome, KD (1958).
- ^ "Resolution 1 of the 17th CGPM" 26 Haziran 2013 tarihinde Wayback Machine sitesinde arşivlendi..
- ^ O'Connor, JJ; Robertson, EF.
- ^ Marshall, P (1981).
- ^ Carl Benjamin Boyer, The Rainbow: From Myth to Mathematics (1959)
- ^ O'Connor, JJ; Robertson, EF (November 1997).
- ^ Darrigol, O (2000).
- ^ Galison, P (2003).
- ^ Miller, AI (1981).
- ^ Pais, A (1982).
- ^ "Resolution 2 of the 15th CGPM" 7 Ekim 2008 tarihinde Wayback Machine sitesinde arşivlendi..
- ^ Adams, S (1997).
- ^ Rindler, W (2006).