Teknik resim, bir şeyin nasıl çalıştığını veya üretildiğini anlamak üzere yapılan çizim. Mühendisler arasındaki iletişimi en kolay ve en doğru şekilde sağlaması açısından büyük öneme sahip teknik bir alfabedir. Temelde doğrular ve eğrilerin çeşitli şekillerde bir araya gelmesiyle oluşan teknik resim, yapılması istenen konstrüksiyon ve tasarımın kâğıt üzerinde tanımlanması sanatıdır.
Olasılık kuramı ve istatistik bilim dallarında t-dağılımı ya da Student'in t dağılımı genel olarak örneklem sayısı veya sayıları küçük ise ve anakütle normal dağılım gösterdiği varsayılırsa çıkartımsal istatistik uygulaması için çok kullanılan bir sürekli olasılık dağılımıdır. Çok popüler olarak tek bir anakütle ortalaması için güven aralığı veya hipotez sınaması ve iki anakütle ortalamasının arasındaki fark için güven aralığı veya hipotez sınamasında, yani çıkarımsal istatistik analizlerde, uygulama görmektedir.
Normal dağılım, aynı zamanda Gauss dağılımı veya Gauss tipi dağılım olarak isimlendirilen, birçok alanda pratik uygulaması olan, çok önemli bir sürekli olasılık dağılım ailesidir.
Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir nesnedir. a ve b sayıları gerçek olursa karmaşık sayılar şu biçimde gösterilirler:
Ortalama veya merkezsel konum ölçüleri, istatistik bilim dalında ve veri analizinde kullanılan bir veri dizisinin orta konumunu, tek bir sayı ile ifade eden betimsel istatistik ölçüsüdür. Günlük hayatta ortalama dendiğinde genellikle kast edilen aritmetik ortalama olmakla beraber bu ölçünün çok belirli bazı dezavantajları söz konusudur. Bu yüzden matematik ve istatistikte, bir anakütle veya örneklem veri dizisi değerlerini temsil eden tek bir orta değer veya beklenen değer, olarak medyan (ortanca), mod (tepedeğer), geometrik ortalama, harmonik ortalama vb adlari verilen birçok değişik merkezsel konum ölçüleri geliştirilmiş ve pratikte kullanılmaktadır.
Standart sapma, Olasılık kuramı ve istatistik bilim dallarında, bir anakütle, bir örneklem, bir olasılık dağılımı veya bir rassal değişken, veri değerlerinin yayılımının özetlenmesi için kullanılan bir ölçüdür. Matematik notasyonunda genel olarak, bir anakütle veya bir rassal değişken veya bir olasılık dağılımı için standart sapma σ ile ifade edilir; örneklem verileri için standart sapma için ise s veya s'
Harmonik ortalama, gözlem sonuçlarının terslerinin aritmetik ortalamasının tersidir.
Merkezi limit teoremi büyük bir sayıda olan bağımsız ve aynı dağılım gösteren rassal değişkenlerin aritmetik ortalamasının, yaklaşık olarak normal dağılım göstereceğini ifade eden bir teoremdir. Matematiksel bir ifadeyle, bir merkezi limit teoremi olasılık kuramı içinde bulunan bir zayıf yakınsama sonucu setidir. Bunların hepsi, birçok bağımsız aynı dağılım gösteren rassal değişkenlerin herhangi bir toplam değerinin limitte belirli bir "çekim gücü gösteren dağılıma" göre dağılım gösterme eğiliminde olduğu gerçeğini önerir.
Çarpıklık olasılık kuramı ve istatistik bilim dallarında bir reel-değerli rassal değişkenin olasılık dağılımının simetrik olamayışının ölçülmesidir.
Bir genelleştirilmiş ortalama; Pisagorik ortalamalarını, yani aritmetik ortalama, geometrik ortalama ve harmonik ortalamayı, aynı tanım formülünde birleştirip kapsayan bir soyut genelleştirmedir. Güç ortalaması veya Holder ortalaması adları da verilmektedir.
Olasılık kuramı ve istatistik bilim dallarında log-normal dağılım logaritması normal dağılım gösteren herhangi bir rassal değişken için tek-kuyruklu bir olasılık dağılımdır. Eğer Y normal dağılım gösteren bir rassal değişken ise, bu halde X= exp(Y) için olasılık dağılımı bir log-normal dağılımdır; aynı şekilde eğer X log-normal dağılım gösterirse o halde log(X) normal dağılım gösterir. Logaritma fonksiyonu için bazın ne olduğu önemli değildir: Herhangi iki pozitif sayı olan a, b ≠ 1 için eğer loga(X) normal dağılım gösterirse, logb(X) fonksiyonu da normaldir.
İstatistik bilim dalında ağırlıklı ortalama betimsel istatistik alanında, genellikle örneklem, veri dizisini özetlemek için bir merkezsel konum ölçüsüdür. En çok kullanan ağırlıklı ortalama tipi ağırlıklı aritmetik ortalamadır. Burada genel olarak bir örnekle bu kavram açıklanmaktadır. Değişik özel tipli ağırlıklar alan özel ağırlıklı aritmetik ortalamalar bulunmaktadır. Diğer ağırlıklı ortalamalar ağırlıklı geometrik ortalama ve ağırlıklı harmonik ortalamadir. Ağırlıklı ortalama kavramı ile ilişkili teorik açıklamalar son kısımda ele alınacakdır.
Matematikte ıraksak seri yakınsak olmayan bir sonsuz seridir. Bu, serinin kısmi toplamlarının herhangi bir limit değeri olmadığı anlamına gelmektedir.
Alman Standartlar Enstitüsü, Federal Almanya Cumhuriyeti'nin resmî standart enstitüsü olup merkezi başkent Berlin'dedir.
Karekök 2 ya da kök 2, kendisi ile çarpıldığında 2'yi veren pozitif cebirsel sayıdır. 2'nin kökü mühendislikte genellikle 1.414 olarak alınsa da, gerçek değeri tam olarak bu değildir.Gösterimi
şeklindedir.
Dönel simetrisi olan bir cisim, belli bir dönmeden sonra aynı görünür. Bir cismin birden çok dönel simetriği olabilir; örneğin, yansıma ve ters çevrilmeyi saymazsak, Man Adası bayrağında görünen triskelion şeklinin üç adet dönel simetriği vardır, bir diğer deyişle üçlü simetriye sahiptir. Dönel simetri derecesi, bir şeklin başka bir kenarından veya köşesinden aynı görünmesi için kaç derece döndürülmesi gerektiği anlamına karşılık gelir.
Termodinamik ve katı hal fiziğinde Debye modeli; Peter Debye tarafından 1912 yılında geliştirilen, katılarda özgül ısıya (ısı kapasitesi) olan fonon katkısını tahmin etmek için kullanılan metottur. Atomik kristal yapının salınımlarını, bir kutu içerisindeki fononlar gibi düşünerek ele alır. Bu; katıya ayrı ayrı kuantum harmonik osilatörlerden oluşmuş olarak davranan Einstein modelinin tam tersidir. Debye modeli; 
– Debye T3 yasası - ısı kapasitesini düşük sıcaklıklarda doğru bir şekilde tahmin eder., düşük sıcaklıklarda olan. Tıpkı Einstein modeli gibi, yüksek sıcaklıklarda Dulong–Petit Yasasını da doğru bir şekilde kapsar. Ama, ara sıcaklıklarda basitleştirmek için yapılan varsayımlar nedeniyle doğruluğu kusurludur.
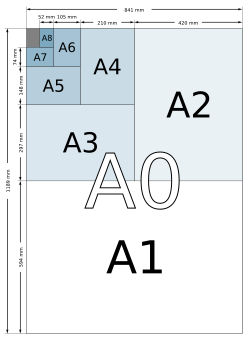
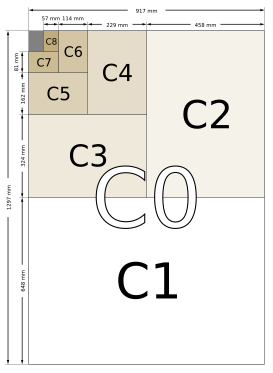
Kâğıt boyutları, dünya genelinde standart olarak kullanılan boyutları kapsar. Kâğıt farklı boyutlarda gelir. Farklı kâğıt boyutları için adlar vardır. Dünyanın farklı bölgelerinde farklı boyut ve isimler kullanılır.
Tane boyutu münferit tortu tanelerinin çapı veya kırıntılı kayaçlardaki lithified parçacıklardır. Terim ayrıca diğer zerre şekilli malzemelere de uygulanabilecektir. Bu, bir parçacık veya tahıl içindeki tek bir kristalin boyutunu ifade eden kristalit boyutundan farklıdır. Tek bir tane birkaç kristalden oluşabilir. Granül malzeme çok küçük kolloidal parçacıklardan kil, silt, kum, çakıl ve parke taşlarından kayalara kadar değişebilir.
Temel cebirde, kuadratik formül, bir ikinci dereceden denklemin köklerini (çözümlerini) bulan bir formüldür. İkinci dereceden bir denklemi çözmek için ikinci dereceden formülü kullanmak yerine çarpanlara ayırma, tam kareye tamamlama, grafik çizme ve diğerleri gibi başka yollar da vardır.
