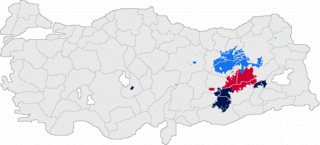
Zazaca, Hint-Avrupa dil ailesinin İran dilleri grubunda bulunan Kuzeybatı İran koluna bağlı bir dildir. Zazalar tarafından Türkiye'nin doğusunda Bingöl, Elâzığ, Erzincan, Erzurum, Sivas ve Tunceli; güneydoğusunda Diyarbakır, Adıyaman, Şanlıurfa ile Muş'un Varto ilçesi ve Bitlis'in batısında Mutki ilçesi civarındaki köylerde yoğunlukla konuşulur. Zazacaya gramer, genetik, dil bilimi ve söz varlığı açısından en yakın diller Hazar Denizi kıyılarında konuşulan Talışça, Tatça, Gilekçe, Simnanca, Sengserce ve Mazenderancadır.

Bilim veya ilim, nedensellik, merak ve amaç besleyen, olguları ve iddiaları deney, gözlem ve düşünce aracılığıyla sistematik bir şekilde inceleyen entelektüel ve uygulamalı disiplinler bütünüdür. Kimi kullanımlarda bu tanımın "ilim" için geçerli olmadığının altını çizmek gerekir. Çünkü bilim somut, evrensel olayları kendine konu edinmişken ilim doğaötesi olaylarla da ilgilenebilir fakat somut kanıt sunmaz. Bilimi sınıflandıran bilim felsefecileri bilimi formal bilimler, sosyal bilimler ve doğa bilimleri olmak üzere üçe ayırır. Bilimin diğer tüm dallardan en ayırt edici özelliği, savunmalarını somut kanıtlarla sunmasıdır. Bu sayede bilim, bilinmeyen olguları açıklamamıza ve evreni idrak etmemize güçlü destek olur.

Ernst Ingmar Bergman, İsveçli oyun yazarı ve film yönetmeni.

Doğu Roma İmparatorluğu veya Bizans İmparatorluğu ya da kısaca Bizans, Geç Antik Çağ ve Orta Çağ boyunca Roma İmparatorluğu'nun devamı şeklinde var olan ve başkenti Konstantinopolis olan ülke. 5. yüzyılda Batı Roma İmparatorluğu'nun dağılışı ve çöküşü sürecinden sonra ayakta kalan imparatorluk, 1453'te Osmanlı'ya yenik düşünceye kadar yaklaşık bin yıl boyunca var olmaya devam etmiştir. Var olduğu sürenin başı ve ortalarını kapsayan çoğunda, Avrupa'da ekonomik, kültürel ve askerî bakımdan en güçlü ülkeydi. "Bizans İmparatorluğu" ve "Doğu Roma İmparatorluğu" terimleri ülkenin yıkılışından sonraki tarihçiler tarafından yaratılmış olup imparatorluk vatandaşları kendi ülkelerine Roma İmparatorluğu, veya Romania ; kendilerineyse "Romalılar" demekteydi.

Astronomide zodyak, ekliptiğin her iki yanında 9° uzanan, Ay'ın ve ana gezegenlerin yörüngelerini kapsayan bir kuşağı ifade eder. Ekliptik üzerinde merkezlenen gökyüzü koordinat merkezinin bir özelliğidir, ekinoks noktasının doğusunda derece cinsinden ölçülen gök boylamının ölçülen değeridir.

Pergeli Apollonius, konik kesitler üzerindeki çalışmaları ile tanınan Antik Yunan geometri uzmanı ve astronom. Öklid ve Arşimet'in konuya katkılarından başlayarak, onları analitik geometrinin icadından önceki duruma getirdi. Elips, parabol ve hiperbol terimlerinin tanımları bugün kullanımda olanlardır.

Daniel Bernoulli İsviçreli matematikçi ve fizikçidir. Bernoulli ailesindeki ünlü matematikçilerdendir. Özellikle matematiği akışkan mekaniği alanına uyarlamasıyla bilinir. Olasılık ve istatistik alanındaki çalışmalarıyla bu alanların gelişimine öncülük etmiştir. İsmi, 20. yüzyılın iki önemli teknolojisinin çalışmasının altında yatan matematiği tanımlayan Bernoulli İlkesi ile bütünleşmiştir. Bahsi geçen bu iki önemli teknoloji karbüratör ve uçak kanadıdır.

Johann Carl Friedrich Gauss ya da Gauß, Alman matematikçi, astronom, istatistikçi, olağanüstü katkılardan dolayı "Matematikçilerin prensi" ve "antik çağlardan beri yaşamış en büyük matematikçi" olarak anılır.
Aynî hak, kişilerin eşya üzerinde doğrudan doğruya hakimiyetini sağlayan ve bu nedenle herkese karşı ileri sürülebilen haklardandır. Özellikle de eşya hukukunda, hak sahibinin, söz konusu eşya üzerindeki tasarruf yetkisini tespit etme bakımından, hakkın sınırının tespit edilmesi büyük önem taşımaktadır. Bu hakkın aynî hak olması hâlinde farklı, olmaması hâlinde farklı hükümler uygulanabilecektir.

Üçgenlerle ilgili erken çalışmalar, Mısır matematiği ve Babil matematiğinde MÖ 2. binyıla kadar izlenebilir. Trigonometri, Kushite matematiğinde de yaygındı. Trigonometrik fonksiyonların sistematik çalışması Helenistik matematikte başladı ve Helenistik astronominin bir parçası olarak Hindistan'a ulaştı. Hint astronomisinde trigonometrik fonksiyonların incelenmesi, özellikle sinüs fonksiyonunu keşfeden Aryabhata nedeniyle Gupta döneminde gelişti. Orta Çağ boyunca, trigonometri çalışmaları İslam matematiğinde El-Hârizmî ve Ebu'l-Vefâ el-Bûzcânî gibi matematikçiler tarafından sürdürüldü. Altı trigonometrik fonksiyonun da bilindiği İslam dünyasında trigonometri bağımsız bir disiplin haline geldi. Arapça ve Yunanca metinlerin tercümeleri trigonometrinin Latin Batı'da Regiomontanus ile birlikte Rönesans'tan itibaren bir konu olarak benimsenmesine yol açtı. Modern trigonometrinin gelişimi, 17. yüzyıl matematiği ile başlayan ve Leonhard Euler (1748) ile modern biçimine ulaşan Batı Aydınlanma Çağı boyunca değişti.
Sonsuz küçükler, ölçülemeyecek kadar küçük cisimleri tarif etmek için kullanılır. Sonsuz küçüklerden yararlanmaktaki asıl amaç nicelik bakımından çok küçük olsalar da hala açı, eğim gibi belirli özelliklere sahip olmalarıdır. Sonsuz küçük kelimesi 17. Yüzyıl Modern Latin uydurma sözcüğü olan bir dizideki “sonsuzuncu” terim anlamına gelen infitesimustan gelmektedir. İlk olarak 1670 yılı civarında Nicolas Marecator ya da Gottfried Wilhelm Leibniz tarafından kullanılmıştır. Genel anlamla sonsuz küçük bir cisim herhangi bir uygulanabilir ölçümden küçük olan ama boyut olarak sıfırdan farklı ya da çok küçük olan ve bu nedenle sıfırdan ayırt edilemeyecek durumdaki cisimdir. Bundan dolayı sonsuz küçük ifadesi sıfat olarak kullanıldığında aşırı derecede küçük anlamına gelmektedir. Bir anlam verebilmek için genellikle aynı bağlamdaki başka bir sonsuz küçük ile karşılaştırılması gerekir. Sonsuz miktarda çok sonsuz küçük bir integral üretmek amacıyla toplanır. Arşimet “Mekanik Teoremlerin Metodu” adı verilen çalışmasında katı cisimlerin hacimlerini ve bölgelerin alanlarını bulmak için Bölünmezler Yöntemi olarak bilinen yöntemi kullanmıştır. Yayımlanan resmi bilimsel eserlerinde aynı problemleri Tüketme Yöntemi ile çözmüştür. 15. Yüzyılda Cusalı Nicholas’ın üzerinde çalıştığı bir çemberin alanını çemberi sonsuz kenarlı bir çokgen olarak hesaplama yöntemi 17. Yüzyılda Johannes Kepler tarafından geliştirilmiştir. Simon Stevin’in 16. Yüzyılda tüm sayıların ondalık gösterimi üzerine yaptığı çalışmalar gerçek sürekliliğe temel hazırladı. Bonaventura Cavalieri’nin bölünmezler yöntemi klasik yazarların sonuçlarını genişletmesine olanak sağladı. Bölünmezler yöntemi, eş boyutlu varlıklardan oluşan geometrik figürler ile ilişkilidir. John Wallis’in sonsuz küçük görüşü geometrik figürleri figürle aynı boyuta sahip sonsuz yapı bloğuna bölmesi ile bölünmezler yönteminden ayrılır. Bu görüş integral kalkülüsünün genel yöntemleri için temel hazırlamıştır. Sonsuz küçükleri alan hesabında  ile göstermiştir. Leibniz tarafından kullanılan sonsuz küçükler, sonlu ve sonsuz sayılar için başarılı olan Süreklilik Kuramı ve belirlenemez miktarlar için gösterimi değiştirmenin yönteminin sadece belirlenebilir olanları göstererek yapılacağını anlatan Aşkın Homojenite Yasası gibi bulgusal prensiplere dayanmaktaydı. 18. Yüzyıl sonsuz küçüklerin Leonard Euler ve Joseph-Louis Lagrange gibi matematikçiler tarafından sıklıkla kullanıldığı bir zaman aralığı olmuştur. Augustin-Louis Cauchy sonsuz küçükleri Cour d’Analyse adlı eserinde sürekliliği açıklamak için ve Dirac delta fonksiyonunun ilk formlarından birini tanımlarken kullanmıştır. Tıpkı Cantor ve Dedekind’ın Stevin’in sürekliliğinin daha soyut bir halini geliştirdikleri gibi Paul du Bois-Reymond da sonsuz küçük ile zenginleştirilmiş süreklilik üzerine fonksiyonların artış oranını temel alan bir seri çalışma yapmıştır. Du Bois-Reymond’un çalışması Emile Boral ve Thoralf Skolem’ e ilham verdi. Borel Bois-Reymond’un çalışmalarını Cauchy’nin sonsuz küçüklerin artış oranına dair çalışmalarıyla bağlantı kurdu. Skolem 1934’te aritmetiğin standart dışı ilk modellerini geliştirdi. Süreklilik ve sonsuz küçük yasalarının matematiksel “implementasyonu” Abraham Robinson tarafından 1961’de yapılmıştır. Robinson ayrıca Edwin Hewirr’in 1948’de ve Jerzy Łoś’un 1955’teki çalışmalarına dayanarak standart dışı analizi geliştirmiştir. Hipergerçekler sonsuz küçük ile zenginleştirilmiş sürekliliği sağlar ve transfer prensibi de Leibniz’in süreklilik yasasını sağlar.
ile göstermiştir. Leibniz tarafından kullanılan sonsuz küçükler, sonlu ve sonsuz sayılar için başarılı olan Süreklilik Kuramı ve belirlenemez miktarlar için gösterimi değiştirmenin yönteminin sadece belirlenebilir olanları göstererek yapılacağını anlatan Aşkın Homojenite Yasası gibi bulgusal prensiplere dayanmaktaydı. 18. Yüzyıl sonsuz küçüklerin Leonard Euler ve Joseph-Louis Lagrange gibi matematikçiler tarafından sıklıkla kullanıldığı bir zaman aralığı olmuştur. Augustin-Louis Cauchy sonsuz küçükleri Cour d’Analyse adlı eserinde sürekliliği açıklamak için ve Dirac delta fonksiyonunun ilk formlarından birini tanımlarken kullanmıştır. Tıpkı Cantor ve Dedekind’ın Stevin’in sürekliliğinin daha soyut bir halini geliştirdikleri gibi Paul du Bois-Reymond da sonsuz küçük ile zenginleştirilmiş süreklilik üzerine fonksiyonların artış oranını temel alan bir seri çalışma yapmıştır. Du Bois-Reymond’un çalışması Emile Boral ve Thoralf Skolem’ e ilham verdi. Borel Bois-Reymond’un çalışmalarını Cauchy’nin sonsuz küçüklerin artış oranına dair çalışmalarıyla bağlantı kurdu. Skolem 1934’te aritmetiğin standart dışı ilk modellerini geliştirdi. Süreklilik ve sonsuz küçük yasalarının matematiksel “implementasyonu” Abraham Robinson tarafından 1961’de yapılmıştır. Robinson ayrıca Edwin Hewirr’in 1948’de ve Jerzy Łoś’un 1955’teki çalışmalarına dayanarak standart dışı analizi geliştirmiştir. Hipergerçekler sonsuz küçük ile zenginleştirilmiş sürekliliği sağlar ve transfer prensibi de Leibniz’in süreklilik yasasını sağlar.

Friedrich Hermann Otto Finsch Alman etnograf, doğa tarihçisi ve kâşiftir.

Historia Augusta 117 ila 284 döneminin Roma imparatorları ile onların kıdemsiz belirlenmiş mirasçıları ile gaspçılarının hayatlarının Latince yazılmış geç bir Roma koleksiyonudur. Diocletianus ve I. Konstantin hükümdarlığı döneminde yazılan ve Roma'daki bu imparatorlara veya diğer önemli şahsiyetlere hitap eden altı farklı yazarın eserlerinin bir derlemesi olan Sözde Suetonius'un benzer çalışması De Vita Caesarum üzerinde modellenmiştir. Koleksiyon, mevcut haliyle, çoğu tek bir imparatorun yaşamını içeren otuz biyografiyi içerirken, bazıları sadece bu imparatorların benzer veya çağdaş olduğu için birlikte gruplandırılmış iki veya daha fazla grup içerir.
Gaius Julius Hyginus, M.Ö. 64 ile M.S. 17 yılları arasında yaşamış oyun yazarıdır. Alexander Polyhistor'un öğrencisi ve Augustus'un azatlısıdır. Suetonius'un De Grammaticis'inde yazdığına göre, Augustus tarafından Palatine kütüphanesinin yöneticiliğine atanmıştır. Yine Suetonius'a göre ilerleyen yaşlarda sefalete düşmüş ve Clodius Licinus'un maddi desteği ile hayatına devam edebilmiştir.

Matematik tarihi, öncelikle matematikteki keşiflerin kökenini araştıran ve daha az ölçüde ise matematiksel yöntemleri ve geçmişin notasyonunu araştıran bir bilimsel çalışma alanıdır. Modern çağdan ve dünya çapında bilginin yayılmasından önce, yeni matematiksel gelişmelerin yazılı örnekleri yalnızca birkaç yerde gün ışığına çıktı. MÖ 3000'den itibaren Mezopotamya eyaletleri Sümer, Akad, Asur, Eski Mısır ve Ebla ile birlikte vergilendirmede, ticarette, doğayı anlamada, astronomide ve zamanı kaydetmede/takvimleri formüle etmede aritmetik, cebir ve geometri kullanmaya başladı.

Skald veya skáld (Eski İskandinav : [ˈSkald], sonra [ˈSkɒːld] ; İzlandacada: "Şair" anlamına gelen, genellikle Viking Çağı, MS 793-1066'da İskandinav liderlerinin mahkemelerinde beste yapan ve Orta Çağ'a kadar devam eden şairler için kullanılan bir terimdir. Skaldik şiir, Eski İskandinav şiirinin iki ana grubundan birini oluşturur, diğeri ise anonim Eddic şiiridir.

Aias Lokris kralı Oileus'un oğlu olan mitolojik bir Yunan kahramanıydı. Onu, Telamon oğlu Aias'dan ayırt etmek için, "Küçük" veya "Lokrisli" Aias olarak anıldı. Truva Savaşı sırasında Lokris birliğinin lideriydi. Homeros'un İlyada'sında önemli bir karakterdir ve Odysseia'da, Virgilius'un Aeneis'sinde ve Euripides'in Troyalı Kadınlar'ında da adı geçmektedir. Etrüsk mitolojisinde Aivas Vilates olarak bilinirdi.

Filoktetes (Philoktētēs) veya Philoctetes Yunan mitolojisinde, Teselya'daki Meliboea kralı Poeas'ın oğludur. Annesi Demonnasa veya Methone'dir. Ünlü bir Yunan kahramanıydı, okçu olması ile ünlenmişti ve Truva Savaşı'na katıldı.
John Pediasimos, John Pothos olarak da bilinir, Konstantinopolis, Ohri ve Selanik'te faaliyet gösteren Bizanslı bir kilise görevlisi, bilgin, astronom, matematikçi, mitolog, kıyasçı, müzisyen ve hekimdir.
Marcus Junius Nipsus, 2. yüzyılda yaşamış Romalı bir gromatik yazarıdır ve çeşitli matematiksel sorularla da ilgilenmiştir. Günümüze ulaşan yazıları, MS 4. veya 5. yüzyıllarda arazi ölçümü üzerine yapılan Latince çalışmaların bir derlemesi olan Corpus Agrimensorum Romanorum'da korunmuştur.















