İçeriğe atla

Homolojik cebir

Homolojik cebirin temel bir sonucu olan yılan lemmasında kullanılan bir diyagram.

Homolojik cebir, homolojiyi genel cebirsel ortamda inceleyen matematiğin bir dalıdır. Kökenleri, özellikle Henri Poincaré ve David Hilbert tarafından 19. yüzyılın sonlarında kombinatoryal topoloji (cebirsel topolojinin öncüsü) ve soyut cebir (modüller ve syzygies teorisi) araştırmalarına dayanan nispeten genç bir disiplindir.

Homolojik cebir, homolojik işlevlerin ve bunların gerektirdiği karmaşık cebirsel yapıların incelenmesidir. Gelişimi, kategori teorisinin ortaya çıkışıyla iç içe geçerek ilerlemiştir. Merkezi bir kavram da, hem homolojileri hem de kohomolojileri aracılığıyla incelenebilen zincir kompleksleridir.

Homolojik cebir, bu komplekslerde yer alan bilgileri ayıklamak ve bunu halkaların, modüllerin, topolojik uzayların ve diğer 'somut' matematiksel nesnelerin homolojik değişmezleri biçiminde sunmak amacıyla araçlar sağlar. Bunu yapmak için güçlü bir araç spektral dizilerle sağlanır.

Cebirsel topolojide büyük bir rol oynamıştır. Etkisi kademeli olarak genişlemiş ve günümüzde değişmeli cebir, cebirsel geometri, cebirsel sayı teorisi, temsil teorisi, matematiksel fizik, operatör cebirleri, karmaşık analiz ve kısmi diferansiyel denklemler teorisini içermektedir. <i id="mwKA">K</i> -teorisi, Alain Connes'in değişmeli olmayan geometrisinde olduğu gibi homolojik cebir yöntemlerinden yararlanan bağımsız bir disiplindir.

Kaynakça

  • Henri Cartan, Samuel Eilenberg, Homolojik cebir . David A. Buchsbaum'un eki ile. 1956 orijinalinin yeniden baskısı. Matematikte Princeton Simgesel Yapıları. Princeton University Press, Princeton, NJ, 1999. xvi+390 pp.0-691-04991-2ISBN 0-691-04991-2
  • Saunders Mac Lane, Homoloji . 1975 baskısının yeniden basımı. Matematikte Klasikler. Springer-Verlag, Berlin, 1995. x+422 s.3-540-58662-8ISBN 3-540-58662-8
  • peter hilton ; Stammbach, U. Homolojik cebirde bir kurs . İkinci baskı. Matematik Lisansüstü Metinleri, 4. Springer-Verlag, New York, 1997. xii+364 s.0-387-94823-6ISBN 0-387-94823-6
  • Gelfand, Sergei I.; Yuri Manin, Homolojik cebir yöntemleri . Rusça 1988 baskısından çevrilmiştir. İkinci baskı. Matematikte Springer Monografları. Springer-Verlag, Berlin, 2003. xx+372 s.3-540-43583-2ISBN 3-540-43583-2
  • Gelfand, Sergei I.; Yuri Manin, Homolojik cebir . Yazarlar tarafından 1989 tarihli Rusça orijinalinden çevrilmiştir. Encyclopaedia of Mathematical Sciences (Cebir, V, Encyclopaedia Math. Sci., 38, Springer, Berlin, 1994). Springer-Verlag, Berlin, 1999. iv+222 s.3-540-65378-3ISBN 3-540-65378-3
  • 978-0-521-55987-4

İlgili Araştırma Makaleleri

<span class="mw-page-title-main">Matematik</span> nicelik, yapı, uzay ve değişim gibi konularla ilgilenen bilim dalı

Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.

<span class="mw-page-title-main">Leopold Kronecker</span> Sayılar teorisi ve cebir üzerine çalışan Alman matematikçi (1823-1891)

Leopold Kronecker sayı teorisi, cebir ve mantık üzerine çalışan bir Alman matematikçiydi. Georg Cantor'un küme teorisi üzerine çalışmalarını eleştirdi ve Weber (1893) tarafından "Almanca: Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk " söylemiyle alıntılandı. Kronecker, Ernst Kummer'in öğrencisi ve ömür boyu arkadaşıydı.

Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.

<span class="mw-page-title-main">Soyut cebir</span> Matematiğin bir alanı

Soyut cebir veya soyut matematik, matematiğin bir alanı olup, cebirsel yapılar üzerinde çalışır. Cebirsel yapılar, elemanları üzerinde belirli işlemlerin uygulandığı kümelerdir ve gruplar, halkalar, alanlar, modüller, vektör uzayları, kafesler ve alan üzerindeki cebirler içerir. Soyut cebir terimi, 20. yüzyılın başlarında temel cebirden ayırmak amacıyla türetilmiştir. Soyut cebir ileri matematik için temel hale geldikçe basitçe "cebir" olarak adlandırılırken, "soyut cebir" terimi pedagoji dışında nadiren kullanılır.

Ayşe Soysal Türk matematikçi.

Cebirsel geometri, matematiğin bir dalıdır. Adından anlaşılabileceği gibi, soyut cebirin, özellikle değişmeli cebirin yöntemleri ile geometrinin dili ve problemlerini bir araya getirir. Çağdaş matematik içerisinde merkezi bir rol üstlenmesinin yanında, karmaşık analiz, topoloji, sayılar kuramı gibi matematiğin diğer dallarıyla yakın ilişkisi vardır.

<span class="mw-page-title-main">Cebirsel topoloji</span>

Cebirsel topoloji, topolojik uzayları cebirsel gereç ve yöntemlerle inceleyen matematik dalı. Matematikte bir kümenin üzerine döşenecek yapı, yönelinen matematik dalını belirler. Bir kümeye bir ya da birkaç işlem konarak sayılar kuramı ya da cebir yapmaya başlanabilir. Kümenin üzerine bir topoloji koyaraksa topoloji ve, ayrıca uzunluk koyarsak, geometri yapmaya başlanır. Üzerine topoloji konmuş bir uzayı incelemek için kimi cebirsel, aritmetik veya topolojik değişmezler tanımlanır; bunlar aracılığıyla topolojik uzayın özellikleri ayırdedilir. Örneğin tıkızlık, bağlantılılık, sayılabilirlik bu tür değişmezlerdir. Topolojik eşyapısal iki uzaydan biri bu değişmeze sahipse diğeri de buna sahip olmalıdır. Yani, eğer iki uzay için ayrı ayrı bakılan bir değişmez aynı değilse, bu iki uzay eşyapısal olmayacaktır. Yukarıda anılan en eski değişmezlerin hemen ardından inşa edilen klasik değişmezler cebirsel olanlardır.

Şablon:Group theory sidebar

Matematikte, Lie grupları teorisi Şablon:Harvard alıntıs. tarafından Lie grupları üzerinde bir kitap serisidir.

Tarih boyunca matematiğin konu çeşitliliği ve derinliği artmaktadır, matematiği kavrama, birçok konuyu matematiğin daha genel alanlarına göre sınıflandırma ve düzenleme için bir sistem gerektirir. Bir dizi farklı sınıflandırma şeması ortaya çıkmıştır ve bazı benzerlikleri paylaşsalar da, kısmen hizmet ettikleri farklı amaçlara bağlı olarak farklılıkları vardır. Ek olarak, matematik geliştirilmeye devam ettikçe, bu sınıflandırma şemaları da yeni oluşturulan alanları veya farklı alanlar arasında yeni keşfedilen bağlantıları dikkate alacak şekilde değişmelidir. Farklı alanlar arasındaki sınırı aşan, genellikle en aktif olan bazı konuların sınıflandırılması daha zor hale gelir.

Bu sayfa teoremlerin bir listesidir. Ayrıca bakınız:

<span class="mw-page-title-main">Israel Gelfand</span> Sovyet matematikçi (1913 – 2009)

Israel Moyseyovich Gelfand, Yahudi asıllı ünlü bir Sovyet matematikçisiydi. Grup teorisi, temsil teorisi ve fonksiyonel analiz dahil olmak üzere matematiğin birçok dalına önemli katkılarda bulundu. Lenin Nişanı ve ilk Kurt Ödülü de dahil olmak üzere birçok ödülün sahibi, Kraliyet Cemiyeti'nin Yabancı Üyesi ve Moskova Devlet Üniversitesi'nde profesördü ve 76. doğum gününden kısa bir süre önce Rutgers Üniversitesi'nde Amerika Birleşik Devletleri'ne göç etti ve yaşamının sonuna dek orada kaldı.

<span class="mw-page-title-main">Jean-Pierre Serre</span> Fransız matematikçi (d. 1926)

Jean-Pierre Serre cebirsel topoloji, cebirsel geometri ve cebirsel sayı teorisine katkıda bulunan Fransız matematikçidir. 1954'te Fields Madalyası, 2000'de Wolf Ödülü ve 2003'te açılış Abel Ödülü'ne layık görüldü.

Bu Rus matematikçiler listesi, Rusya İmparatorluğu, Sovyetler Birliği ve Rusya Federasyonu'ndan ünlü matematikçileri içermektedir.

Türk Matematik Dergisi, Turkish Journal of Mathematics, Türkiye Bilimsel ve Teknolojik Araştırma Kurumu (TÜBİTAK) tarafından elektronik ortamda ve iki ayda bir yayınlanan, açık erişimli, hakemli akademik bir dergidir. Derginin amacı, ortak bir akademik platform sağlayarak araştırma kültürünü geliştirmek ve bilginin akademik dünyada hızla yayılmasına yardımcı olmaktır. Turkish Journal of Mathematics'de yayınlanan tüm yazılar CC BY 4.0 ile lisanslanmıştır. Gönderim ve yayın ücretsizdir. İngilizce olarak yayınlanır ve journals.tubitak.gov.tr ve dergipark.org.tr/tr/ adreslerinden ücretsiz olarak erişilebilir. Makaleler ayrıca her zaman bulunabilmelerini sağlamak için CrossRef organizasyonundan Dijital Nesne Tanımlayıcıları (DOI'ler) alır. Dergi, araştırma makalelerinin ve inceleme makalelerinin yayınlarını kabul eder. Dergi, matematiğin geniş yelpazesi hakkında kritik ve güncel bilgiler sağlayan kapsamlı bir kaynaktır.

<span class="mw-page-title-main">Yuri Manin</span> Rus matematikçi (1937–2023)

Yuri İvanoviç Manin, cebirsel geometri ve diyofant geometri alanındaki çalışmaları ve matematiksel mantıktan teorik fiziğe kadar birçok açıklayıcı çalışmasıyla tanınmış bir Rus matematikçidir. Ayrıca Manin, 1980 yılında Computable and Uncomputable adlı kitabıyla kuantum bilgisayar fikrini ilk önerenlerden birisidir.

<span class="mw-page-title-main">Değişmeli cebir</span>

İlk olarak ideal teori olarak bilinen Komütatif (değişmeli) cebir, cebirin değişmeli halkalarını, halkaların ideallerini ve bu halkalar üzerindeki modülleri inceleyen dalıdır. Hem cebirsel geometri hem de cebirsel sayı teorisi değişmeli cebire dayanır. Değişmeli halkaların öne çıkan örnekleri arasında polinom halkaları; sıradan tamsayılar dahil olmak üzere cebirsel tam sayı halkaları  ; ve p -sel tam sayıları içerir.

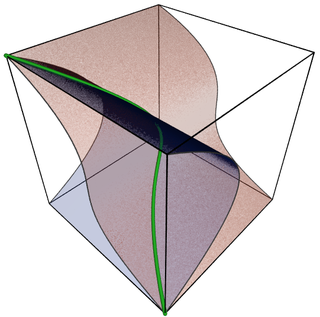
<span class="mw-page-title-main">Cebirsel varyete</span>

Cebirsel varyeteler, matematiğin bir alt alanı olan cebirsel geometride çalışmanın ana nesneleridir. Klasik olarak cebirsel çeşitlilik, bir polinom denklem sisteminin gerçek veya karmaşık sayılar üzerindeki çözüm kümesi olarak tanımlanır. Modern tanımlamalar orijinal tanımın arkasındaki geometrik sezgiyi korumaya çalışırken kavramı birkaç farklı şekilde genelleştirir.

Matematikte homoloji, değişmeli gruplar veya modüller gibi bir dizi cebirsel nesneyi topolojik uzaylar gibi matematiksel nesnelerle ilişkilendirmenin genel bir yoludur. Homoloji grupları özgün olarak cebirsel topolojide tanımlanmıştır. Soyut cebir, gruplar, Lie cebirleri, Galois teorisi ve cebirsel geometri gibi çok çeşitli başka alanlarda da benzer yapılar mevcuttur.

Cebirde halka teorisi, toplama ve çarpmanın tanımlandığı ve tamsayılar için tanımlanan işlemlere benzer özelliklere sahip cebirsel yapılar olan halkaların incelenmesidir. Halka teorisi; halkaların yapısını, temsillerini veya farklı dillerde modülleri, özel halka sınıflarını ve homolojik özellikler ve polinom özdeşlikleri gibi uygulamaları inceler.


Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.