
Küresel koordinat sistemi, üç boyutlu uzayda nokta belirtmenin bir yoludur.

Öz direnç (Empedans), maddenin kimyasal özelliğinden dolayı direncinin artması ya da azalmasına neden olan her maddeye özgü ayırt edici bir özelliktir. Farklı maddelerin empedansları aynı olabilir ama öz dirençleri aynı olamaz. R= Lq/Q dur. (Rezistif Direnç= Uzunluk*öz direnç/kesit, Alternatif akım'a karşı koyan zorluk olarak adlandırılır. İçinde kondansatör ve endüktans gibi zamanla değişen değerlere sahip olan elemanlar olan devrelerde direnç yerine öz direnç kullanılmaktadır. Öz direnç gerilim ve akımın sadece görünür genliğini açıklamakla kalmaz, ayrıca görünür fazını da açıklar. DA devrelerinde öz direnç ile direnç arasında hiçbir fark yoktur. Direnç sıfır faz açısına sahip öz direnç olarak adlandırılabilir.

Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.

Matematikte gül veya rodonea, kutupsal koordinat sisteminde çizilmiş bir sinüs ya da kosinüs eğrisine denir. Gül eğrisi, aşağıdaki kutupsal denklemle ifade edilir:

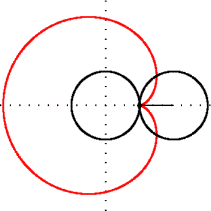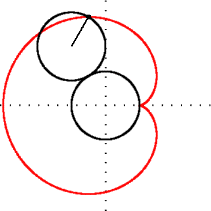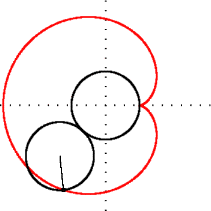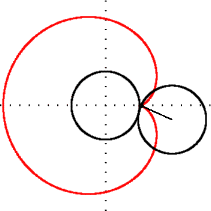
Matematikte kardiyoit veya yürek eğrisi, sabit bir çember üzerinde yuvarlanmakta olan aynı yarıçaplı ikinci bir çember üzerindeki herhangi bir noktanın izlediği eğridir. İsmi Yunanca kardia (kalp) ve eidos (şekil) kelimelerinin birleşiminden oluşur. Kalp (♥) şeklini anımsattığı için bu ismi almıştır. Kardiyoit ismini ilk kullanan, 18. yüzyıl İtalyan matematikçisi Johann Castillon olmuştur.

Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda potansiyel teorisi olarak da bilinmektedir.

Euler spirali, eğimi eğrinin uzunluğuyla doğrusal olarak degişen bir eğridir. Euler spiralleri yaygın olarak spiros, clothoids veya Cornu spiralleri olarak da adlandırılır. Euler spirallerinin kırınım hesaplamalarında uygulamaları vardır. Genellikle demiryolu ve karayolu mühendisliklerinde teğet eğrisi ve dairesel eğri arasındaki geometriyi bağdaştırmaya ve aktarmaya yarayan geçiş eğrisi olarak kullanılır. Teğet eğrisi ve dairesel eğri arasındaki geçiş eğrisinin eğimindeki lineer değişim prensibi Euler spiralinin geometrisini belirler:
- Eğimi teğetin düzgün kesitinden başlayarak lineer olarak eğri boyunca artar.
- Euler spiralinin dairesel eğriyle karşılaştığı yerde eğimi dairesel eğrinin eğimine eşit olur.
Burada, en yaygın olarak kullanılan koordinat dönüşümü bazılarının bir listesi verilmiştir. Kısmi türevler alınırken çarpımın türevi gibi davranıldığı akıldan çıkarılmamalıdır. Bir örnek olarak  fonksiyonunda üç çarpım vardır
fonksiyonunda üç çarpım vardır
Değişken değiştirme, İntegral, çarpanlara ayırma, denklemler, üslü denklemler, trigonometri ve diferansiyel denklemler başta olmak üzere matematiğin her alanında işlemi basitleştirmek için kullanılan matematiksel bir yöntemdir.
Matematiksel fizikte, hareket denklemi, fiziksel sistemin davranışını, sistem hareketinin zamanı ve fonksiyonu olarak tanımlar. Daha detaya girmek gerekirse; hareket denklemi, matematiksel fonksiyonların kümesini "devinimsel değişkenler" cinsinden izah eder. Normal olarak konumlar, koordinat ve zaman kullanılır ama diğer değişkenler de kullanılabilir: momentum bileşenleri ve zaman gibi. En genel seçim genelleştirilmiş koordinatlardır ve bu koordinatlar fiziksel sistemin karakteristiğinin herhangi bir uygun değişkeni olabilirler. Klasik mekanikte fonksiyonlar öklid uzayında tanımlanmıştır ama görelilikte öklid uzayı, eğilmiş uzay ile tanımlanmıştır. Eğer sistemin dinamiği biliniyor ise denklemler dinamiğin hareketini izah eden diferansiyel denklemlerin çözümleri olacaktır.

Gök mekaniği olarak, Kepler yörüngesi üç boyutlu uzayda iki boyutlu bir yörünge düzlemi oluşturan bir elips, parabol, hiperbol benzeri bir yörünge cismininin hareketini açıklar.. Kepler yörüngesi yalnızca nokta iki cismin nokta benzeri yerçekimsel çekimlerini dikkate alır, atmosfer sürüklemesi, güneş radyasyonu baskısı, dairesel olmayan cisim merkezi ve bunun gibi bir takım şeylerin diğer cisimlerle girdiği çekim ilişkileri nedeniyle ihmal eder. Böylece Kepler problemi olarak bilinen iki-cisim probleminin, özel durumlara bir çözüm olarak atfedilir. Klasik mekaniğin bir teorisi olarak, aynı zamanda genel görelilik etkilerini dikkate almaz. Kepler yörüngeleri çeşitli şekillerde altı yörünge unsurları içine parametrize edilebilir.

Öklid geometrisinde, Batlamyus teoremi, bir kirişler dörtgeninin dört kenarı ile iki köşegeni arasındaki bir ilişkiyi gösteridir. Teorem, Yunan astronom ve matematikçi Batlamyus'un adını almıştır. Batlamyus, teoremi astronomiye uyguladığı trigonometrik bir tablo olan kirişler tablosunu oluşturmaya yardımcı olarak kullandı.

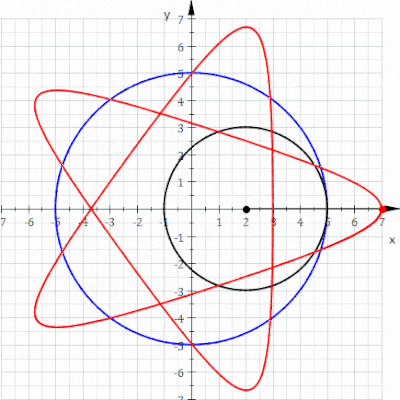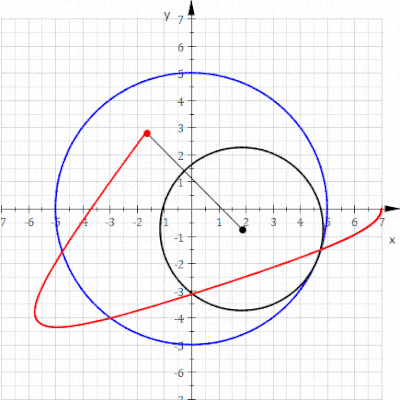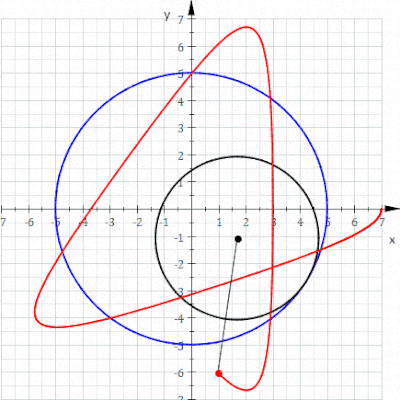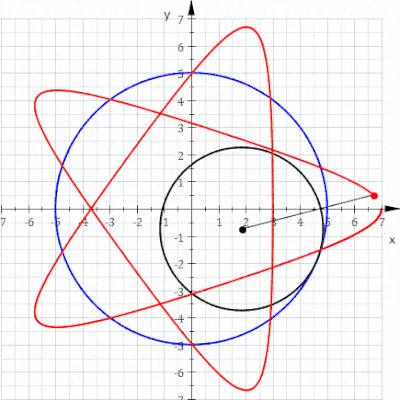
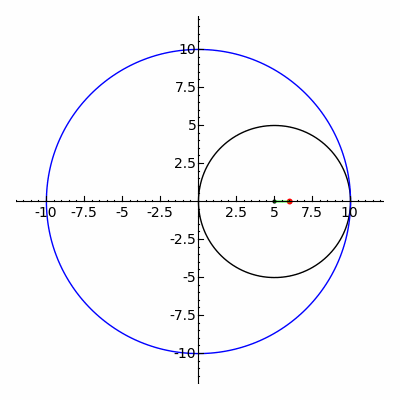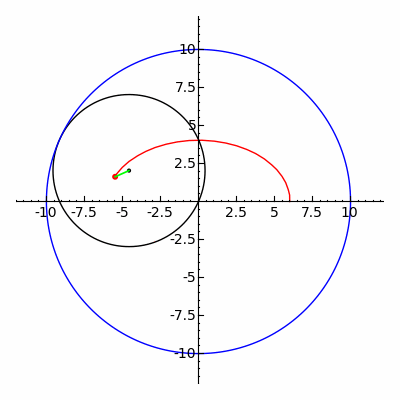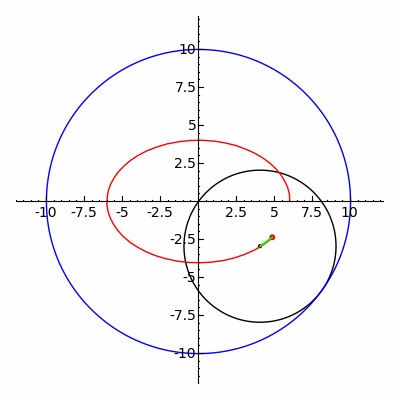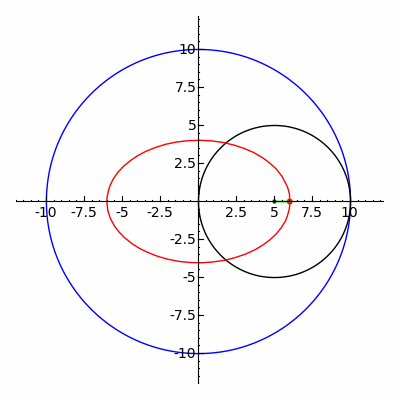
Geometride, bir epitrokoid, yarıçapı R olan sabit bir çemberin dış çevresinde dönen r yarıçaplı çembere bağlı bir nokta tarafından izlenen bir yuvarlanma eğrisi olup, nokta dış çemberin merkezinden d uzaklıktadır.
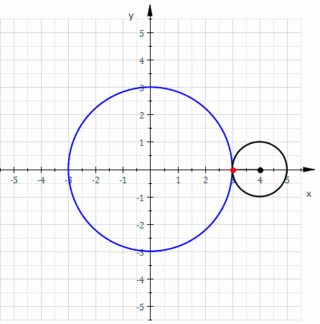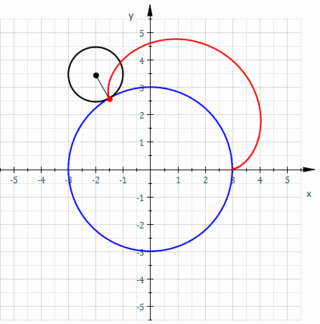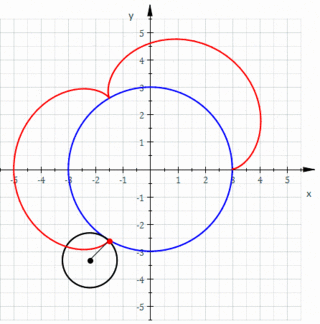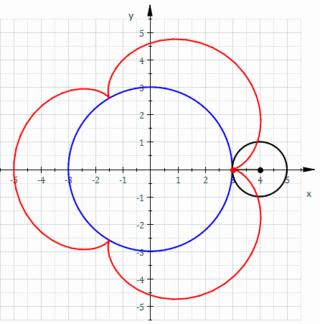
Geometride, bir episikloid, sabit bir çemberin etrafında kaymadan yuvarlanan bir çemberin çevresi üzerinde seçilen bir noktanın yolunu izleyerek üretilen bir düzlem eğrisidir -buna episikl (epicycle) denir. Bu, yuvarlanma eğrisinin özel bir türüdür.

Matematikte, bir parametrik denklem, bir grup niceliği parametreler olarak adlandırılan bir veya daha fazla bağımsız değişkenin fonksiyonları olarak tanımlar. Parametrik denklemler genellikle bir eğri veya yüzey gibi geometrik bir nesneyi oluşturan noktaların koordinatlarını ifade etmek için kullanılır ve sırasıyla parametrik eğri ve parametrik yüzey olarak adlandırılır. Bu gibi durumlarda, denklemler, toplu olarak nesnenin parametrik temsili veya parametrik sistem, veya parametrelendirilmesi olarak adlandırılır.
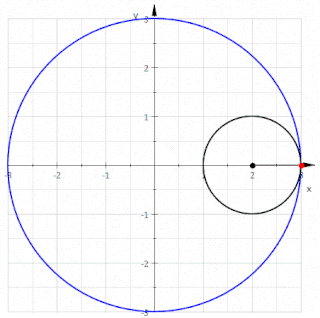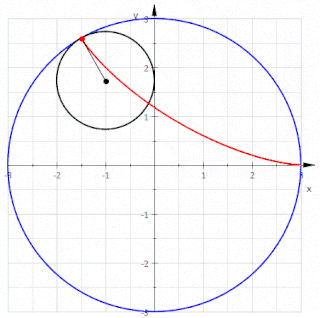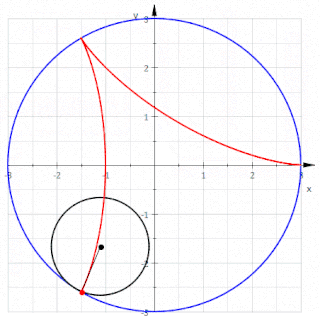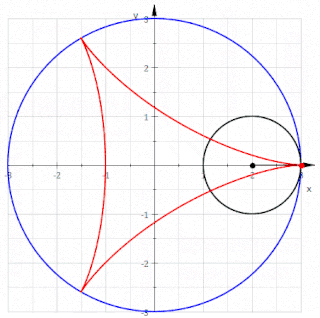
Geometride, triküspoid eğri veya Steiner eğrisi olarak da bilinen deltoid eğri, üç çentikten oluşan bir hiposikloiddir. Başka bir deyişle, bir çemberin çevresi üzerindeki bir noktanın, yarıçapının üç veya bir buçuk katı olan bir çemberin içinde kaymadan yuvarlanırken oluşturduğu yuvarlanma eğrisidir. Adını, benzediği büyük Yunanca delta (Δ) harfinden alır.

Karmaşık analizde Casorati-Weierstrass teoremi, holomorf fonksiyonların esaslı tekillikler civarındaki olağanüstü davranışlarını açıklayan bir ifadedir. Teorem, Karl Theodor Wilhelm Weierstrass ve Felice Casorati'ye atfen isimlendirilmiştir.
Trigonometride, trigonometrik özdeşlikler trigonometrik fonksiyonları içeren ve eşitliğin her iki tarafının da tanımlandığı değişkenlerin her değeri için doğru olan eşitliklerdir. Geometrik olarak, bunlar bir veya daha fazla açının belirli fonksiyonlarını içeren özdeşliklerdir. Bunlar üçgen özdeşliklerinden farklıdır, bunlar potansiyel olarak açıları içeren ama aynı zamanda kenar uzunluklarını veya bir üçgenin diğer uzunluklarını da içeren özdeşliklerdir.
Trigonometrik fonksiyonları tanımlamanın birkaç eşdeğer yolu vardır ve bunlar arasındaki trigonometrik özdeşliklerin kanıtları seçilen tanıma bağlıdır. En eski ve en temel tanımlar dik üçgenlerin geometrisine ve kenarları arasındaki orana dayanır. Bu makalede verilen kanıtlar bu tanımları kullanır ve dolayısıyla bir dik açıdan büyük olmayan negatif olmayan açılar için geçerlidir. Daha büyük ve negatif açılar için Trigonometrik fonksiyonlar bölümüne bakınız.
 . Dover Publications. ss. 165-168. ISBN 0-486-60288-5.
. Dover Publications. ss. 165-168. ISBN 0-486-60288-5.
























