
Bir üçgen düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir. Üçgene müselles ve üçbucak da denir.

Ceva Teoremi, herhangi bir ABC üçgeni verildiğinde, A, B ve C'den üçgenin zıt kenarlarına doğru olan doğru parçalarının üçgenin her iki kenarında oluşan doğru parçası çiftlerinin oranlarının çarpımı 1'e eşit olduğunda tek noktada kesiştiğini belirtir. Teorem adını İtalyan matematikçi Giovanni Ceva'dan alır.

Açıortay, geometride bir açıyı iki eşit açı şeklinde bölen yapıdır. Bir açıya teğet tüm çemberler çizilerek merkezleri birleştirilirse, o açının açıortayı elde edilir. Bu nedenle açıortaylardan açının kollarına indirilen dikmeler, o çemberlerden birinin merkezinden teğetlere inilen yarıçap dikmeleri olacağından, dikmeler birbirine eşit olur. Her iki kolda oluşan üçgenler de birbirine eşit olacağından, dikmelerin açıortay kollarını kestiği noktalar ile açının bulunduğu köşeye olan uzaklıklar eşit olur.

Çemberlerde Thales teoremi, alınan A, B ve C noktalarının bir çember üzerinde ve AC doğrusunun bu çemberin çapı olması durumunda, ABC açısının dik açı olacağını belirten geometri teoremi. Thales teoremi çevre açı kurallarının özel bir hâlidir. Adını Thales'ten alan teorem, genellikle ona atfedilir ancak bazı yerlerde Pisagor'la da ilişkilendirilir.

Geometride, Thales teoremi, A, B ve C, AC çizgisinin bir çap olduğu bir daire üzerinde farklı noktalar ise, ∠ABC açısının bir dik açı olduğunu belirtir. Thales teoremi, çevre açı teoreminin özel bir durumudur ve Öklid'in Elemanlar adlı eserinin üçüncü kitabında 31. önermenin bir parçası olarak bahsedilmiş ve kanıtlanmıştır. Genellikle, teoremin keşif için şükran kurbanı olarak bir öküz sunduğu söylenen Miletli Thales'e atfedilir, ancak bazen Pisagor'a da atfedilir.

Pappus'un alan teoremi, verilen herhangi bir üçgenin üç kenarına yaslanmış üç paralelkenarın alanları arasındaki ilişkiyi tanımlar. Pisagor teoreminin bir genellemesi olarak da düşünülebilecek teorem, adını onu keşfeden Yunan matematikçi İskenderiyeli Pappus'tan almıştır.

Öklid geometrisinde, Batlamyus teoremi, bir kirişler dörtgeninin dört kenarı ile iki köşegeni arasındaki bir ilişkiyi gösteridir. Teorem, Yunan astronom ve matematikçi Batlamyus'un adını almıştır. Batlamyus, teoremi astronomiye uyguladığı trigonometrik bir tablo olan kirişler tablosunu oluşturmaya yardımcı olarak kullandı.
Carnot teoremi, bir üçgenin iç teğet çemberi ve çevrel çemberinin yarıçaplarının uzunlukları ile çevrel çemberin merkezinden üçgenin üç kenarına olan mesafelerin toplamı arasındaki ilişkiyi göstermektedir. Fransız matematikçi Lazare Nicolas Marguerite Carnot tarafından bulunmuştur.
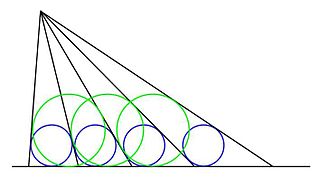
Geometride, eş iç teğet çemberler teoremi bir Japon Sangaku'sundan türetilir ve aşağıdaki yapıya ilişkindir: belirli bir noktadan belirli bir çizgiye bir dizi ışın çizilir, öyle ki bitişik ışınlar ve taban çizgisi tarafından oluşturulan üçgenlerin iç teğet çemberleri eşittir. Çizimde eş mavi çemberler, açıklandığı gibi ışınlar arasındaki mesafeyi tanımlar.

Adını Fransız matematikçi Lazare Carnot'dan alan Carnot teoremi, üçgenin (uzatılmış) kenarlarına dik olan üç doğrunun ortak bir kesişme noktası için gerek ve yeter koşulu tanımlar. Teorem ayrıca Pisagor teoreminin bir genellemesi olarak düşünülebilir.

Adını Fransız matematikçi Jean Paul de Gua de Malves'den alan De Gua teoremi, Pisagor teoreminin üç boyutlu bir analojisidir.

Üçgen geometrisinde, üçgenin iç çemberi ve dokuz nokta çemberi, üçgenin Feuerbach noktasında birbirine içten teğettir. Feuerbach noktası bir üçgen merkezidir, yani tanımı üçgenin yerleşimine ve ölçeğine bağlı değildir. Clark Kimberling'in Üçgen Merkezleri Ansiklopedisi'nde X(11) olarak listelenmiştir ve adını Alman geometrici Karl Wilhelm Feuerbach'tan almıştır.

Öklid geometrisinde, bir çift merkezli dörtgen, hem bir iç teğet çembere hem de çevrel çembere sahip olan bir dışbükey (konveks) dörtgendir. Bu çemberlerin çevreleri, yarıçapları ve merkezlerine sırasıyla iç çap (inradius) ve çevrel çap (circumradius), iç merkez (incenter) ve çevrel merkez (circumcenter) denir. Tanımdan, çift merkezli dörtgenlerin hem teğetler dörtgeninin hem de kirişler dörtgeninin tüm özelliklerine sahip olduğu anlaşılmaktadır. Bu dörtgenler için diğer isimler kiriş-teğet dörtgeni ve iç teğet ve dış teğet dörtgenidir. Ayrıca nadiren çift çemberli dörtgen ve çift işaretlenmiş dörtgen olarak adlandırılmıştır.

Dik üçgen yükseklik teoremi veya geometrik ortalama teoremi, bir dik üçgendeki hipotenüs üzerindeki yükseklik uzunluğu ile hipotenüs üzerinde oluşturduğu iki doğru parçası arasındaki ilişkiyi tanımlayan temel geometrinin bir sonucudur. İki doğru parçasının geometrik ortalamasının yüksekliğe eşit olduğunu belirtir.

Geometride, çevre açı, çember üzerinde iki sekant (kesen) çizgisi kesiştiğinde bir çember üzerinde oluşan açıdır. Çember üzerindeki bir nokta ile çember üzerinde verilen diğer iki noktanın oluşturduğu açı olarak da tanımlanabilir.

Kesişen kirişler teoremi veya sadece kiriş teoremi, bir çember içinde kesişen iki kiriş tarafından oluşturulan dört doğru parçasının ilişkisini tanımlayan temel geometrideki bir ifadedir. Her bir kirişteki doğru parçalarının uzunluklarının çarpımlarının eşit olduğunu belirtir. Öklid'in Unsurlarının 3. kitabının 35. önermesidir.

Kesişen kesen (sekant) teoremi veya sadece kesen (sekant) teoremi, kesişen iki sekant ve ilişkili çember tarafından oluşturulan doğru parçalarının ilişkisini açıklayan temel bir geometri teoremidir.
Geometride, bir çokgenin yarı çevresi, çevre uzunluğunun yarısıdır. Çevreden doğrudan türetilebilmesine rağmen, yarı çevre üçgenler ve diğer şekiller için kullanılan formüllerde oldukça sık görülür ve ayrı/özel bir isim verilir. Yarı çevre, bir formülün parçası olarak ortaya çıktığında, genellikle s harfiyle gösterilir.

Temel geometride, Reuschle teoremi, ortak bir noktada kesişen bir üçgenin cevianlarının bir özelliğini tanımlar ve adını Alman matematikçi Karl Gustav Reuschle (1812-1875)'den alır. Ayrıca Fransız matematikçi Olry Terquem (1782-1862)'in adıyla 1842'de yayınlayan Terquem teoremi olarak da bilinir. Teorem, Euler doğrusu ve Feuerbach'ın dokuz nokta çemberi ile bağlantılı olarak benzer biçimde bulunan belirli köşe çaprazlarının kesişim özellikleriyle ilgili bir problemi ele almaktadır. Reuschle teoreminin ispatı, sekant teoreminin yanı sıra Ceva teoremi ve onun karşıt teoremine dayanmaktadır.













































