Görüntü yükleri yöntemi

Görüntü yük yöntemi (görüntü yöntemi, imaj yöntemi veya ayna yükü yöntemi olarak da bilinir), elektrostatikte kullanılan bir soru çözüm tekniğidir. İsimlendirmenin kökeni problemdeki sınır koşullarını (Dirichlet sınır koşulları veya Neumann sınır koşulları) bazı sanal yükler ile değiştirme yönteminden gelir.

Herhangi bir teklik teoremine göre belli şartları çözüm bulunabilirse, bu aynı zamanda o şartlar altında denklemin tanımlanmış tek çözümüdür.

Örnekle açıklamak için kapalı bir çember çizelim. Eğer:

bölgenin içinde ${\displaystyle \nabla ^{2}V=f}$ ve yüzeyde V = g ise

${\displaystyle V(x,y,z)}$ 'tektir (f ve g sabitler verildiğinde).

Bu noktada görüntü yük yöntemine göre sınır şartlarını sağlayan yükler bulunabildiği anda problemden sınırlar kaldırılıp yerine görüntü yükler konulabilir ve bu yalnızca bir şekilde yapılabilir.

Bu yöntemin en basit örneği 2-boyutlu uzayda (0, a) noktasındaki +q yükünün x ekseni boyunca uzanan topraklanmış bir iletken yüzeyle birlikte oluşturduğu sistemdir. Bu sistemden herhangi bir çıkarım yapmak, yük yoğunluğu gibi, basit değildir.

Durumu basitleştirmek adına (0,-a) noktasına bir -q yükü koyarak plaka üzerindeki tüm noktalarda potansiyeli sıfırlayarak istenen sınır koşuluğunu sağlayabiliriz. Bu çözüm bizim sınır koşulumuzu sağladığından teklik teoremine göre tek çözümdür.

Yeni sistem bir öncekine denktir. Bu noktadan itibaren Gauss yasasını kullanarak topraklanmış yüzey üzerinde herhangi bir noktadaki yük dağılımını veya sistemle ilgili başka herhangi bir bilgiyi elde etmek bir önceki sisteme göre oldukça kolay bir hal alır. Silindirik koordinatlarda uzaydaki herhangi bir noktadaki potansiyel:

${\displaystyle V\left(\rho ,\varphi ,z\right)={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{\sqrt {\rho ^{2}+\left(z-a\right)^{2}}}}+{\frac {-q}{\sqrt {\rho ^{2}+\left(z+a\right)^{2}}}}\right)\,}$

Teklik teoreminden dolayı bu elde ettiğimiz çözüm tek çözümdür.

Topraklanmış plaka üzerindeki yük yoğunluğu:

${\displaystyle \sigma =-\epsilon _{0}{\frac {\partial V}{\partial y}}{\Bigg |}_{y=0}\,}$

Sadeleştirmelerden sonra:

${\displaystyle \sigma \left(x\right)={\frac {-qa}{2\pi \left(x^{2}+a^{2}\right)^{3/2}}}\,}$

Buna ek olarak topraklanmış plaka üzerinde indüklenen toplam yük, yük yoğunluğunun o yüzey üzerinde alınmış integraline eşittir:

${\displaystyle {\begin{aligned}Q_{t}&=\int _{0}^{2\pi }\int _{0}^{\infty }\sigma \left(x\right)\,x\,dx\,d\theta \\[6pt]&={\frac {-qa}{2\pi }}\int _{0}^{2\pi }d\theta \int _{0}^{\infty }{\frac {x\,dx}{\left(x^{2}+a^{2}\right)^{3/2}}}\\[6pt]&=-q\end{aligned}}}$

Sonuç olarak beklendiği üzere toplamda topraklanmış plaka üzerinde -q kadar yük indüklenmiş olur.

Bu yöntem 2 veya daha fazla yük için, plakayı bu yüklerin görüntü yükleriyle değiştirilerek genişletilebilir. Bir noktadaki toplam potansiyel o noktadaki potansiyellerin toplamı olduğundan her gerçek yük kendi görüntü yükünün o noktadaki potansiyelini sıfırlayacaktır. Böylece plaka üzerinde herhangi bir noktada potansiyel tam da sınır koşulunun gerektirdiği gibi sıfır olacaktır. Sağdaki şekil bu açılımın özel bir halini gösteriyor. Bu durumda plakadan a kadar yüksekte olan iki gerçek yük var. Eğer topraklanmış yüzeyden h kadar yüksekte yüzeyle θ açısı yapan bir elektrik dipolü varsa yüzey gerçek dipolün ayna simetriği bir başka elektrik dipole ile değiştirilebilir.

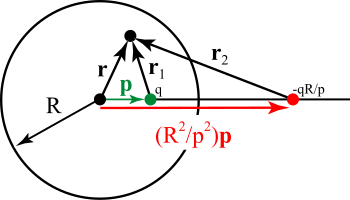
Görüntü yük yöntemi kürelere de uygulanabilirTikhonov 1963. Aslında görüntü yük yönteminin düzleme uygulanması küreye uygulanmış halinin özel bir durumudur. Şekilde bulunmak istenen topraklanmış R yarıçaplı kürenin içinde, kürenin içerisinde${\displaystyle \mathbf {p} }$ konumunda olan yüklü parçacığın oluşturduğu potansiyeldir. Parçacığın yükü q olsun. Bu yükün küreye göre görüntü yükü kırmızı ile gösterilmiştir. Bu görüntü yükün yükü q'=-qR/p olup kürenin merkezi ile kürenin içerisindeki yükün vektörel olarak üzerinde bulunduğu doğrultuda${\displaystyle (R^{2}/p^{2})\mathbf {p} }$ konumunda yer alır. Şekilde görüldüğü gibi${\displaystyle \mathbf {r} }$ yarıçap vektörü ile belirtilen bir noktada bu yüklerden kaynaklanan potansiyel:

${\displaystyle 4\pi \epsilon _{0}V(\mathbf {r} )={\frac {q}{|\mathbf {r} _{1}|}}+{\frac {(-qR/p)}{|\mathbf {r} _{2}|}}={\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}+{\frac {(-qR/p)}{\sqrt {r^{2}+{\frac {R^{4}}{p^{2}}}-{\frac {2R^{2}}{p^{2}}}\mathbf {r} \cdot \mathbf {p} }}}}$

En sağdaki ifade ile çarpıldığında:

${\displaystyle V(\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]}$

ifadeden de görüldüğü gibi küre yüzeyinde (r=R) potansiyel sıfırlanır. Böylece kürenin içerisindeki herhangi bir noktadaki potansiyel bu iki yükün o noktadaki potansiyellerin toplamı ile verilir. Görüntü yükler gerçekte var olmadığından dolay bu potansiyel kürenin dışında geçerli değildir. Kürenin dışındaki potansiyel sadece kürenin dışındaki yük dağılımı ile belirlenir ve kürenin içindeki yük dağılımından bağımsızdır. Basitlik adına içerdeki yükün z ekseninde yer aldığını düşünürsek o zaman indüklenmiş yük yoğunluğu küresel koordinatlarda sadece &theta nın bir fonksiyonu olacaktır:

${\displaystyle \sigma (\theta )=\epsilon _{0}{\frac {\partial V}{\partial r}}{\Bigg |}_{r=R}={\frac {-q(R^{2}-p^{2})}{4\pi R(R^{2}+p^{2}-2pR\cos \theta )^{3/2}}}}$

Küre üzerindeki toplam yük tüm açılar üzerinden integral alınarak bulunabilir:

${\displaystyle Q_{t}=\int _{0}^{\pi }d\theta \int _{0}^{2\pi }d\phi \,\,\sigma (\theta )R^{2}\sin \theta =-q}$

Burada dikkat edilmesi gereken durum karşılıklı problemin de aynı yöntemle çözülebilir olduğudur. Diğer bir deyişle eğer elimizde R yarıçaplı bir kürenin dışında ${\displaystyle \mathbf {p} }$ vektörel konumunda bir q yükü varsa kürenin dışındaki potansiyel aynı şekilde bu gerçek yükün o noktadaki potansiyeli ile bu yükün görüntüsünün o noktadaki potansiyelinin toplamı olarak verilebilir. Aynı durum benzer şekilde küre üzerindeki yük dağılımı için de geçerlidir.

Öte yandan bir elektrik dipolünün görüntüsü biraz daha karmaşıktır. Eğer dipol birbirinden küçük bir mesafeyle ayrılmış 2 zıt yük olarak tasvir edilirse o zaman dipolün görüntüsü sadece yüklerin görüntülenmesinin yanı sıra aralarındaki mesafenin de modifiye edilmesini kapsayacaktır. Sonuç olarak ${\displaystyle \mathbf {p} }$ konumundaki bir elektrik dipolünün görüntüsü ${\displaystyle (R^{2}/p^{2})\mathbf {p} }$ konumunda olacak ve yükler için:

${\displaystyle q'={\frac {R\mathbf {p} \cdot \mathbf {M} }{p^{3}}}}$

ve dipol momenti:

${\displaystyle \mathbf {M} '=R^{3}\left[-{\frac {\mathbf {M} }{p^{3}}}+{\frac {2\mathbf {p} (\mathbf {p} \cdot \mathbf {M} )}{p^{5}}}\right]}$

The method of images for a sphere leads directly to the method of inversion (Jackson 1962 p35). If we have a harmonic function of position ${\displaystyle \Phi (r,\theta ,\phi )}$ where ${\displaystyle r,\theta ,\phi }$ are the spherical coordinates of the position, then the image of this harmonic function in a sphere of radius R about the origin will be Küre için görüntü yük yöntemi doğrudan evritim yöntemine yönelir (Jackson 1962 p35). Eğer elimizde ${\displaystyle \Phi (r,\theta ,\phi )}$ konumlu bir harmonik fonksiyon varsa, öyle ki${\displaystyle r,\theta ,\phi }$ küresel koordinatlar olsun, o zaman bu harmonik fonksiyonun R yarıçaplı bir kürenin merkezi etrafındaki görüntüsü:

${\displaystyle \Phi '(r,\theta ,\phi )={\frac {R}{r}}\Phi \left({\frac {R^{2}}{r}},\theta ,\phi \right)}$

Eğer potansiyel Φ ${\displaystyle (r_{i},\theta _{i},\phi _{i})\,}$ konumlarındaki, ${\displaystyle q_{i}\,}$ büyüklüğündeki yüklerden kaynaklanıyorsa, o zaman görüntü potansiyel ${\displaystyle (R^{2}/r_{i},\theta _{i},\phi _{i})\,}$ konumlarında yer alan ${\displaystyle Rq_{i}/r_{i}\,}$ yük serisinden kaynaklanır. Ayrıca eğer potansiyel Φ ${\displaystyle \rho (r,\theta ,\phi )\,}$ yük yoğunluğundan kaynaklanıyorsa, o zaman görüntü potansiyel ${\displaystyle \rho '(r,\theta ,\phi )=(R/r)^{5}\rho (R^{2}/r,\theta ,\phi )\,}$ yük yoğunluğundan kaynaklanıyor demektir.

• Kelvin transformu
• Coulomb yasası
• Diverjans teoremi
• Akı
• Gauss yüzeyi
• Schwarz yansıma prensibi
• Poisson's denklemi için teklik teoremi

• Feynman, Richard; Leighton, Robert; Sands, Matthew (1989). Feynman Lectures on Physics, Mainly Electromagnetism and Matter. Addison-Wesley. ISBN 0-201-51003-0. KB1 bakım: Birden fazla ad: yazar listesi (link)
• James Jeans (1908) The Mathematical Theory of Electricity and Magnetism, Chapter 8, Cambridge University Press.

• Purcell, Edward Mills. Berkeley Physics Course, Vol-2: Electricity and Magnetism (2nd ed.). McGraw-Hill.  An excellent introductory book that introduces the ideas of electromagnetism in a logically sound manner. Also contains beautiful diagrams.
• Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X. 
• Tikhonov, A. N. (1963). Equations of Mathematical Physics. New York: Dover Publications. ISBN 0-486-66422-8. 
• Landau, L. D. (1960). Electrodynamics of Continuous Media 2nd Edition. Londra: Elsevier. ISBN 978-0-7506-2634-7. 
• Jackson, John David (1962). Classical Electrodynamics. John Wiley & Sons, Inc.