Girih karoları

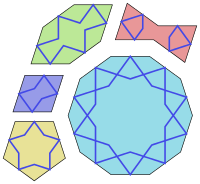
Girih karoları, İslam sanatında görülen girih desenlerini oluşturmak için kullanılan, beş tip karodur. Karoların üzerinde bulunan çizgiler, karolar belli biçimlerde döşendiğinde yıldızlar, çokgenler ve karmaşık biçimde birbirini kesen şerit desenleri meydana gelir. Bu desenlerin örnekleri binalarda, kitap kapaklarında ve halılarda görülen bir süslemedir.

Girih karolarıyla yapılan desenlerin İslam mimarisinde yaklaşık 1200 yılından beri kullanıldıkları bilinmektedir. 15. yüzyılda bunların kullanıldığı şekillerde aperiyodiklik ve özbenzeşlik gibi gelişkin matematiksel özellikler görülmekteydi.

Karolar


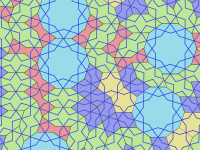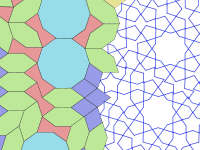Girih karolarının oluşan bir döşeme (tesselasyon).		Soldaki döşemede karolar ve girih çizgilerinin ayrı ayrı gösterilmiş hâli.

Karolarda beş şekil vardır (yukarıdaki çekle bakınız):

Düzgün bir ongen, iç açılarının her biri 144° olan.
Uzun (düzensiz konveks) bir altıgen, iç açıları 72°, 144°, 144°, 72°, 144°, 144° olan.
Bir papyon (konveks olmayan altıgen), iç açıları 72°, 72°, 216°, 72°, 72°, 216° olan.
Bir eşkenar dörtgen, iç açıları 72°, 108°, 72°, 108° olan.
Bir düzgün beşgen, iç açılarının her biri 108° olan.

Bu şekillerin her kenarı eşit uzunluktadır ve iç açıları 36° (π/5)'in katlarıdır. Beşgen olan hariç, diğerlerinin birbirine dikey iki eksen üzerinden yansıma simetrisi vardır. Bazılarında ayrıca başka simetriler de mevcuttur: ongende onlu dönel simetri (36° ile dönme), beşgende beşli dönel simetri (72° ile dönme) bulunur.

Çoğu durumda, karoların kenarları değil, meydana gelen girihler görünür, bazen çiçek benzeri küçük süsler de eklenmiş olabilir. Girihler karoların kenarlarını, kenarın tam ortasından 54° (3π/10) 'lik bir açı ile kesen çizgi parçalarıdır. Her karo kenarında, birbiriyle kesişen iki girih çizgisi bulunur. Çoğu karo içinde o karoya has, kesiksiz bir girih örüntüsü vardır ve bu örüntü karonun simetrisini takip eder. (Ancak, ongen karo için iki olasıl girih örüntüsü vardır, bunlardan birinin onlu değil, sadece beşli dönel simetrisi vardır.)

Girih döşemesinin matematiği


Yeşil Camii'de (Bursa) giriş kapısı detayı.		Soldaki desenin yukarıda gösterilen girih karolarıyla oluşturulması.

2007'de Harvard University'den Peter J. Lu ve Princeton University'den Professör Paul J. Steinhardt Science dergisinde yayımladıkları bir makalede, girih döşemelerinin, Penrose döşemeleri gibi, kristalimsi ve özbenzeş (hatta fraktal) özellikleri olduğunu gösterilmiştir.^[1]

Periyodiklik

İslam mimarisinde kullanılan çoğu girih döşemeleri periyodiktir: bir latis içinde aynı doğrultu ile tekrarlanan birim hücreleri vardır. Bazı girihlerde bulunan örüntüler ise tüm düzlemi döşeyecek şekilde tekrarlanamaz. İsfahan'da 1453'te inşa edilen Darb-ı İmam türbesindedeki desenler aperiyodiktir, yani düzenli tekrarlanmayan bir yapıya sahiptir.^[1]

Girih karolarının Penrose Karolarına dönüştürülebilir. Girih karoları Penrose Karoları yaklaşık 5 asır önce keşfedilmiştir.^[1]^[2]

Özbenzeşlik

Ancak, bazı yapılarda, büyük girih karolarını süslemek için daha küçük girih karolarından meydan gelen şekiller kullanılmıştır. Darb-ı İmam desenlerinin bir diğer özelliği farklı boyutlarda özbenzeş olmasıdır: türbeye uzaktan bakılınca görülen desenin bir benzeri, ona daha yakından bakıldığında, büyük desenin içinde yer alan detay desende yer almaktadır. Karoların daha küçük karolara bölünme işlemi, genelleştirilerek tüm düzlemin aperiyodik döşemesini sağlamaktadır.

Tarih

Günümüze kalan yapılarda görülen girih örüntülerinin analizi, ayrıca 15. yüzyıl İran belgelerinin incelemesi, bu bulguyu desteklemiştir. Ancak o dönem mimarlarının konunun matematik boyutunu ne kadar bildiklerine dair bir belirti yoktur. Girih karolarından evvel girih desenlerinin sadece bir çizgilik ve pergel ile yapıldığı bilinmektedir. Girih desenleri için girih karolarından ilk yararlandığının dair ilk kanıtlar yaklaşık 1200 yılına aittir.^[1]

1200 yılı civarında girihlerde 5- ve 10-katlı dönel simetriye sahip olan yıldız ve çokgenler belirmeye başladı. Bu şekillerin de pergel ve çizgilik ile çizilmesi mümkündür. Ancak, 15. yüzyıl civarında ongen (veya on köşeli yıldız) içeren desenlerin artık periyodik olmadığı bir düzene sahipti. Bu şekiller pergel ve çizgilikle değil, düzlemi aralarında boşluk bırkamadan kaplayabilen girih karoları ile üretiliyorlardı. Üzerinde şerit çizgileri olan bu karolar ile düzlem döşenince, şeritlerden bir girih meydana geliyordu. Ongenli girihlerin yapımında pergel ve çizgilik yerine girih karoları kullanılmasına ne zaman geçilmiş olduğu heniz kesin bilinmemektedir. Yaklaşık 1200 yılında inşa edilmiş Mama Hatun Kümbeti (Tercan, Erzincan) duvarlarındaki desenlerde ongen şekiller olmadığı için pergelli çizimin zor olacağı ama girih karosuyla yapımını gayet kolay olacağı belirtilmiştir.^[1] 1197 yılında Marage'daki Kümbed-i Kabud duvarlarındaki desenlerde şeritlerin arasındaki ince süslemenin girih karolarıyla uyumlu açılara sahip olduğu bulunmuştur.^[1] Kümbed-i Kabud'daki girih desenlerini periyodik bir yapıya sahipti, yani desenin bir kopyası belli bir mesafe kaydırılarak kendi üzerine aynen rastalatılabilecek şekilde çizilmiştir. 1200 yılında girih karolarının kullanılmakta olduğuna dair bu bulgulara rağmen, pergel-çizgilik yerine bunların kullanılmasına ilk ne zaman başlandığı kesin bilinmemektedir.^[1]^[2] Kümbeti Kabud'dan iki buçuk yüzyıl sonra (1453) İsfahan'da inşa edilen Darb-ı İmam türbesi girih desenleri çok daha karmaşık bir yapıya sahipti. Yukarıda açıklandığı üzere, Darb-ı İmam türbesi desenleri aperiyodik ve özbenzeştir.

Girih desenlerinin tasarımında girih karolarından yararlanıldığı, 15. yüzyıla ait olduğu sanılan Topkapı Parşömeninde bulunan kalıplardan görülmektedir. Bu parşömende bulunan şekillerin girih karoları imal eden zenaatkarlarca kullanılmış olabileceği öne sürülmüştür. Dolayısıyla, girih ustaları matematiğe başvurmadan ve temel ilkeleri anlamadan karmaşık döşeme şekilleri yapmış olabilirlerdi.^[3]

Kaynakça

^ ^a ^b ^c ^d ^e ^f ^g Peter J. Lu ve Paul J. Steinhardt (2007). "Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture" (PDF). Science. 315 (5815). ss. 1106-1110. Bibcode:2007Sci...315.1106L. doi:10.1126/science.1135491. PMID 17322056. 7 Ekim 2009 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 3 Ocak 2012.
^ ^a ^b "Peter J. Lu ve Paul J. Steinhardt (2007) Ek şekiller" (PDF). 26 Mart 2009 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 3 Ocak 2012.
^ Gulru Necipoglu (1995). The Topkapi Scroll: Geometry and Ornament in Islamic Architecture. Getty Research Institute.