Geometrik seri

Matematikte geometrik seri art arda gelen iki terimi arasında sabit bir oran bulunan seridir. Örneğin,

${\displaystyle {\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots }$

serisi geometriktir çünkü ilk terim dışındaki tüm terimler önceki terimi ${\displaystyle {\frac {1}{2}}\ }$'yle çarparak elde edilebilmektedir.

Seriye terimler eklendikçe toplam 1'e yaklaşmaktadır. Bu ifade, "bu serinin toplamı 1'dir" ya da "bu serinin sonsuz toplamı 1'dir" biçiminde de söylenebilmektedir.

Geometrik seriler, sonlu toplamı olan sonsuz serilere verilebilecek en basit örneklerdendir. Tarihte kalkülüsün gelişiminde büyük bir öneme sahip olan bu seriler günümüzde seri yakınsaklığı çalışmalarında kullanılmaktadır. Geometrik seriler matematiğin yanı sıra fizik, mühendislik, biyoloji, ekonomi, berimsel bilimler ve finansta da kullanılmaktadır.

Bir geometrik serinin terimleri geometrik ilerleme oluştururlar. Aşağıdaki tablo farklı ortak oranlara sahip geometrik serileri göstermektedir.

Terimlerin davranışı ortak oran r'ye bağlıdır.

r -1 ile +1 arasındaysa seri terimleri giderek küçülür ve sıfıra doğru yaklaşır. Seri, toplamı olan 1'e yakınsar.

r 1'den büyük ya da -1'den küçükse seri terimleri giderek büyür ve böylece seri herhangi bir sonlu değere yakınsamaz (seri ıraksar).

r 1'e eşitse serinin tüm terimleri 1'dir. Seri bu durumda da ıraksar.

r -1 ise seri terimleri iki değeri değişmeli olarak alır (örneğin, 2, -2, 2, -2, 2, …). Terimler iki değer arasında dalgalanır (2, 0, 2, 0, 2, … gibi). Seri bu durumda da ıraksar.

Bir geometrik serinin toplamı seri terimleri sıfıra yaklaştığı sürece sonludur. Toplam, serinin kendine benzerliği kullanılarak hesaplanabilir.

${\displaystyle s\;=\;1\,+\,{\frac {2}{3}}\,+\,{\frac {4}{9}}\,+\,{\frac {8}{27}}\,+\,\cdots }$

geometrik serisi 2/3'lük bir ortak orana sahiptir. Çarpım işlemleri bu ortak oranla yapıldığında 1 olan ilk terim 2/3'e, 2/3 olan ikinci terim 4/9'a dönüşür. İşlemler diğer terimler için de yapıldığında

${\displaystyle {\frac {2}{3}}s\;=\;{\frac {2}{3}}\,+\,{\frac {4}{9}}\,+\,{\frac {8}{27}}\,+\,{\frac {16}{81}}\,+\,\cdots }$

sonucu elde edilir. Bu seri, özgün seriyle ilk terim dışında tümüyle aynıdır. Kendine benzer herhangi bir ifadeyi hesaplamak için benzer yöntemler kullanılabilir.

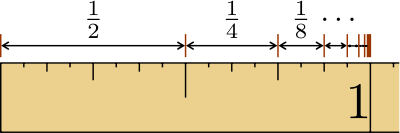
${\displaystyle r\neq 1}$ olmak koşuluyla bir geometrik serinin ilk n terimi toplamı

${\displaystyle a+ar+ar^{2}+ar^{3}+\cdots +ar^{n-1}=\sum _{k=0}^{n-1}ar^{k}=a\,{\frac {1-r^{n}}{1-r}}}$

biçiminde ifade edilebilir. Burada a, serinin ilk terimini gösterirken r, ortak oranı belirtir. Bu formül şu biçimde çıkarılabilir:

${\displaystyle {\begin{aligned}&s=1+r+r^{2}+r^{3}+\cdots +r^{n-1}\\[4pt]&rs=r+r^{2}+r^{3}+r^{4}+\cdots +r^{n}\\[4pt]&s-rs=s(1-r)=1-r^{n},{\text{ }}s={\frac {1-r^{n}}{1-r}}\end{aligned}}}$

n sonsuza giderken serinin yakınsayabilmesi için r'nin mutlak değerinin 1'den küçük olması gerekir. Toplam

${\displaystyle s\;=\;\sum _{k=0}^{\infty }ar^{k}={\frac {a}{1-r}}}$

biçimini alır. a = 1 ise bu ifade

${\displaystyle 1\,+\,r\,+\,r^{2}\,+\,r^{3}\,+\,\cdots \;=\;{\frac {1}{1-r}}}$

eşitliğine indirgenir. Bu formül şu biçimde çıkarılabilir:

${\displaystyle {\begin{aligned}&s=1+r+r^{2}+r^{3}+\cdots \\[4pt]&rs=r+r^{2}+r^{3}+r^{4}+\cdots \\[4pt]&s-rs=1,{\text{ }}s={\frac {1}{1-r}}\end{aligned}}}$

Bu formül yalnızca yakınsak seriler için (r'nin büyüklüğü 1'den küçükken) geçerlidir. Örneğin, r = 10 iken toplam tanımsızdır.

Bu akıl yürütme karmaşık düzlemde de aynı kısıtlamalarla yer alır.

Geometrik serinin yakınsadığı, geometrik ilerleme formülü kullanılarak kanıtlanabilir.

${\displaystyle {\begin{aligned}&1\,+\,r\,+\,r^{2}\,+\,r^{3}\,+\,\cdots \\[3pt]&=\;\lim _{n\rightarrow \infty }\left(1\,+\,r\,+\,r^{2}\,+\,\cdots \,+\,r^{n}\right)\\&=\;\lim _{n\rightarrow \infty }{\frac {1-r^{n+1}}{1-r}}\end{aligned}}}$

| r | < 1 için rⁿ⁺¹ → 0 olduğundan limit 1 /(1 - r) ifadesine eşit olur.

Bir yinelenen ondalık, ortak oranı 1/10'un bir üssü olan geometrik seri olarak da düşünülebilir.

${\displaystyle 0.7777\ldots \;=\;{\frac {7}{10}}\,+\,{\frac {7}{100}}\,+\,{\frac {7}{1000}}\,+\,{\frac {7}{10,000}}\,+\,\cdots }$

Geometrik seri toplam formülü, ondalığı kesre dönüştürmek amacıyla kullanılabilir.

${\displaystyle 0.7777\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {7/10}{1-1/10}}\;=\;{\frac {7}{9}}}$

Görüldüğü gibi, formül yalnızca bir ondalık için değil, art arda gelen yinelenen ondalıklar için de kullanılabilmektedir.

${\displaystyle 0.123412341234\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {1234/10000}{1-1/10000}}\;=\;{\frac {1234}{9999}}}$

Yinelenen ondalıklı herhangi bir seri şu biçimde yalınlaştırılabilir:

${\displaystyle 0.09090909\ldots \;=\;{\frac {09}{99}}\;=\;{\frac {1}{11}}}$

${\displaystyle 0.143814381438\ldots \;=\;{\frac {1438}{9999}}}$

Arşimet geometrik seri toplamını, bir parabol ve bir doğrunun çevrelediği alanı hesaplamak için kullanmıştır. Temel alınan yöntem, alanın sonsuz çoklukta üçgene ayrılması olarak tanımlanabilir.

Arşimet teoremi, parabolün altında kalan alanın mavi üçgenin alanının 4/3'üne eşit olduğunu ortaya koymaktadır. Üstün geometri bilgisini kullanan Arşimet, sarı üçgenlerin alanının mavi üçgenlerin alanının 1/8'ini, yeşil üçgenlerin alanının sarı üçgenlerin alanının 1/8'ini, ... oluşturduğunu gözlemlemiştir.

Mavi üçgenin alanı 1 olarak alınırsa toplam alan

${\displaystyle 1\,+\,2\left({\frac {1}{8}}\right)\,+\,4\left({\frac {1}{8}}\right)^{2}\,+\,8\left({\frac {1}{8}}\right)^{3}\,+\,\cdots }$

serisiyle ifade edilebilir.

İlk terim mavi üçgenin alanını, ikinci terim iki sarı üçgenin alanını, üçüncü terim dört yeşil üçgenin alanını belirtmekte ve bu seri sonsuza dek sürmektedir. Kesirler yalınlaştırıldığında

${\displaystyle 1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots }$

sonucuna ulaşılır. Bu, ortak oranı 1/4 olan bir geometrik seridir. Kesirli bölüm 1/3'e eşittir.

${\displaystyle \sum _{n=0}^{\infty }4^{-n}=1+4^{-1}+4^{-2}+4^{-3}+\cdots ={4 \over 3}\;}$

Toplam

${\displaystyle {\frac {1}{1-r}}\;=\;{\frac {1}{1-{\frac {1}{4}}}}\;=\;{\frac {4}{3}}}$ olarak hesaplanır.

Bu hesaplama, eski bir integral alma yolu olan tüketme yöntemini kullanmaktadır. Bu alan, çağdaş kalkülüste belirli integral yardımıyla bulunabilmektedir.

Fraktal çalışmalarında geometrik seriler, bir kendine benzer şeklin çevresi, alanı ve hacmini hesaplamada kullanılmaktadır.

Örneğin, Koch kar tanesinin kapladığı alan sonsuz çoklukta eşkenar üçgen olarak tanımlanabilir. Yeşil üçgenin her ayrıtı büyük mavi üçgenin ayrıt uzunluğunun 1/3'üne eşit olduğundan yeşil üçgenin alanı toplam alanın 1/9'unu kaplar. Mavi üçgenin alanı temel alındığında kar tanesinin toplam alanı

${\displaystyle 1\,+\,3\left({\frac {1}{9}}\right)\,+\,12\left({\frac {1}{9}}\right)^{2}\,+\,48\left({\frac {1}{9}}\right)^{3}\,+\,\cdots }$

olarak yazılabilir.

Bu serinin ilk terimi mavi üçgenin alanını, ikinci terimi üç yeşil üçgenin toplam alanını, üçüncü terim on iki sarı üçgenin toplam alanını göstermekte ve bu sonsuza dek sürmektedir. Baştaki 1 dışarıda tutulduğunda bu seri, ortak oranı 4/9 olan geometrik seriye dönüşmektedir. Bu geometrik serinin ilk terimi a = 3(1/9) = 1/3'tür. Böylece, alan

${\displaystyle 1\,+\,{\frac {a}{1-r}}\;=\;1\,+\,{\frac {\frac {1}{3}}{1-{\frac {4}{9}}}}\;=\;{\frac {8}{5}}}$

olarak hesaplanabilir. Koch kar tanesinin alanı temel üçgenin alanının 8/5'ine eşittir.

Bir geometrik serinin yakınsaklığının anlaşılması Zeno çatışkılarının büyük bir bölümünü saf dışı bırakmaktadır. Bunun temel nedeni, bir sonsuz kümenin toplamının | r | < 1 için sonlu kalabilmesidir. Örneğin, Zeno'nun ikiye bölme çatışkısı devinimi olanaksızlaştırmaktadır çünkü katedilecek her yol, kalan uzunluğun yarısı cinsinden ifade edilebilir. Buradaki gizli varsayım, sonlu sayıda adımın sonsuz toplamının sonlu olamayacağıdır. Bu, geometrik serilerin yakınsaklığı kavramı tarafından çürütülmüş bir önermedir.

Öklit'in Elementler adlı yapıtının IX. kitap, 35. önerme16 Kasım 2011 tarihinde Wayback Machine sitesinde arşivlendi. si geometrik serinin kısmi toplamını serinin terimleri cinsinden ifade etmektedir. Bu gösterim, çağdaş formülle birebir örtüşmektedir.

Geometrik seriler, ekonomide yıllık ödeneklerin bugünkü değerlerinin hesaplanmasında kullanılmaktadır.

Bir yıl içinde 100 lira gelir elde edecek olan birinin kazancı, parayı hemen alması durumunda elde edecek olduğu kazançtan daha azdır çünkü ele geçmeyen para yatırım aracı olarak kullanılamaz. Bir yıl sonra ele geçecek olan 100 liranın bugünkü değeri 100 / (1 + i)'dir. Burada i, yıllık faiz oranını göstermektedir.

Benzer biçimde, iki yıl sonra ele geçecek olan 100 liranın bugünkü değeri 100 / (1 + i)² olarak hesaplanır. Böylece, her yıl 100 liralık gelir elde edecek olan birinin elindeki paranın bugünkü değeri bir sonsuz seri biçiminde yazılabilir.

${\displaystyle {\frac {100}{1+i}}\,+\,{\frac {100}{(1+i)^{2}}}\,+\,{\frac {100}{(1+i)^{3}}}\,+\,{\frac {100}{(1+i)^{4}}}\,+\,\cdots }$

Bu, ortak oranı 1 / (1 + i) olan geometrik seridir. Toplam

${\displaystyle {\frac {a}{1-r}}\;=\;{\frac {100/(1+i)}{1-1/(1+i)}}\;=\;{\frac {100}{i}}}$

biçiminde yazılabilir.

Yıllık faiz oranı %10 olarak alınırsa tüm gelirin bugünkü değeri 1000 lira olur.

• Seri (matematik)
• Geometrik ilerleme
• Oran testi
• Kök testi
• Iraksak geometrik seri
• Neumann serisi
• Geometrik Artış

• Grandi serisi
• 1 + 2 + 4 + 8 + · · ·
• 1 − 2 + 4 − 8 + · · ·
• 1/2 + 1/4 + 1/8 + 1/16 + · · ·
• 1/2 − 1/4 + 1/8 − 1/16 + · · ·
• 1/4 + 1/16 + 1/64 + 1/256 + · · ·

• Eric W. Weisstein, Geometric Series (MathWorld)
• Peppard, Kim. "College Algebra Tutorial on Geometric Sequences and Series". West Texas A&M University. 7 Mayıs 2015 tarihinde kaynağından arşivlendi. 
• Casselman, Bill. "A Geometric Interpretation of the Geometric Series". 21 Aralık 2014 tarihinde kaynağından arşivlendi. 
• Michael Schreiber, "Geometric Series" 18 Şubat 2010 tarihinde Wayback Machine sitesinde arşivlendi., Wolfram Demonstrations Project, 2007