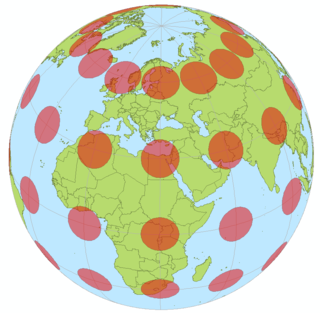
Harita projeksiyonu, 3 boyutlu yeryüzünün matematiksel transformasyon ile iki boyutlu düzlemde temsil edilmesi işlemine denir. Harita projeksiyonunun yeryüzünün şeklini nasıl değiştirdiğini anlamanın kolay bir yolu merkezinde bir ışık kaynağı bulunduğu varsayılan yeryüzünün projeksiyon yüzeyi denen bir yüzeye iz düşürülmesidir.
Yansıma, homojen bir ortam içerisinde dalgaların yansıtıcı bir yüzeye çarparak yön ve doğrultu değiştirip geldiği ortama geri dönmesi olayına denir. Yansımanın genel örnekleri ışık, ses ve su dalgalarıdır. Düzlem aynalarda yansıma, saydam ortamda hareket eden ışığın herhangi bir yüzeye çarpıp geri dönmesi olayıdır. Yansıma olayında ışığın hızı, frekansı, rengi yani hiçbir özelliği değişmez. Sadece hareket yönü değişir.
Fizikte bakışım, fizik sistemi betimleyen temel değişmezlik'lerle ilgilidir. Fiziksel sistem matematik modeller kullanılarak betimlenir ve modellerden en başarılı olanı kuram statüsüne ulaşır. Fizikte ve diğer bilimlerde modelin başarısı modelin öngörü üretebilme kapasitesiyle ve bu öngörülerin deneylerle doğrulanmasıyla ölçülür. Çoğu zaman fizik modelin değişik matematik dönüşüm'ler altında nasıl davrandığı incelenir. Eğer bir matematik dönüşüm sonucunda modelin betimlediği fizik sistem değişmiyorsa o dönüşümle ilgili bir bakışım (symmetry) olduğu söylenir. Modellerin doğrulukları deneylerden önce bu şekilde test edilir. Eğer fizik modeli daha karmaşık sistemleri betimliyorsa ya da kuantum fiziğinde olduğu gibi doğrudan gözlem yapamıyacağımız nicelikleri açıklayabilmek için geliştirilmiş ise bu karmaşık modelin içinde matematiksel olarak var olan bakışımların ortaya çıkması zaman alır ve kuramsal fizikçiler önce bu bakışımları ortaya çıkarmaya çalışırlar. Karmaşık modelin daha önce fark edilmeyen bir bakışımı bulunduğunda yeni bir korunum kanunu öngörülüyor demektir. Bazen yeni bakışımlar yeni parçacıkların varlığına işaret eder. Grup kuramı bakışımları sistematik ve matematiksel olarak inceler.
Yüzey, matematikte ve özellikle topolojide iki boyutlu çokkatlı. İki gerçel değişkenli ve gerçel değerli bir fonksiyonun üç boyutlu uzayda (R³) grafiği tipik yüzey örneğidir. Ayrıca Dünya yüzeyi, bir yumurtanın kabuğu, bir simit birer yüzeydir.

Çok katlı, topolojide soyut topolojik bir uzay. Bu uzayın her noktasının çevresi Öklit uzayına benzer. Bununla birlikte, çok katlı bir Öklit uzayı olmak zorunda değildir. Genel yapısı, bu basit yerel yapısından çok daha karmaşık olabilir. Çok katlının boyutu, yerel olarak benzediği Öklit uzayının boyutu olarak tanımlanır. Herhangi bir topolojik uzay içinse boyut kavramından söz etmek genelde olası değildir.

Topolojide ve geometride simit (torus) bir yüzeydir. Üç boyutlu uzayda bir çemberin, aynı düzlemde yatan ve çembere değmeyen bir doğru etrafında döndürülmesiyle elde edilir. Yiyecek simidin ya da yüzmek için kullanılan şişirilmiş iç lastiğin yüzeyi matematiksel olarak birer simittir.
Öklit dışı geometriler, alışılmış iç çarpım formülünden ayrı bir biçimde tanımlanmış ve reel uzayla birleşmiş iç çarpım yoluyla elde edilen geometrilerdir. Bu geometrilere Galileo ve Lorentz geometrileri örnek olarak verilebilir. Lorentz geometrisinin öne çıkan farklarından biri de iç çarpımın tanımlanmasında temel maddelerden biri olan pozitif tanımlılığı sağlamamasıdır. Öklit geometrisinde vektörler tek tür iken Lorentz geometrisinde space-like, time-like ve null-like (light-like) olmak üzere 3 tür vektör bulunmaktadır.

Matematikte karmaşık düzlem, gerçel eksen ve ona dik olan sanal eksen tarafından oluşturulmuş, karmaşık sayıların geometrik bir gösterimidir. Karmaşık sayının gerçel kısmının x-ekseni boyuncaki yer değiştirmeyle, sanal kısmının ise y-eksenindeki yer değiştirmeyle temsil edildiği değiştirilmiş bir Kartezyen düzlem olarak düşünülebilir.
Topolojide, geometrik bir nesne veya uzaya yol bağlantılıysa ve iki nokta arasındaki her yol sürekli bir şekilde bir diğerine dönüştürülebiliyorsa basit bağlantılı adı verilir.

Matematikte bir döşeme, aralarında boşluk bırakmadan veya örtüşmeden bir düzlemi kaplayan düzlemsel şekiller kümesidir. Bu kavram daha yüksek boyutlar için de genellenebilir, bu genişletilmiş anlamı için döşeme yerine tesselasyon terimi kullanılır. Tesselasyon M. C. Escher'in eserlerinde sıkça görülebilir. Tesselasyona sanat tarihi boyunca, antik mimariden modern sanata kadar rastlanabilir.
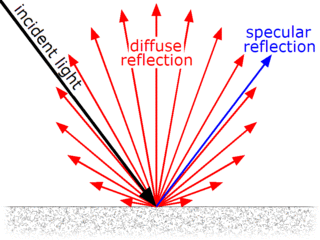
Dağınık yansıma, gelen ışığın yüzeye geldiği açıyla yansıması yerine birçok açıyla yansıması durumudur. İdeal dağınık yansıma yüzeyinde, yüzeyi çevreyen yarım küre içerisinde her doğrultuda eşit aydınlanma şiddeti görülür.

Fizik ve matematikte bir uzayın ya da nesnenin boyutu, gayriresmî olarak bu uzay ve nesne üzerindeki herhangi bir noktayı belirlemek için gereken minimum koordinat sayısı olarak tanımlanır. Bir doğru üzerindeki bir noktayı tanımlamak için bir koordinat gerektiğinden doğrunun bir boyutu vardır. Düzlem, kare ya da daire yüzeyinin iki boyutu vardır, çünkü bu yüzeyler üzerindeki herhangi bir noktayı tanımlamak için iki koordinata ihtiyaç vardır. Yine aynı şekilde küre, silindir ya da küpün içindeki bir noktayı tanımlamak için üç koordinat gerektiğinden bu boşluk üç boyutludur. İzafiyet Teorisi'nde ise zaman, dördüncü ve uzaysal olmayan boyut olarak eklenir.

Yöney alan, Öklid uzayının seçilen bir alt kümesinin her bir noktasında yöneyin belirlenmesidir. Düzlemdeki bir yöney alanı, her biri düzlemdeki bir noktaya ilişik, yönü ve büyüklüğü olan oklar topluluğu olarak düşünülebilir.

Diferansiyel geometrinin matematiksel alanı içinde, Levi-Civita paralelkenarımsı bir eğri uzay içinde bir dörtlüyanal Öklidyen düzlem içinde onun bir paralelkenar genelleme inşasıdır. Bu isim araştırmacı Tullio Levi-Civitaya ithafendir. Bir paralelkenar gibi, bir paralelkenarımsının iki zıt yüzleri AA′ ve BB′ paralel düz olmasına rağmen, ancak dördüncü kenar A′B′ değil, genel olarak, paralel ya da AB kenarı boyunca aynı uzunlukta olacaktır.
Bu diferansiyel geometri konuların bir listesidir. Ve aynı zamanda Lie grubu konularının listesi metrik geometri ve diferansiyelin sözlüğü bkz.
Matematikte açık birim disk, P noktasına uzaklığı 1'den küçük noktalar kümesidir.

Uzay, nesnelerin ve olayların göreceli konuma ve yöne sahip olduğu sınırsız üç boyutlu bir boyuttur. Modern fizikçiler genellikle zamanla, uzay-zaman olarak bilinen sınırsız dört boyutlu bir sürekliliğin parçası olduğunu düşünmesine rağmen, fiziksel alan genellikle üç doğrusal boyutta düşünülür. Mekan kavramının fiziksel evrenin anlaşılması için temel öneme sahip olduğu düşünülmektedir. Bununla birlikte, filozoflar arasında kendisinin bir varlık mı, varlıklar arasındaki ilişkinin mi yoksa kavramsal çerçevenin bir parçası mı olduğu konusunda anlaşmazlık devam eder.
Perseus, Pergeli Apollonius tarafından incelenen konik kesitlere benzer şekilde spiral kesitler kavramını icat eden eski bir Yunan geometrici.

Matematikte Riemann yüzeyi, özellikle karmaşık analizde bahsi geçen tek boyutlu karmaşık bir manifolddur. Bu yüzey(ler) ilk olarak Bernhard Riemann tarafından incelenmiş ve isimlendirilmiş. Riemann yüzeyleri, karmaşık düzlemin deforme olmuş versiyonları olarak düşünülebilir: her noktanın yakınında karmaşık düzlemin yerel olarak yamaları gibi görünürler, ama topolojisi oldukça farklı olabilmektedir.

Calabi–Yau Manifoldu veya Calabi–Yau space, cebirsel geometride, Ricci düzlüğü gibi özelliklere sahip olan ve teorik fizikte uygulamalara olanak sağlayan özel bir manifold türüdür. Özellikle süper sicim teorisinde, uzay-zamanın ekstra boyutlarının bazen 6 boyutlu Calabi–Yau manifoldu formunu alacağı varsayılır ve bu da ayna simetrisi fikrine yol açmaktadır. Manifoldun ismi, bu tür yüzeylerin var olabileceğini ilk tahmin eden Eugenio Calabi'den ve Calabi varsayımını kanıtlayan Shing-Tung Yau'dan (1978) sonra 1985 yılında Candelas ve arkadaşları tarafından icat edilmiştir.










