Gabriel Lamé

Gabriel Lamé
Doğum	22 Temmuz 1795(1795-07-22) Tours, Fransa
Ölüm	1 Mayıs 1870 (74 yaşında) Paris, Fransa
Defin yeri	Montparnasse Mezarlığı 48°50′17″K 2°19′37″D / 48.83806°K 2.32694°D / 48.83806; 2.32694
Milliyet	Fransız
Vatandaşlık	Fransa
Eğitim	Ecole Polytechnique, Mines ParisTech, Lycée Louis-le-Grand
Tanınma nedeni	Lamé eğrisi Lamé fonksiyonu Lamé parametreleri Lamé'nin özel kuartiki
Ödüller	Officer of the Legion of Honour
Kariyeri
Dalı	Matematik, Fizik, Mekanik, Mühendislik
Çalıştığı kurum	Ecole Polytechnique, Paris Üniversitesi

Gabriel Lamé (22 Temmuz 1795 - 1 Mayıs 1870), eğrisel koordinatları kullanarak kısmi diferansiyel denklemler teorisine ve (doğrusal elastikiyet ve sonlu gerilme teorisinin matematiksel soyutlamaları detaylandırdığı) matematiksel elastikiyet teorisine katkıda bulunan bir Fransız matematikçiydi.

Lamé, Tours'da, bugünkü Indre-et-Loire bölümünde (département) doğdu.

Gabriel Lamé, École Polytechnique'de bir öğrenciydi, 1813'te girdi ve 1817'de mezun oldu. Daha bu lisans yıllarında Lamé araştırma makaleleri yazıyordu ve Mémoire sur les intersections des lignes et des surfaces adlı ilk makalesi Gergonne's Journal'da 1816-17'de yayınlandı. Lamé, École Polytechnique'den mezun olduktan sonra, Paris'teki École des Mines'de mühendislik okudu ve 1820'de oradan mezun oldu. Lamé, Ecole des Mines'deyken bu sefer kristallerin yüzleri arasındaki açıları hesaplamak için icat ettiği bir yöntemle ilgili ikinci çalışmasını yayımladı.

1820'de Lame, meslektaşı Émile Clapeyron ile birlikte Rusya'ya gitti. İlk bakışta iki genç matematikçi için oldukça tuhaf bir kariyer hamlesi gibi görünen bu olayın arka planına biraz bakmak gerekir. Alexander I, 1801'den 1825'e kadar Rusya'nın imparatoruydu. Fransız Devrimi ve onu takip eden Fransa'daki olaylar, Alexander'a bilimsel bilginin ve onun askeri teknikler ve endüstriyel gelişmedeki uygulamalarının önemini göstermişti. Rusya'nın güçlü olması için aynı şeyi yapması gerektiğini anladı. Avrupa ve Avrupalı bilim insanlarına baktı ve onları Rus bilim insanlarıyla işbirliği yapmaya teşvik edecek politikalar getirmeye çalıştı. Öğretmenleri en son bilimsel teorileri öğretmek ve Rusya ile Avrupa arasında bilimsel bağlantılar kurmak için Rusya'ya gelmeye teşvik etti. Bu politika doğrultusunda, Rus hükûmeti Fransa'ya bir talepte bulundu ve Fransa'ya Lamé ve Clapeyron'u St Petersburg'a göndererek yanıt verdi.

Lamé, St Petersburg'daki Institut et Corps du Genie des Voies de Communication'da profesör ve mühendis olarak atandı. İlk başta Lame için işler oldukça zordu, ancak daha sonra ziyareti oldukça verimli oldu. Analiz, fizik, mekanik, kimya ve mühendislik konularında dersler verdi. Orada geçirdiği 12 yıl boyunca, bazıları Clapeyron ile ortak olmak üzere hem Rus hem de Fransız dergilerinde makaleler yayınladı. Örneğin, Journal des voies de communications, Journal du genie civil, Bulletin des sciences mathématiques, Receuil des savants etrangers ve 1826'da yayımlanmaya başladıktan sonra Journal für die reine und angewandte Mathematik (Crelle's Journal)'da yayınlar yaptılar.

Lame'nin St Petersburg'daki zamanında meydana gelen ilginç bir olay anlatılmaktadır.^[1] Lame'nin Cauchy'nin yeni kesin analiz fikirlerini yayma girişimiyle ilgilidir. Lamé'nin ders verdiği Enstitü'de bir profesör, Taylor teoreminin kanıtını içeren bir kitap yazmıştı. Lamé, Cauchy'nin argümanlarını kullanarak kanıtı eleştiren bir el yazısı hazırladı. Lame'nin St Petersburg'daki çalışmasının bir diğer yanı, şehrin çevresinde köprüler ve yollar inşa etmek için hazırlanan planlara yardım etmesiydi. Bu sırada, demiryolu gelişiminin muazzam potansiyelinin daha fazla farkına vardı ve bu, Fransa'ya döndükten sonra onun için büyük bir ilgi konusu olacaktı. Bundan önce, Liverpool-Manchester hattı 15 Eylül 1830'da İngiltere'de açıldığında oradaydı.

Bradley,^[2] Lamé'nin Rusya'daki zamanı hakkında çok daha fazla ayrıntı veriyor. Makalesinde şu sonuca varıyor:

1832'de Lamé Paris'e döndü ve ilk başta Clapeyron ve diğer iki kişiyle ortaklaşa kurulan bir mühendislik firmasının parçasını oluşturdu. Sadece birkaç ay sonra ve hala 1832'de Lamé, Ecole Polytechnique'de fizik başkanlığını kabul etti. Bununla birlikte, ilgi alanlarını öğretim ve araştırmayla sınırlamadı, çünkü o alanda danışmanlık yapmaya hazır bir mühendis olarak kaldı. 1836'da maden baş mühendisi olarak atandı ve aynı zamanda Paris'ten Versailles'e demiryolunun ve 1837'de açılan Paris'ten St Germain'e demiryolunun inşasında yer aldı.

Lame, Louis Puissant'ın geometri bölümünde bir boşluk bırakarak öldüğü 1843'te Académie des Sciences'a seçildi. Ertesi yıl École Polytechnique'deki fizik kürsüsünden ayrıldı ve Sorbonne'da matematiksel fizik ve olasılık alanında bir görevi kabul etti. 1851'de Sorbonne'da matematiksel fizik ve olasılık kürsüsüne atandı.

Çok çeşitli konularda çalıştı. Genellikle üstlendiği mühendislik görevlerindeki problemler onu matematiksel soruları incelemeye yöneltti. Örneğin, tonozların stabilitesi ve asma köprülerin tasarımı konusundaki çalışmaları, onu elastisite teorisi üzerinde çalışmaya yönlendirdi. Aslında bu geçici bir ilgi değildi, çünkü Lamé bu konuya önemli katkılarda bulundu. Başka bir örnek, onu genel eğrisel koordinatlar teorisine götüren ısının iletimi üzerine yaptığı çalışmadır.

Eğrisel koordinatlar, Lamé'nin elinde çok güçlü bir araç olduğunu kanıtladı. Bunları Laplace denklemini elipsoidal koordinatlara dönüştürmek ve böylece değişkenleri ayırmak ve elde edilen denklemi çözmek için kullandı. Lame fonksiyonları, elipsoidal harmonik teorisinin bir parçasıdır. Lamé'nin kariyerinin alameti farikası, bir konudan diğerine oldukça mantıklı bir şekilde geçmekti, ancak çoğu zaman, orijinalinden çok uzak problemler üzerinde çalışıyordu. Bu, aşağıdaki denklemi incelemeye yönlendirildiği için eğrisel koordinatlarla oldu:

${\displaystyle ({\frac {x}{a}})^{n}+({\frac {y}{b}})^{n}+({\frac {z}{c}})^{n}=0}$

bunu, homojen olmayan biçimde aşağıdaki şekilde yazdı:

${\displaystyle ({\frac {x}{a}})^{n}+({\frac {y}{b}})^{n}=1}$

burada ${\displaystyle a=b}$ ile eşitlik ${\displaystyle x^{n}+y^{n}=a^{n}}$ yani Fermat'nın son teoremine yönlendirildi. Temelde uygulamalı bir matematikçi olmasına rağmen, Lamé, n = 7 özel durumunu çözerek probleme önemli bir katkı yaptı. Aslında tüm problemi bir aşamada çözdüğüne inanıyordu, ancak karmaşık sayıların belirli alt halkalarında benzersiz çarpanlara ayırma eksikliğini gözden kaçırmıştı ve kanıtı kusurluydu.

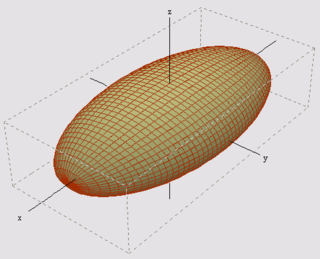
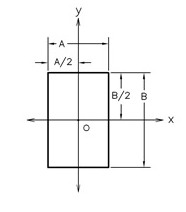
Lamé'nin genel eğrisel koordinatlar teorisi ve şu anda Lamé eğrileri veya süper elipsler olarak bilinen ve aşağıdaki denklemle tanımlanan elips benzeri eğri sınıflarının notasyonu ve çalışmasıyla tanındığını söylemek yanlış olmayacaktır:

${\displaystyle \left|\,{x \over a}\,\right|^{n}+\left|\,{y \over b}\,\right|^{n}=1}$

burada n herhangi bir pozitif gerçel sayıdır.

Ayrıca diferansiyel geometri üzerinde önemli çalışmalar yaptı ve sayı teorisine bir başka katkı olarak, Öklid algoritmasındaki bölüm sayısının asla küçük sayıdaki basamak sayısının beş katını geçmediğini gösterdi. Yani hesaplama karmaşıklığı teorisinin başlangıcını işaret eden Öklid algoritmasının çalışma süresi (zaman karmaşıklığı) analizi ile tanınır. Fibonacci sayılarını kullanarak, a ve b tam sayılarının en büyük ortak bölenini bulurken, algoritmanın en fazla 5k adımda çalıştığını kanıtladı; burada k, b'nin (ondalık) basamak sayısıdır.

Yukarıda belirttiğimiz gibi, iki elastik sabitin kendi adını verdiği mühendislik matematiği ve elastikiyet üzerinde çalıştı. Kristal malzemede difüzyonu inceledi.

Lamé, birçokları tarafından, zamanının önde gelen Fransız matematikçisi olarak kabul edildi, özellikle de hiçbir zaman kolayca övülmeyen Gauss bu görüşe sahipti. Fransızlar onun bir matematikçi için fazla pratik, bir mühendis içinse fazla teorik olduğunu düşünüyor gibiydiler. Kendi görüşü, eğrisel koordinatların onun en önemli katkısı olduğuydu, ancak matematik tarihinde garip bükülmeler ve dönüşler var ve Lamé, bunları tanıttıktan çok kısa bir süre sonra eğrisel koordinatlar, Hermite, Klein ve Bôcher tarafından ortaya konan genellemeler yoluyla modası geçmiş oldu.

Mühendisliğe en önemli katkılarından birisi de bir mahfazadaki dübel piminde görülene benzer bir presli geçme bağlantısının gerilimlerini ve yeteneklerini / kapasitelerini doğru bir şekilde tanımlamaktı.

1854'te İsveç Kraliyet Bilimler Akademisi'ne yabancı üye seçildi.

Lame 1870'te Paris'te öldü.

• 1818: Examen des différentes méthodes employées pour résoudre les problèmes de géométrie (Vve Courcier); Alternatif bağlantı
• 1840: Cours de physique de l'Ecole Polytechnique. Tome premier, Propriétés générales des corps—Théorie physique de la chaleur (Bachelier)
• 1840: Cours de physique de l'Ecole Polytechnique. Tome deuxième, Acoustique—Théorie physique de la lumière (Bachelier)
• 1840: Cours de physique de l'Ecole Polytechnique. Tome troisième, Electricité-Magnétisme-Courants électriques-Radiations (Bachelier)
• 1852: Leçons sur la théorie mathématique de l'élasticité des corps solides 12 Ağustos 2021 tarihinde Wayback Machine sitesinde arşivlendi. (Bachelier)
• 1857: Leçons sur les fonctions inverses des transcendantes et les surfaces isothermes (Mallet-Bachelier)
• 1859: Leçons sur les coordonnées curvilignes et leurs diverses applications (Mallet-Bachelier)
• 1861: Leçons sur la théorie analytique de la chaleur (Mallet-Bachelier)

• Adı Eyfel Kulesi'ne yazılan 72 isimden biridir.
• Aydaki bir kratere onun adı verilmiştir.^[3]

• S. L. Greitzer, "Lamé, Gabriel", Biography in Dictionary of Scientific Biography (1970-1990), New York, 14 Şubat 2021 tarihinde kaynağından arşivlendi, erişim tarihi: 12 Ağustos 2021 
• M. M. Voronina (1987), Gabriel Lame, 1795-1870, Leningrad: 'Nauka', 12 Ağustos 2021 tarihinde kaynağından arşivlendi, erişim tarihi: 12 Ağustos 2021 
• J. Bertrand, C. Combes & V. Puiseau (1870), "Mélanges. Funérailles de M. Lamé, le Mardi 3 Mai 1870" (PDF), Bulletin des Sciences Mathématiques et Astronomiques I, ss. 189-195, 224-228, 12 Ağustos 2021 tarihinde kaynağından arşivlendi (PDF), erişim tarihi: 12 Ağustos 2021 
• O. I. Franksen & I. Grattan-Guinness (1989), "The earliest contribution to location theory? Spatio-economic equilibrium with Lamé and Clapeyron, 1829", Math. Comput. Simulation, 31 (3), ss. 195-220, doi:10.1016/0378-4754(89)90159-6 
• Ju M. Gaiduk & I. A. Naumov (1965), "Russian pages of G. Lamé's biography", Istoriko-Matematicheskie Issledovaniya (Rusça), cilt 16, ss. 337-372 

• Lamé krateri
• Piet Hein
• Lamé'nin özel kuartiki
• Julius Plücker
• Stefan problemi
• Süper elips
• Lamé parametreleri

• Eric W. Weisstein, Süperelips (MathWorld)
• "Lame'nin Oval / Süper Elips (Java uygulaması)". 27 Şubat 2009 tarihinde kaynağından arşivlendi. 
• O'Connor, John J.; Robertson, Edmund F., "Gabriel Lamé", MacTutor Matematik Tarihi arşivi