Göreceli olasılıklar oranı

Göreceli olasılıklar oranı veya tahmini rölatif risk veya, yaygınca kullanılan İngilizce karşılığıyla "odds ratio", etki büyüklüğünün bir ölçüsüdür, Bayes istatistiğinde ve lojistik regresyonda özellikle önemlidir.^[1]

Bir olayın bir grup için olasılıklar oranının başka bir grup için olasılıklar oranına olan oranıdır; veya bunun bir örnekleme dayalı bir tahminidir. Bu iki grup örneğin, erkek ve kadın grupları, deneysel ve kontrol grupları veya herhangi başka iki bölümlü bir sınıflama olabilir. Bu gruplar için bir olayın olasılığı p (birinci grup) ve q (ikinci grup) ise, göreceli olasılıklar oranı:

{p/(1-p) \over q/(1-q)}={\frac {\;p(1-q)\;}{\;q(1-p)\;}}.

Göreceli olasılıklara oranının 1 olması, söz konusu olayın veya durumun her iki grup için de aynı derecede olası olduğu anlamına gelir. Bu oran 1'den büyükse olay veya durum birinci grup için daha olası demektir. Göreceli olasılık oranı sıfırdan küçük olamaz. Birinci grubun olasılık oranı sıfıra yaklaştıkça göreceli olasılık oranı sıfıra yaklaşır; ikinci rubun olasılıklar oranı sıfıra yaklaştıkça, göreceli olasılık oranı artı sonsuza ıraksar.

Örneğin, 100 erkekten oluşan bir örnekte, 90 tanesi geçen hafta sigara içmiş, 100 kadından oluşan bir örnekte ise aynı süre zarfında 20'si sigara içmiş olsun. Bir erkeğin sigara içmesinin olasılık oranı 90'a 10, yani 9:1'dir, kadınlar için ise olasılık oranı 20'ye 80 veya 1:4 = 0,25:1'dir. Göreceli olasılık oranı dolayısıyla 9/0,25, yani 36'dır. Bu rakam erkeklerin kadınlardan çok daha sigara içme olasılığına sahip olduğunu ifade eder. Yukarıda verilen formülü kullanarak da aynı sonuç elde edilir:

{0.9/0.1 \over 0.2/0.8}={\frac {\;0.9\times 0.8\;}{\;0.1\times 0.2\;}}={0.72 \over 0.02}=36.

Yukarıdaki örnek, göreceli olasılıklar oranının belli konumlara olan duyarlılığını gösterir: bu örnekte erkekler kadınlara göre 90/20=4,5 kat daha fazla sigara içmektedirler ama sigara içme olasılıklar oranı 36 katıdır. Göreceli olasılık oranının logaritması, yani olasılıkların logit değerlerinin farkı, bu etkiyi yumuşatır ve grupların sıralamasına göre simetrik olmasını sağlar. Örneğin doğal logaritma kullanınca 36 değerinde bir göreceli olasılıklar oranı 3.584'e karşılık gelir, 1/36'lık bir oran ise -3.584'e.

Tibbi ve sosyal bilimlerde lojistik regresyonun gittikçe yaygınlaşan kullanımı yüzünden göreceli olasılık oranı klinik denemeler, anket çalışmaları ve epidemiyolojide (vaka-kontrol çalışmaları gibi) sonuçların sunulmasında sıkça kullanılır olmuştur. Raporlarda çoğu zaman "OR" ("odds ratio") olarak kısaltılır.

Ayrıca bakınız

Tehlike oranı

Dış bağlantılar

Göreceli olasılık oranı hesaplayıcısı (İngilizce)

Kaynakça

^ Kault, David. (2003). Statistics with common sense. Westport, Conn.: Greenwood Press. ss. 183-186. ISBN 0-313-32209-0. OCLC 50004032.

İlgili Araştırma Makaleleri

Sigara, kıyılmış tütünün kağıda sarılmasıyla üretilen, yakılıp dumanı çekilerek tüketilen bir nesnedir. Tütündeki psikotrop madde olan nikotin, sigarayı oldukça bağımlılık yapıcı kılar. Günümüzde çok yaygın olarak kullanılan bu ürünün, 18. yüzyılda Avrupa'ya İspanyol denizciler tarafından Amerika'dan getirildiği düşünülmektedir. Sigara, sigara tabakası veya sigara paketi içinde tutulur.

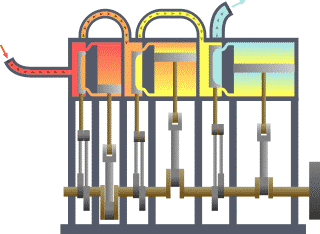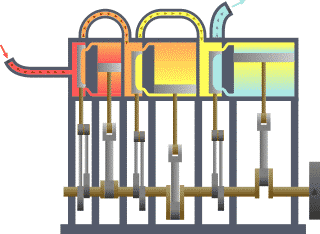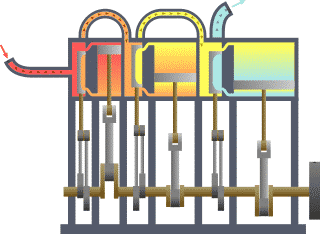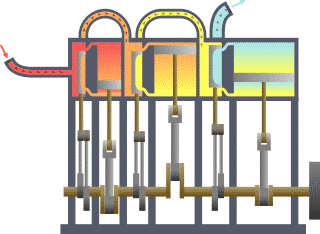
<span class="mw-page-title-main">Termodinamik</span> enerji bilimi

Termodinamik; ısı, iş, sıcaklık ve enerji arasındaki ilişki ile ilgilenen bilim dalıdır. Basit bir ifadeyle termodinamik, enerjinin bir yerden başka bir yere ve bir biçimden başka bir biçime transferi ile ilgilenir. Bu süreçteki anahtar kavram, ısının, belirli bir mekanik işe denk gelen bir enerji biçimi olmasıdır.

<span class="mw-page-title-main">Rasyonel sayılar</span>

Rasyonel sayılar, iki tam sayı arasındaki oranı temsil eden, bir pay $p$ ve sıfırdan farklı bir payda $q$ olmak üzere, bir bölme işlemi veya kesir formunda ifade edilebilen sayıları tanımlar. Örneğin, $\text{[math]}$ rasyonel bir sayı olarak kabul edilir, bu kapsamda her tam sayı da rasyonel sayılar kategorisindedir. Rasyonel sayılar kümesi, çoğunlukla kalın harf biçimindeki Q veya karatahta vurgusu kullanılarak $\text{[math]}$ şeklinde ifade edilir.

Matematikte, bir polinom belirli sayıda bağımsız değişken ve sabit sayıdan oluşan bir ifadedir. Polinom kendi içinde toplama, çıkarma, çarpma ve negatif olmayan sayının üssünü alma işlemlerini kullanır. Örnek olarak tek bilinmeyenli bir polinom olan $x 2 - 4 x + 7$ , ikinci dereceden oluşan bir polinomdur. Diğer bir örnek olarak, $x 2 - 4/ x + 7 x 3/2$ bir polinom değildir, çünkü polinomlarda terimlerin derecelerinin doğal sayı olma zorunluluğu vardır 2. terimde $x$ ′i ele alan bir bölme işlemi $x$ 'in derecesini negatif yapmaktadır ve 3. terim doğal sayı olmayan bir derece içermektedir (3/2).

Regresyon analizi, iki ya da daha çok nicel değişken arasındaki ilişkiyi ölçmek için kullanılan analiz metodudur. Eğer tek bir değişken kullanılarak analiz yapılıyorsa buna tek değişkenli regresyon, birden çok değişken kullanılıyorsa çok değişkenli regresyon analizi olarak isimlendirilir. Regresyon analizi ile değişkenler arasındaki ilişkinin varlığı, eğer ilişki var ise bunun gücü hakkında bilgi edinilebilir. Regresyon terimi için öz Türkçe olarak bağlanım sözcüğü kullanılması teklif edilmiş ise de Türk ekonometriciler arasında bu kullanım yaygın değildir.

Bir resmin çerçeve oranı eni ve boyu arasındaki oransal ilişkiyi tarif eder.

<span class="mw-page-title-main">Bölme</span> Matematik işlemi

Bölme, aritmetiğin temelini oluşturan dört ana işlemden biri olarak kabul edilir. Diğer üç ana işlem ise toplama, çıkarma ve çarpma olarak sıralanır. İşlem sırasında bölünen miktar bölünen olarak adlandırılırken, bu miktarın bölündüğü sayıya bölen denir ve işlemin sonucunda elde edilen değer bölüm olarak tanımlanır.

Poisson dağılımı, olasılık kuramı ve istatistik bilim kollarında bir ayrık olasılık dağılımı olup belli bir sabit zaman birim aralığında meydana gelme sayısının olasılığını ifade eder. Bu zaman aralığında ortalama olay meydana gelme sayısının bilindiği ve herhangi bir olayla onu hemen takip eden olay arasındaki zaman farkının, önceki zaman farklarından bağımsız oluştuğu kabul edilir.

Olasılık kuramı ve istatistik bilim dallarında geometrik dağılım şu iki şekilde ifade edilebilen ayrık olasılık dağılımıdır:

Bütün tam sayılar setine, yani { 1, 2, 3, .... } üzerine, bağlı olarak X sayıda Bernoulli denemesinde ilk başarıyı elde etmenin olasılık dağılımı; veya
Bütün tam sayılar setine, yani {1, 2,3, ....} üzerine, bağlı olarak ilk başarıyı elde etmeden Y = X − 1 başarısızlık sayısı olasılık dağılımı.

Bayes teoremi, olasılık kuramı içinde incelenen önemli bir konudur. Bu teorem bir rassal değişken için olasılık dağılımı içinde koşullu olasılıklar ile marjinal olasılıklar arasındaki ilişkiyi gösterir. Bu şekli ile Bayes teoremi bütün istatistikçiler için kabul edilir bir ilişkiyi açıklar. Bu kavram için Bayes kuralı veya Bayes savı veya Bayes kanunu adları da kullanılır.

Betimsel istatistikte çeyrekler açıklığı sıralanmış bir veri dizisinin orta yarısını (%50'sini) kapsayan ve üçüncü dörtte birlik ve birinci dörtte birlik aralığını veya farkını gösteren bir istatistiksel yayılma ölçüsüdür. Birinci dörtte birlik sıralanmış veri dizisinin ilk %25'inden büyük ve üçüncü dörtte birlik sıralanmış veri dizisinin %25'inden daha küçük olduğu için, bu iki dörtte birlik arasında kalan veri yüzdesi %50'dir. Çeyrekler açıklığı ölçüm birimi veri ölçüm birimi ile aynıdır. İngilizcesi IQR'dir.

Genetik bağlantı, belli genetik konumların (lokusların) veya gen alellerin beraberce kalıt olmaları durumdur. Aynı kromozom üzerindeki genetik lokuslar birbirine fiziksel olarak bağlıdırlar, bu yüzden mayoz bölünmede alellerin ayrışması sırasında, bunlar beraber kalma eğiliminde oldukları için bağlantılı oldukları söylenir. Farklı kromozomlardaki gen alelleri bağlantılı değillerdir, mayoz sırasında kromozomların bağımsız tertiplenmelerinden dolayı.

Olasılık teorisinde ve istatistikte bir olayın lehine olan olasılıklar oranı, p / 'dir, burada p bu olayın olasılığıdır. Bu olayın aleyhine olan olasılıklar oranı da (1 − p) / p 'dir.

Göreceli risk veya rölatif risk, bir risk etkenine sahip olanların, olmayanlara göre hastalık geliştirme oranıdır. Göreceli risk, maruz kalan grup ile maruz kalmayan grubun bir olayı geliştirme ihtimalinin oranı alınarak hesaplanır.

\text{[math]}

Sağkalım analizi, biyolojik organizmalarda ölüm ve mekanik sistemlerde başarısızlık ile ilgilenen bir istatistik dalıdır. Bu konu mühendislikte güvenilirlik teorisi veya güvenilirlik analizi, iktisat ve sosyolojide ise süre analizi veya süre modellemesi olarak adlandırılır.

Kesir, bir birimin bölündüğü parçalardan birinin veya birkaçının bütüne oranını ifade eden sayı. Kesir kavramı, ondalık sayılardan ve yüzdelerden ayırmak amacıyla sıklıkla sadece "bayağı kesirleri" tanımlamak için kullanılır.

Epidemiyoloji risk faktörü sağlık ve enfeksiyonun yüksek riskli hastalık /enfeksiyonla birleştirildiğinde değişkendir. Bazen belirleyicide kullanılabilir. Yüksek veya düşük riskle birleştirildiğinde değişken olabilmektedir.

Matematiksel istatistik, istatistiksel veri toplama tekniklerinin aksine, matematiğin bir dalı olan olasılık teorisinin istatistiğe uygulanmasıdır. Bunun için kullanılan özel matematiksel teknikler arasında matematiksel analiz, doğrusal cebir, stokastik analiz, diferansiyel denklemler ve ölçü teorisi bulunur.

Temsil kısayolu veya buluşsal yöntemi, belirsizlik altındaki bir olayın olasılığı hakkında yargılarda bulunurken kullanılır. Psikologlar Amos Tversky ve Daniel Kahneman tarafından 1970'lerin başında "[bir olayın] (i) temel özellikleri bakımından ana popülasyona benzer olma ve (ii) üretildiği sürecin göze çarpan özelliklerini yansıtma derecesi" olarak önerilen bir grup buluşsal yöntemden biridir. Buluşsal yöntemler, "genellikle bizi gitmemiz gereken yere - ve hızlı bir şekilde - götüren, ancak bazen bizi rotadan çıkarma pahası olan yargısal kısayollar" olarak tanımlanır. Buluşsal yöntemler kullanışlıdırlar çünkü karar vermede çabayı azaltmadan ve basitleştirmeden yararlanırlar.

Yineleme aralığı veya tekrar aralığı; depremler, seller, heyelanlar veya nehir deşarjları gibi olayların meydana gelmesi arasındaki ortalama süre veya tahmini ortalama süredir.

Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.