
Ockham'ın usturası, Occam'ın usturası, Ocham'ın usturası, tutumluluk yasası veya basitlik yasası, "olasılıkların zorunluluk olmadan çoğaltılmaması gerektiği" problem çözme ilkesi. Fikir, ilahi mucizeler fikrini savunmak için basitliği tercih eden skolastik filozof ve teolog, İngiliz Fransisken rahibi Ockhamlı William'a atfedilir. "En basit açıklama büyük olasılıkla doğru olandır" gibi ifadelerle çeşitli şekillerde yorumlanmıştır. Bu felsefi ustura, aynı tahminle ilgili rakip hipotezler sunulduğunda, en az varsayıma sahip çözümün seçilmesi gerektiğini savunur. Dolayısıyla, farklı tahminler yapan hipotezler arasında seçim yapmanın bir yolu değildir.

Bir asal sayı, yalnızca 1'den büyük olup kendisinden küçük iki doğal sayının çarpımı olarak ifade edilemeyen bir doğal sayıdır. 1'den büyük ve asal olmayan doğal sayılara bileşik sayı adı verilir. Örneğin, 5 bir asal sayıdır çünkü onu bir çarpım olarak ifade etmenin mümkün olan yolları, 1 × 5 veya 5 × 1, yalnızca 5 sayısını içermektedir. Ancak, 4 bir bileşik sayıdır çünkü bu, her iki sayının da 4'ten küçük olduğu bir çarpım şeklindedir. Asal sayılar, aritmetiğin temel teoreminden ötürü sayı teorisi alanında merkezi öneme sahiptir: 1'den büyük her doğal sayı, ya bir asal sayıdır ya da asal sayıların çarpımı olarak, sıralamalarından bağımsız bir şekilde, benzersiz olarak çarpanlarına ayrılabilir.

Fibonacci, ayrıca Leonardo Bonacci, Pisalı Leonardo veya Leonardo Bigollo Pisano olarak da bilinen Pisa Cumhuriyetinden İtalyan matematikçi, "Orta Çağ'ın en yetenekli Batılı matematikçisi" olarak kabul edilir.

I. İsaakios Komninos, 1057-1059 yılları arasında tahtta kalan Bizans imparatoru.

Godfrey Harold Hardy, sayı teorisi ve matematiksel analizdeki başarılarıyla tanınan İngiliz bir matematikçiydi. Biyolojide, popülasyon genetiğinin temel bir ilkesi olan Hardy-Weinberg ilkesi olarak da bilinen, tür içi gen alışverişinin fazla olduğu topluluklarda başat ve çekinik genetik özelliklerin dağılımının oranı hakkındaki teorisiyle bu konudaki tartışmaya son vermiştir.
Matematikte Christoffel–Darboux teoremi Elwin Bruno Christoffel (1858) ve Jean Gaston Darboux (1878) tarafından tanıtılmış, ortogonal polinomlar için bir özdeşliktir.
Doğu Roma iç savaşı (1341-1347) Doğu Roma İmparatorluğu'nun Balkan topraklarında, III. Andronikos'un ölümünden sonra ortaya çıkıp 6 yıl süren iç savaş dönemidir. Bazen İkinci Paleologos İç Savaşı olarak da geçer. Bu iç savaş, Doğu Roma cemiyeti içinde aristokrasi ile orta ve alt sınıf arasında gelişmiş, sınıflar arası mücadele yaratmıştır. Aristokrasi tarafında VI. İoannis, orta ve alt sınıf tarafında mevcut hanedan mensupları yer almıştır.
Drungarios, Geç Roma ve Bizans dönemlerinde drungos olarak bilinen yapının komutanına verilen rütbe.

Alan Baker, sayı teorisindeki etkili yöntemler, özellikle de transandantal sayı teorisinden doğan konular üzerine yaptığı çalışmalarla tanınan İngiliz bir matematikçiydi.

Matematikte graf ya da çizge, nesne çiftlerinin bir anlamda "ilişkili" olduğu bir dizi nesne kümesini belirleyen bir yapıdır. Nesneler, köşeler adı verilen matematiksel soyutlamalara karşılık gelir ve ilgili düğüm çiftlerinin her birine bir kenar, ayrıt adı verilir. Tipik olarak bir graf, kenarları için çizgiler veya eğriler ile birleştirilen, düğümler için bir nokta veya daire kümesi olarak diyagram şeklinde gösterilir. Graflar ayrık matematikte çalışmanın amaçlarından biridir.

János Dezső Aczél, aynı zamanda John Aczel olarak bilinen fonksiyonel denklemler ve bilgi teorisi konusunda uzmanlaşmış Macar-Kanadalı matematikçi.
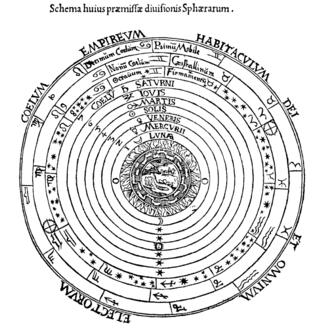
Göksel küreler, Eflâtun, Eudoxus, Aristo, Batlamyus, Kopernik ve diğerleri tarafından geliştirilen kozmolojik modellerin temel unsurlarıydı. Bu kozmolojik modellerde, sabit yıldızların ve gezegenlerin görünen hareketleri, sanki kürelere yerleştirilmiş mücevherler gibi, eterik, şeffaf bir beşinci elementten (esîr) yapılmış dönen kürelere gömülü olarak düşünülmüştür. Sabit yıldızların birbirlerine göre konumlarını değiştirmediğine inanıldığından, bunların tek yıldızlı bir kürenin yüzeyinde olması gerektiği ileri sürülmüştür.

Matematiksel ve teorik biyoloji, biyolojinin bilimsel teorileri kanıtlamak için gerekli deneyleri yapmakla uğraşan deneysel biyoloji dalının aksine biyolojik sistemlerin yapılarının, gelişimlerinin ve davranışlarının altında yatan ilkeleri araştırmak için yaşayan organizmaların teorik analizlerini, matematiksel modellerini ve soyutlamalarını kullanan bir dalıdır. Bu alan aynı zamanda matematiksel yanını vurgulamak için matematiksel biyoloji ya da biyomatematik ya da biyolojik yanını vurgulamak için ise teorik biyoloji olarak da adlandırılır. Teorik biyolojinin odak noktası daha çok biyolojinin teorik ilkelerinin geliştirilmesi iken matematiksel biyoloji biyolojik sistemlerin incelenmesinde matematiği kullanır ama her iki terim de bazen birbirinin yerine kullanılabilmektedir.

Öklid geometrisinde, Batlamyus eşitsizliği, düzlemde veya daha yüksek boyutlu bir uzayda dört nokta tarafından oluşturulan altı uzunluğu ilişkilendirir. Herhangi bir A, B, C ve D noktası için aşağıdaki eşitsizliğin geçerli olduğunu belirtir:
 .
.
Cebirde halka teorisi, toplama ve çarpmanın tanımlandığı ve tamsayılar için tanımlanan işlemlere benzer özelliklere sahip cebirsel yapılar olan halkaların incelenmesidir. Halka teorisi; halkaların yapısını, temsillerini veya farklı dillerde modülleri, özel halka sınıflarını ve homolojik özellikler ve polinom özdeşlikleri gibi uygulamaları inceler.
Matematikte, değişmeli halka, çarpma işleminin değişmeli olduğu bir halkadır. Değişmeli halkaların incelenmesine değişmeli cebir denir. Değişmeli olmayan cebirse, değişmeli halkalara özgü olmayan halka özelliklerinin incelenmesidir. Bu ayrım değişmeli olmayan halkalara uzanmayan değişmeli halkaların temel özelliklerinin çok sayıda olmasından kaynaklanır.

Matematikte, bir kategori, "oklar" ile birbirine bağlanan "nesneler" koleksiyonudur. Bir kategorinin iki temel özelliği vardır. Bunlar okları birleşmeli olarak oluşturma yeteneği ve her nesne için bir birim okunun varlığıdır. Basit bir örnek; nesneleri küme olan ve okları işlev olan kümeler kategorisidir.
Lucy Joan Slater, hipergeometrik fonksiyonlar üzerinde çalışan ve Rogers-Ramanujan Özdeşlikleri'nin birçok genellemesini bulan bir İngiliz matematikçiydi.

Salomon Bochner, matematiksel analiz, olasılık teorisi ve diferansiyel geometri alanındaki çalışmalarıyla tanınan Galiçya doğumlu Amerikalı bir matematikçidir.

 .
.























