Ferroelektrik

Ferroelektrik, harici elektrik alan tarafından muhafaza edilen spontane elektrik polarizasyonuna sahip olan metallerin özelliğidir. Terim olarak, maddelerin kalıcı manyetik moment sergilediği Ferromanyetizmaya benzer şekilde kullanılır. Ferroelektrik 1920'de, Rochelle salt'da, Valasek tarafından keşfedildiğinde, Ferromanyetizma biliniyordu. Bu nedenle, en fazla ferroelektrik özellik gösteren maddeler demir içermemesine rağmen, demir anlamına gelen bir ön ek olan ferro kelimesi kullanıldı.

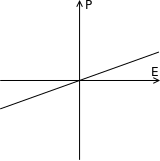
Birçok madde kutuplaşırken,indüklenen (uyarılan) kutuplaşma, harici olarak etki eden elektrik alana neredeyse tamamen eşittir; bu nedenle kutuplaşama lineer (doğrusal) bir fonksiyondur. Bu fonksiyonun grafiği yukarıda (dielektrik polarizasyon) gösterilmiştir. Paraelektrik olarak bilinen bazı maddeler, daha pekiştirilmiş doğrusal olmayan kutuplaşma sergiler. Bu kutuplaşmanın grafiği yukarıdaki şekilde (paraelektrik polarizasyon) gösterilmiştir. Elektriksel geçirgenlik, yalıtkan maddelerde ve harici elektrik alan fonksiyonunda olduğu gibi kutuplaşma eğrisinin eğimine karşılık gelir.

Doğrusal olmamalarına ek olarak; ferroelektrik maddeler, uygulanan elektrik alan sıfır bile olsa, spontane sıfır dışı kutuplaşmayı gösterir. Ferroelektriklerin ayırt edici özelliği  zıt yöndeki spontane kutuplaşmanın, uygun büyüklükteki elektrik alan tarafından muhafaza edilebilmesidir. Bu nedenle, kutuplaşma (polarlaşma) hem elektrik alana hem de döngüde geçen süreye bağlıdır. Bu maddelere ferroelektrik denilmesinin sebebi, benzer süreli döngüye ve spontane mıknatıslanmaya sahip olan ferromanyetik materyallerle benzer olmalarıdır.

Genellikle, maddeler faz değiştirme sıcaklığında ferroelektrik özellik gösterir. Bu sıcaklığa Curie sıcaklığı denir ve maddeler bu sıcaklığın üstünde paraelektriktir, spontane kutuplaşma kaybolur ve ferroelektrik kristali paraelektrik hale dönüşür. Birçok ferroelektrik madde, Curie sıcaklığının üzerinde pizoelektrik (basınçsal elektrik) özelliğini kaybeder çünkü bu maddelerin paraelektrik safhası merkeze göre simetrik kristalografik yapıya sahiptir.^[1]

Doğrusal olmayan yapıdaki ferroelektrik maddeler, kapasitesi ayarlanabilen kondansatör yapımında kullanılır. Genellikle, ferroelektrik kondansatörler bir çift elktrotun arasına konulmuş ferroelektik tabakdan oluşur. Ferroelektriklerin geçirgenliği ayarlanabilir ve özellikle faz geçiş sıcaklığına yaklaştığında çok yüksek bir değere sahiptir. Bundan dolayı, ferroelektrik kondansatörler, aynı kapasiteye sahip dielektrik kapasitörlere kıyasla  küçük ebatlara sahiptir.

Spontane kutuplaşmalı ferroelektrik maddeler,bilgisayarlarda ve RFID kartlarda bulunan ferroelektik RAM yapımında kullanılan ferroelektrik kapasitörlerde,hafıza fonksiyonu olarak kullanılan hysteresis (süre-durum) etkisini gösterir. Bu uygulamalarda ince bir film şeklindeki ferroelektrik malzemeler kullanılır ve bunlar makul voltajı aktarmak için gerekli alanı oluşturur. Ancak, ince film kullanılırken, aygıtların hatasız çalışması için ara yüzlere ve elektrotalara dikkat edilmelidir.^[2]

Ferroelektrik materyallerin piezoelektrik ve pyroelektrik olabilmeleri için simetrik olmaları gerekir. Piezoelektrik, pyroelektrik ve hafıza özelliklerinin birleşimi ferroelektrik kondansatörlerini sensör uygulamaları için çok kullanışlı yapar. Ferroelektrik kondansatörler; ultrason cihazlarında, yüksek kaliteli kızılötesi kameralarda, yangın sensörlerinde, radarlarda, titreşim sensörlerinde ve dizel motorların yakıt enjektörlerinde kullanılır.

Son zamanlarda oluşan bir başka fikirde ferroelektik tünel kavşağıdır (FTJ). FTJ, metal elektrotlar arasına konulmuş nanometrik ferroelektrik filmden oluşur. Ferroelektik katman, elektronların tünel oluşturmasına izin verecek kadar incedir. Kutupsuzlaşma alanının yanı sıra, piezoelektrik ve arayüz etkisi; çok büyük bir elektrodirenç açıp kapama etkisine sebep olabilir.

Araştırmacıların çift manyetik ve ferroelektik şekilde düzenlenmiş materyallerin yollarını aradığı bir başka konu ise multiferroiklerdir. Bu konu hakkına yeniden gözden geçirilmiş birçok görüş bulunmaktadır.^[3]

Ferroelektrik materyallerin dahili elektrik dipolü, materyal örgüsüyle çiftler oluşturur. Bu nedenle, örgüyü değiştiren her şey, aynı zamanda dipolün sağlamlığını; diğer bir deyişle spontane kutuplaşmasını değiştirir. Spontane kutuplaşmadaki değişim, yüzeydeki yüklerin değişimine sebep olur. Bu da ferroelektrik kondansatörlerde, kondansatöre etki eden herhangi bir harici voltaj olmasa bile akımın oluşmasına neden olur. Materyal örgüsünün boyutlarını değiştiren iki etki, kuvvet ve sıcaklıktır. Harici baskı uygulamasına bağlı olan yüzey yükleri üretimine piezoelektrik denir. Sıcaklık değişimine bağlı olan spontane kutuplaşma değişimine pyroelektrik adı verilir.

Genel olarak, kristallerde 32 krisal sınıfında, 230 boş/ara sınıf ve 21 tane merkezi simetrik olmayan grup bulunur ve bunların 20 tanesi pizoelektriktir. Pizoelektrik olanların 10 tanesi spontane elektrik kutuplaşmasına sahiptir. Bunlar sıcaklıkla farklılaştığı için pyroelektrik adını alır. Pyroelektirik materyallerin bazıları ferroelektriktir.

Ferroelektrik faz geçişleri sıklıkla uzanımlı/yer değiştirmeli (BaTiO3 gibi) veya düzenli-düzensiz (NaNO2)olarak sınıflandırılır. Faz geçişleri sıklıkla iki özelliğide gösterir. Baryum titanate tipik bir uzanımlı ferroelectik örneğidir ve faz geçişi polarlaşma dönüm noktası'ndan anlaşılır. Bu noktada iyon denge konumundan biraz uzaklaşır; kristale ait iyonlardan kaynaklanan elektrik alanın sebep olduğu kuvvet, elastik geri yükleme kuvvetinden daha hızlı artar. Bu durum iyonların denge pozisyonunda asimetrik bir değişime ve geçici dipol momentine sebep olur. Baryum titanate'teki iyonic yer değiştirme, sekizgen oksijen kafesinin içindeki titanyum iyonuyla ilişkilidir. Bir başka  ferroelektrik materyal olan lead titanate'in yapısı baryum titanate'e benzemesine rağmen, ferroelektrik için gereken sürücü kuvvet; lead ile oksijen atomlarının arasındaki ilişkiden dolayı karmaşık hale gelir. Düzenli-düzensiz yapıdaki ferroelektriklerde, her bir hücre için bir dipol momenti vardır ancak yüksek sıcaklıklarda gelişigüzel bir dağılım gösterir. Düşük sıcaklıklarda ise, faz geçişi boyunca dipol sırası etkinlik alanının içinde hep aynı yöndedir.

Lead zirconate titanate (PZT), ferroelektrik materyallerin kullanımında önemli bir yere sahiptir. PZT ferroelektrik lead titanate ve ferroelektrik olmayan lead zirconate arasındaki katı çözeltinin parçasıdır. Farklı yapılar; hafıza uygulamaları gibi farklı alanlarda kullanılır. PZT için lead titanate yapılar tercih edilirken, piezoelektrik uygulamalar; 50/50' ye yakın yapıdaki morphotik faz sınırlarıyla ilişkili değişik piezoelektrik katsayılardan oluşturulur.

Ferromanyetiklerde olduğu gibi, ferroelektrik kristaller sıklıkla geçiş sıcaklığı ve alan yapısı süresini gösterir. Bazı ferroelektrik kristallerin geçiş fazının doğası hala tam olarak anlaşılamamaktadır.

1974 yılında, R.B.Meyer simetrik argümanları kullanarak ferroelektrik likit kristaller olabileceğini tahmin etti ve tahmini kısa bir süre içinde simetrik likit kristal fazdaki yatık ferroelektiriklerin davranışlarının gözlemlenmesi sonucunda doğrulandı. Artık teknoloji yatık ekran monitörlerine izin veriyordu. Toplu üretim 1994-1999 yılları arasında Canon tarafından gerçekleştirildi. Ferroelektrik likit kristaller yansıtıcı LCoS yapımında kullanıldı.

2010 yılında, David Field, sıradan kimyasal filmlerin (örneğin; nitrous okside, propan) ferroelektrik özellikte olduğunu keşfetti. Bu yeni ferroelektrik materyal sınıfı spontelektrik özellik gösteriyordu ve nanoteknolojiden, yıldızlar arasındaki toza etki eden elektriğe kadar  geniş bir uygulama alanına sahip oldu.

Diğer ferroelektrik materyaller triglycine sulfate, polyvinylidene fluride ve lityum tantalate içerir..^[4]

${\displaystyle {\begin{array}{ll}\Delta E=&{\frac {1}{2}}\alpha _{0}\left(T-T_{0}\right)\left(P_{x}^{2}+P_{y}^{2}+P_{z}^{2}\right)+{\frac {1}{4}}\alpha _{11}\left(P_{x}^{4}+P_{y}^{4}+P_{z}^{4}\right)\\&+{\frac {1}{2}}\alpha _{12}\left(P_{x}^{2}P_{y}^{2}+P_{y}^{2}P_{z}^{2}+P_{z}^{2}P_{x}^{2}\right)\\&+{\frac {1}{6}}\alpha _{111}\left(P_{x}^{6}+P_{y}^{6}+P_{z}^{6}\right)\\&+{\frac {1}{2}}\alpha _{112}\left[P_{x}^{4}\left(P_{y}^{2}+P_{z}^{2}\right)+P_{y}^{4}\left(P_{x}^{2}+P_{z}^{2}\right)+P_{z}^{4}\left(P_{x}^{2}+P_{y}^{2}\right)\right]\\&+{\frac {1}{2}}\alpha _{123}P_{x}^{2}P_{y}^{2}P_{z}^{2}\end{array}}}$

P_x, P_y ve P_{z,polarlaşma vektörünün bileşenleri ve}  , ${\displaystyle \alpha _{i},\alpha _{ij},\alpha _{ijk}}$ kristal simetridir. Ferroelektriklerdeki diğer oluşum alanlarını  ve olayları anlamak için bu eşitlikler faz alanı modelinde kullanılır. Tipik olarak, serbest enerjiye, elastik, elektrostatik ve gradient terimler eklenir. Bu eşitlikler sınırlı/sonlu farklılık methodunu örgülere ayırmak için ve Gauss's yasası ile doğrusal elastikliğin zıtlıkarını çözmek için kullanılır.

Bilinen bütün ferroelektrikler, ${\displaystyle \alpha _{0}>0}$ ve ${\displaystyle \alpha _{111}>0}$ şeklindedir. Bu katsayılar deneysel olarak veya simülasyonla elde edilebilir.  Ferroelektriklerin birinci faz geçişi için, ${\displaystyle \alpha _{11}<0}$, iken, ikinci faz geçişi için ${\displaystyle \alpha _{11}>0}$ 'dir .

Ferroelektrik için kübik beşgen yapılı faz geçişnin spontane polarlaşması, P_s serbest enerjinin tek boyutlu (1D) tanımı dikkate alınarak elde edilebilir:

${\displaystyle \Delta E={\frac {1}{2}}\alpha _{0}\left(T-T_{0}\right)P_{x}^{2}+{\frac {1}{4}}\alpha _{11}P_{x}^{4}+{\frac {1}{6}}\alpha _{111}P_{x}^{6}}$

Bu serbest enerji, iki serbest enerji minimumu içeren şekle sahiptir. ${\displaystyle P=\pm P_{s}}$, Bu iki minimum nokatada serbest enerjinin türevi sıfırdır :

${\displaystyle {\frac {\partial \Delta E}{\partial P_{x}}}=\alpha _{0}\left(T-T_{0}\right)P_{x}+\alpha _{11}P_{x}^{3}+\alpha _{111}P_{x}^{5}=0}$

${\displaystyle P_{x}\left[\alpha _{0}\left(T-T_{0}\right)+\alpha _{11}P_{x}^{2}+\alpha _{111}P_{x}^{4}\right]=0}$

Ferroelektrik fazda serbest enerji maksimumu P_x = 0 'a karşılık geldiği için, spontane kutuplaşma Ps aşağıdaki gibi elde edilir   :

${\displaystyle \alpha _{0}\left(T-T_{0}\right)+\alpha _{11}P_{x}^{2}+\alpha _{111}P_{x}^{4}=0}$

bu da:

${\displaystyle P_{s}^{2}={\frac {1}{2\alpha _{111}}}\left[-\alpha _{11}\pm {\sqrt {\alpha _{11}^{2}-4\alpha _{0}\alpha _{111}\left(T-T_{0}\right)}}\right]}$

ve çıkarılan sonuç birinci ve ikinci faz geçişleri için negatif kare kök içerir:

${\displaystyle P_{s}={\sqrt {{\frac {1}{2\alpha _{111}}}\left[-\alpha _{11}+{\sqrt {\alpha _{11}^{2}-4\alpha _{0}\alpha _{111}\left(T-T_{0}\right)}}\right]}}}$

Eğer ${\displaystyle \alpha _{11}=0}$ ise, yukarıdaki yaklaşımı kullanarak  spontane kutuplaşma elde edilir:

${\displaystyle P_{s}={\sqrt {-{\frac {\alpha _{0}\left(T-T_{0}\right)}{\alpha _{111}}}}}}$

Süresel döngü (P_x vs E_x)  bir başka elektrostatik terim ekleyerek, serbest enerji genişlemesinden elde edilir.E_x P_x, aşağıdaki gibidir :

${\displaystyle \Delta E={\frac {1}{2}}\alpha _{0}\left(T-T_{0}\right)P_{x}^{2}+{\frac {1}{4}}\alpha _{11}P_{x}^{4}+{\frac {1}{6}}\alpha _{111}P_{x}^{6}-E_{x}P_{x}}$

${\displaystyle {\frac {\partial \Delta E}{\partial P_{x}}}=\alpha _{0}\left(T-T_{0}\right)P_{x}+\alpha _{11}P_{x}^{3}+\alpha _{111}P_{x}^{5}-E_{x}=0}$

${\displaystyle E_{x}=\alpha _{0}\left(T-T_{0}\right)P_{x}+\alpha _{11}P_{x}^{3}+\alpha _{111}P_{x}^{5}}$

Ex grafiği Px fonksiyonu olarak ve 45 derecelik açı ile çizmek için ''S'' şeklinde bir eğri çizgi ile ifade edilir. S'nin merkezi serbest enerji yerel maksimum (çünkü${\displaystyle {\frac {\partial ^{2}\Delta E}{\partial P_{x}^{2}}}<0}$ ). Bu bölgeyi yok edip S' nin alt ve üst parçalarını birleştiren dikey ve sürekli olmayan çizgi döngü süresini verir.