Fermi'nin etkileşimi
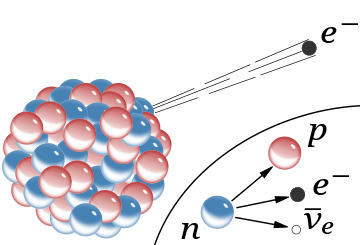
β-
bozunması (Eşlik eden antinötrino çıkarılmıştır). Görsel, bir serbest nötronun beta bozunmasını gösterir. İki olayda da, sanal
W-
bozonunun (daha sonra elektron ve antinötrinoya bozunan) orta düzey yayılımı gösterilmemiştir.
Parçacık fiziğinde, Fermi etkileşimi (aynı zamanda beta bozunmasının Fermi teorisi veya Fermi dörtlü-fermiyon etkileşimi) beta bozunmasının 1933'te Enrico Fermi tarafından önerilmiş bir açıklamasıdır.[1] Teori, dört fermiyonun (ilişkili Feynman diyagramının bir köşesinde) birbiriyle direkt etkileştiğini varsayar. Bu etkileşim bir nötronun bir elektron, bir nötrino (daha sonra bir antinötrino olduğu belirlendi) ve bir protonla doğrudan bağlanmasıyla bir nötronun beta bozunmasını açıklar.[2]
Fermi bu bağlanmadan ilk olarak 1933'te beta bozunmasının tanımını yaparken bahsetti.[3] Fermi etkileşimi, proton-nötron ve elektron-antiötrino arasındaki etkileşimin, Fermi teorisinin düşük enerjili etkili alan teorisi olduğu sanal bir W⁻ bozonunun aracılık ettiği zayıf etkileşim teorisinin habercisiydi.
İlk ret ve sonraki yayın tarihi
Fermi ilk olarak "okuyucunun ilgisini çekemeyecek kadar gerçeklikten uzak spekülasyonlar içerdiği" için reddedilen beta bozunmasının "geçici" teorisini prestijli bir bilim dergisi olan Nature'de yayınladı.[4] Nature daha sonra bu reddi kendi tarihindeki en büyük editör hatalarından biri olduğunu kabul etti.[5] Daha sonra Fermi, revize edilmiş versiyonları İtalyan ve Alman yayıncılara sundu ve yayınlar bunları kabul edip 1933 ve 1934'te bu dillerde yayınladı.[6][7][8][9] Makale, o sırada İngilizce birincil yayında yer almadı.[5] Bu ufuk açıcı makalenin İngilizce çevirisi American Journal of Physics'te 1968 tarihinde yayınlandı.[9]
Fermi fark etti ki makalenin asıl reddini o kadar rahatsız edici buldu ki, teorik fizikten biraz ara vermeye ve sadece deneysel fizik yapmaya karar verdi. Bu, kısa bir süre sonra, yavaş nötronlarla çekirdeklerin aktivasyonu ile ilgili ünlü çalışmasına yol açacaktır.
"Geçici"
Tanımlar
Teori, doğrudan etkileşim içinde olduğu varsayılan üç tür parçacıkla ilgilenir: başlangıçta () "nötron durumu"ndaki bir “ağır parçacık", daha sonra bir elektron ve bir nötrino emisyonu ile "proton durumu" ()'e geçiş yapar.
Elektron durumu
- 'nin tekli-elektron dalga fonksiyonu olduğu ve durağan halleri olduğu yerde:
, Fock uzayına şu şekilde etki eden <span about="#mwt86" class="mwe-math-element" data-mw="{"name":"math","attrs":{},"body":{"extsrc":"s"}}" id="mwWg" typeof="mw:Extension/math"><span class="mwe-math-mathml-inline mwe-math-mathml-a11y" style="display: none;"><math alttext="{\displaystyle s}" xmlns="http://www.w3.org/1998/Math/MathML"> <semantics> <mrow class="MJX-TeXAtom-ORD"> <mstyle displaystyle="true" scriptlevel="0"> <mi>s</mi> </mstyle> </mrow> <annotation encoding="application/x-tex">{\displaystyle s}</annotation> </semantics> </math></span><img alt="s" aria-hidden="true" class="mwe-math-fallback-image-inline" data-cx="{"adapted":false}" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/01d131dfd7673938b947072a13a9744fe997e632" style="vertical-align: -0.338ex; width:1.09ex; height:1.676ex;"></span> durumundaki bir elektronu yok eden operatördür:
, elektron durumu için bir oluşturma operatörüdür:
Nötrino durumu
Benzer olarak,
'nin tekli-nötrino dalga fonksiyonu ve durağan halleri olduğu yerde yukarıdaki gibidir.
, Fock uzayına şu şekilde etki eden durumundaki bir nötrinoyu yok eden operatördür:
, elektron durumu için bir oluşturma operatörüdür.
Ağır parçacık durumu
, Heisenberg tarafından tanıtılan (daha sonra izospin olarak genelleştirildi) bir operatördür ve parçacık bir nötron olduğunda özdeğeri +1 ve parçacık bir proton ise -1 olan bir ağır parçacık durumuna etki eder. Bu nedenle, ağır parçacık durumları, iki sıralı sütun vektörleri ile temsil edilecektir; burada
bir nötronu temsil eder ve
bir protonu temsil eder (temsil edilişte , olağan spin matrisidir).
Ağır bir parçacığı bir protondan nötrona ve tersi yönde değiştiren operatörler sırasıyla şu şekilde temsil edilir:
ve
karşılığı olan , durumunda nötronun karşılığı olan proton için bir eigen fonksiyonudur.
Hamiltonyen
Hamiltonyen, üç parçadan oluşur: özgür ağır parçacıkların enerjisini temsil eden , özgür hafif parçacıkların
enerjisini temsil eden ve etkileşimini veren bir parça.
ve sırayla nötronun ve protonun operatörleridir, Yani eğer ise, 'dir ve eğer ise, 'dir.
Nükleusun Coulomb alanında 'nin durumunda elektron enerjisi ve 'nin o alandaki elektron sayısı olduğu yerde; 'nin durumundaki nötrino sayısı ve 'nin her bir nötrinonun enerjisi olduğu yerde (serbest, düzlem dalga durumunda olduğu varsayılır), yukarıdaki formül ile bulunur.
Etkileşim kısmı, bir elektronun ve bir nötrinonun (şimdi bir antinötrino olarak bilinir) emisyonu ile birlikte bir protonun bir nötrona dönüşümünü temsil eden bir terim ve ayrıca ters işlem için bir terim içermelidir; elektron ve proton arasındaki Coulomb kuvveti, -bozunma süreciyle ilgisiz olduğu için göz ardı edilir.
Fermi, için iki olası değer önerir: ilki, spini görmezden gelen bir göreceli olmayan sürümü:
ve daha sonra, hafif parçacıkların dört bileşenli Dirac spinörleri olduğunu, ancak ağır parçacıkların hızı 'ye görece küçük ve elektromanyetik vektör potansiyeline benzer etkileşim terimlerinin göz ardı edilebileceğini varsayan bir sürüm:
'nin ve 'nin artık dört bileşenli Dirac spinörlerinin olduğu, 'nin, 'nin Hermitgen eşleniğini temsil ettiği ve 'nin aşağıdaki matris olduğu yerde yukarıdaki formül ile bulunur.
Matris elementleri
Sistemin durumu, 'in ağır parçacığın nötron mu yoksa proton mu, 'nin ağır parçacığın kuantum durumu, 'nin durumundaki elektron sayısı ve 'nin de durumundaki nötrino sayısı olduğu yerde demeti ile verilir.
rölativist versiyonunu kullanarak , Fermi, 𝑛 durumunda bir nötron bulunan durum ile elektronsuz durum arasındaki matris elemanını verir. durumunda bulunan nötrinolar . ve bir protonun durumunda olduğu ve bir elektronun ve bir nötrinonun ve 𝜎 durumlarında bulunduğu durum olarak
burada integral, ağır parçacıkların tüm konfigürasyon uzayını kaplar (hariç ). bu hafif parçacıkların toplam sayısının tek (-) veya çift (+) olmasına göre belirlenir.
Değişim olasılığı
Bilinen kuantum karışıklık teorisine göre durumundaki nötronun yaşam süresini hesaplamak için, yukarıdaki matris elementleri, boş elektron ve nötrino durumları üzerinden toplanmalıdır. Elektron ve nötrino ve özfonksiyonlarının çekirdek içinde sabit olduğu varsayılarak basitleştirilir (yani Compton dalga boyları çekirdeğin boyutundan çok daha küçüktür). Bu, şuna yol açar
ve 'in çekirdeğin konumunda değerlendirildiği yerde yukarıdaki şekilde bulunur.
Fermi'nin altın kuralına göre[],bu değişimin olasılığı
'nin proton ve nötron durumlarının enerji farkları olduğu yerde yukarıdaki şekille bulunur.
Bütün pozitif enerjili nötrino spin / momentum yönlerinin (burada 'nötrino durumlarının yoğunluğudur, sonunda sonsuza alınır) ortalamasını alarak
'in nötrinonun kalan kütlesi ve 'nın Dirac matrisi olduğu yerde yukarıdaki değeri elde ederiz.
Bu değişmenin olasılığının 'ın olduğu değerleri için keskin bir maksimuma sahip olduğuna dikkat edilerek, bu[]
'nın ve 'nın için değerleri olduğu yerde yukarıdaki değere sadeleşir.
Fermi, bu fonksiyon hakkında üç açıklama yapmıştır:
- Nötrino durumları serbest kabul edildiğinden, ve böylece sürekli -spektrumundaki üst limit ise değeridir.
- elektronları için -bozunumunun oluşması için proton-nötron enerji farkının olması gerekir.
- Geçiş olasılığındaki
- faktörü normalde 1 büyüklüğündedir, ancak özel durumlarda yok olur; bu, -bozunumu için (yaklaşık) seçim kurallarına yol açar.
Yasaklı değişimler
Yukarıda da not edildiği gibi, ne zaman ve ağır parçacık durumları arasındaki iç çarpımı kaybolursa, ilgili geçiş "yasak" olur (veya, daha doğrusu, 1'e yakın olduğu durumlardan çok daha az olasıdır).
Çekirdeğin, protonların ve nötronların bireysel kuantum durumları açısından tanımlanması iyiyse, nötron durumu ve proton durumu aynı değerde açısal mometuma sahip olmadıkça yok olur; aksi durumda, tüm çekirdeğin bozunumdan önceki ve sonraki açısal momentumu kullanılmalıdır.
Etkisi
Kısa bir süre sonra Fermi'nin makalesi yayımlandı, Werner Heisenberg'ün Wolfgang Pauli'ye[10] yazdığı bir mektupta, çekirdekteki nötrinoların ve elektronların yayımlanması ve soğurulmasının, karışıklık teorisinin ikinci mertebesinde, protonlar ve nötronlar arasında, emisyonun nasıl olduğuna benzer şekilde, bir çekime yol açması gerektiğini ve fotonların absorpsiyonu elektromanyetik kuvvete yol açtığını kaydetti. Kuvvetin formunda olması gerektiğini fark etti, ancak çağdaş deneysel veriler, bir milyon kat çok küçük bir değere yol açtı.[11]
Aynı yılda, Hideki Yukawa bu fikre kapıldı,[12] ancak onun teorisinde nötrinolar ve elektronlar, durağan kütlesi elektrondan yaklaşık 200 kat daha ağır olan varsayımsal yeni bir parçacık ile değiştirildi.[13]
Sonraki gelişmeler
Fermi'nin dörtlü-fermiyon teorisi, zayıf etkileşimi oldukça iyi bir şekilde açıklar. Maalesef, hesaplanan kesit veya etkileşimin olasılığı, enerjisinin karesi olarak büyür. Bu kesit sınırsız büyüdüğü için teori, yaklaşık 100 GeV'den çok daha yüksek enerjilerde geçerli değildir. Etkileşimin gücünü belirten bir GF Fermi sabiti vardır. Bu, sonunda dört fermiyon temas etkileşiminin daha eksiksiz bir teoriyle (UV tamamlama) değiştirilmesine yol açtı —elektrozayıf teoride açıklandığı gibi bir W veya Z bozonunun değişimi.

Etkileşim ayrıca müon bozunmasını, etkileşimin aynı temel gücüne sahip bir müon, elektron-antinötrino, müon-nötrino ve elektronun birleşmesi yoluyla da açıklayabilir. Bu hipotez Gershtein ve Zeldovich tarafından öne sürüldü ve Vektör akımının korunması hipotezi olarak da bilinir.[14]
Orijinal teoride Fermi, etkileşimin biçiminin iki vektör akımının temas kuplajı olduğunu varsaydı. Daha sonrasında, Lee ve Yang tarafından eksenel, pariteyi ihlal eden bir akımın ortaya çıkmasını hiçbir şeyin engellemediğine dikkat çekildi ve bu, Chien-Shiung Wu tarafından yürütülen deneylerle doğrulandı.[15][16]
Fermi sabiti
Fermi sabitinin en kesin deneysel tespiti, GF değerinin karesiyle ters orantılı olan (müon kütlesini W bozonunun kütlesine karşı ihmal ederken) müon ömrünün ölçümleri ile elde edilir.[17] Modern terimlerle, "indirgenmiş Fermi sabiti", yani doğal birimlerdeki sabit[3][18]
değeridir. Burada, g, zayıf etkileşimin çiftlenim sabitidir ve MW ise söz konusu bozunmaya aracılık eden W bozonunun kütlesidir.
Standart Modelde, Fermi sabiti Higgs vakum beklenti değeridir
- .[19]
Daha doğrudan, yaklaşık olarak (standart model için ağaç düzeyi),
Bu, W ve Z bozonları ile arasındaki ilişki kullanılarak Weinberg açısı açısından daha da basitleştirilebilir, böylece
Kaynakça
- ^ Yang (2012). "Fermi's β-decay Theory". Asia Pacific Physics Newsletter. 1 (1): 27-30. doi:10.1142/s2251158x12000045.
- ^ Theory of Fundamental Processes. W. A. Benjamin. 1962. Yazar
|ad1=eksik|soyadı1=(yardım) - ^ a b Introduction to Elementary Particles. 2nd. 2009. ss. 314-315. ISBN 978-3-527-40601-2. Yazar
|ad1=eksik|soyadı1=(yardım) - ^ Inward Bound. Oxford: Oxford University Press. 1986. s. 418. ISBN 0-19-851997-4.
- ^ a b Neutrino. Oxford University Press. 23 Şubat 2012. Erişim tarihi: 5 Mayıs 2017. Yazar
|ad1=eksik|soyadı1=(yardım)[] - ^ "Tentativo di una teoria dei raggi β". La Ricerca Scientifica (İtalyanca). 2 (12). 1933. Birden fazla yazar-name-list parameters kullanıldı (yardım); Yazar
|ad1=eksik|soyadı1=(yardım) - ^ "Tentativo di una teoria dei raggi β". Il Nuovo Cimento (İtalyanca). 11 (1): 1-19. 1934. doi:10.1007/BF02959820. Birden fazla yazar-name-list parameters kullanıldı (yardım); Yazar
|ad1=eksik|soyadı1=(yardım) - ^ "Versuch einer Theorie der beta-Strahlen. I". Zeitschrift für Physik (Almanca). 88 (3–4): 161. 1934. doi:10.1007/BF01351864. Birden fazla yazar-name-list parameters kullanıldı (yardım); Yazar
|ad1=eksik|soyadı1=(yardım) - ^ a b "Fermi's Theory of Beta Decay". American Journal of Physics. 36 (12): 1150-1160. 1968. doi:10.1119/1.1974382. 12 Mayıs 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Ocak 2023. Birden fazla yazar-name-list parameters kullanıldı (yardım); Yazar
|ad1=eksik|soyadı1=(yardım) Includes complete English translation of Fermi's 1934 paper in German - ^ Scientific Correspondence with Bohr, Einstein, Heisenberg a.o. Volume II:1930–1939. Springer-Verlag Berlin Heidelberg GmbH. 1985. Yazar
|ad1=eksik|soyadı1=(yardım) - ^ The Origin of the Concept of Nuclear Forces. Institute of Physics Publishing. 1996. Yazar
|ad1=eksik|soyadı1=(yardım) - ^ "On the interaction of elementary particles. I.". Proceedings of the Physico-Mathematical Society of Japan (İngilizce). 17: 1. 1935. Birden fazla yazar-name-list parameters kullanıldı (yardım); Yazar
|ad1=eksik|soyadı1=(yardım) - ^ The Historical Development of Quantum Theory, Volume 6 Part 2 (1932–1941). Springer. 2001. Yazar
|ad1=eksik|soyadı1=(yardım) - ^ Gerstein (1955). "Meson corrections in the theory of beta decay". Zh. Eksp. Teor. Fiz.: 698-699.
- ^ Lee (1956). "Question of Parity Conservation in Weak Interactions". Physical Review. 104 (1): 254-258. doi:10.1103/PhysRev.104.254.
- ^ Wu (1957). "Experimental Test of Parity Conservation in Beta Decay". Physical Review. 105 (4): 1413-1415. doi:10.1103/PhysRev.105.1413.
- ^ MuLan Collaboration (2007). "Improved Measurement of the Positive-Muon Lifetime and Determination of the Fermi Constant". Physical Review Letters. 99 (3): 032001. arXiv:0704.1981 $2. doi:10.1103/PhysRevLett.99.032001. PMID 17678280. Birden fazla yazar-name-list parameters kullanıldı (yardım); Yazar
|ad1=eksik|soyadı1=(yardım); Yazar eksik|soyadı2=(yardım) - ^ "CODATA Value: Fermi coupling constant". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2015. 11 Aralık 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 31 Ekim 2016.
- ^ Plehn (2005). "Quartic Higgs coupling at hadron colliders". Physical Review D. 72 (5): 053008. arXiv:hep-ph/0507321 $2. doi:10.1103/PhysRevD.72.053008.











































![{\displaystyle H_{\text{int.}}=g\left[Q\psi (x)\phi (x)+Q^{*}\psi ^{*}(x)\phi ^{*}(x)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b1bc38c2db0878585fd0891e8dadde6e92dba26)

![{\displaystyle H_{\text{int.}}=g\left[Q{\tilde {\psi }}^{*}\delta \psi +Q^{*}{\tilde {\psi }}\delta \psi ^{*}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b03c8d3668dbc6810fd1ac03661cfccf273b378a)











































