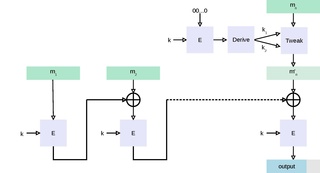
Feistel şifresi

Kriptografide, IBM (ABD) için çalışırken öncü araştırmalar yapan Almanya doğumlu fizikçi ve kriptograf Horst Feistel'in ismiyle anılan Feistel şifresi blok şifrelerin yapımında kullanılan simetrik bir yapıdır; aynı zamanda Feistel ağı olarak da bilinir. Blok şifreler, DES(Data Şifreleme Standardı) dahil, büyük oranda bu şemayı kullanır. Feistel yapısı, şifreleme ve şifre çözme işlemlerinin çok benzer olması, hatta bazı durumlarda aynıdır, sadece anahtar sırasının tersine çevrilmesini gerektirme avantajına sahiptir. Bu nedenle, böyle bir şifreyi uygulamak için gereken kod veya devrenin büyüklüğü neredeyse yarıya inmiştir.

Feistel ağı raund fonksiyonu olarak adlandırılan dahili fonksiyonu ile yinelenen bir şifredir.

Feistel ağları ilk olarak 1973'te Horst Feistel ve Don Coppersmith tarafından tasarlanan IBM'in Lucifer şifresinde ticari olarak görülmüştür. ABD Federal Hükûmeti DES'i (NSA tarafından yapılan değişikliklerle Lucifer'e dayanan bir şifre) kabul ettiğinde Feistel ağları saygınlık kazanmıştır. DES'in diğer bileşenleri gibi, Feistel yapısının iteratif yapısı donanım üzerinde kriptosisteminin daha kolay uygulanmasını sağlamıştır. (özellikle DES'in tasarımında mevcut olan donanım üzerinde).

Birçok modern ve bazı eski simetrik blok şifreleri Feistel ağlarına (örn. GOST 28147-89 blok şifrelemesine) dayanmaktadır ve Feistel şifrelerinin yapısı ve özellikleri, kriptograflar tarafından kapsamlı bir şekilde araştırılmıştır. Özellikle Michael Luby and Charles Rackoff Feistel şifre yapısını analiz etmiştir ve raund fonksiyonunun kriptografik olarak güvenli bir sözderastsal (rastgele) fonksiyon(pseudorandom function) olması durumunda, Ki' nin seed olarak kullanılması ile, 3 devir blok şifresine bir sözderastsal yer değiştirme yapmak için yeterli iken, 4 devir bir "güçlü" sözderastsal yer değiştirme yapmak için yeterlidir. (tersine permütasyona oracle erişimini alan bir düşman için bile sahte bir şekilde kalacağı anlamına gelir.)

Luby ve Rackoff'un bu çok önemli sonucu nedeniyle, Feistel şifrelerine bazen Luby-Rackoff blok şifreleri denir. Daha fazla teorik çalışma, yapıyı biraz genelleştirdi ve güvenlik için daha kesin sınırlar verdi.

F raund fonksiyonu olarak alınır ve sırasıyla devirler 0,1,..,n için K0,K1,..KN de alt anahtarlar olarak alınır.

Daha sonra temel işlem aşağıdaki gibidir:

Şifreli metin blokları 2 eşit parçaya bölünür, (L0,R0)

Her bir devir için i=0,1,..,n hesaplanır

${\displaystyle L_{i+1}=R_{i}\,}$

${\displaystyle R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i}).}$

Şifreli metin ${\displaystyle (R_{n+1},L_{n+1})}$

Şifreli bir metnin ${\displaystyle (R_{n+1},L_{n+1})}$${\displaystyle i=n,n-1,\ldots ,0}$

${\displaystyle R_{i}=L_{i+1}\,}$

${\displaystyle L_{i}=R_{i+1}\oplus \operatorname {F} (L_{i+1},K_{i}).}$

Sonra (L0,R0) tekrar şifresiz metindir.

Feistel'in koyma-yer değiştirme ağlarıyla karşılaştırıldığında avantajlarından birisi raund fonksiyonu olan F'in tersine çevrilmesinin gerekmemesidir.

Diagram hem şifrelemeyi hem de şifre açmayı göstermektedir. Şifre çözme için alt anahtar sırasının tersine çevrildiğine dikkat edilmesi gerekir; bu, şifreleme ve şifre çözme arasındaki tek farktır.

Dengesiz Feistel şifreleri, L0 ve R0'ın eşit uzunluklarda olmadığı modifiye bir yapı kullanır.Skipjack şifresi, böyle bir şifrenin bir örneğidir. Texas Instruments dijital imza aktarıcısı, kimlik sorma-yanıt verme işlemi yapmak için tescilli dengesiz Feistel şifresini kullanır.

Thorp shuffle, bir tarafın tek bir bit olduğu dengesiz bir Feistel şifresinin uç bir örneğidir. Bu, dengeli bir Feistel şifresinden daha kanıtlanabilir güvenlikliğe sahiptir, ancak daha fazla tur gerektirir.

Feistel yapısı blok şifrelerden başka aynı zamanda kriptografik algoritmalarda da kullanılır. Örneğin, en uygun asimetrik şifreleme dolgu (OAEP) şeması, belirli asimetrik anahtar şifreleme şemalarında şifreli metinleri rastgele hale getirmek için basit bir Feistel ağı kullanır.

Genel bir Feistel algoritması, ikinin kuvveti olmayan küçük etki alanlarında güçlü permütasyonlar oluşturmak için kullanılabilir (bkz. Formatı koruyan şifreleme).

Tüm şifre bir Feistel şifresi olsun ya da olmasın, feistel benzeri ağlar şifre tasarımının bir parçası olarak kullanılabilir. Örneğin, MISTY1 devir fonksiyonunda üç aşamalı bir Feistel ağı kullanan bir Feistel şifresidir, Skipjack, G permutasyonunda bir Feistel ağı kullanan modifiye edilmiş bir Feistel şifresidir, Threefish (Skein parçası), feistel benzeri bir MIX işlevi kullanan, feistel olmayan bir blok şifresidir .

Feistel veya değiştirilmiş Feistel:

Genelleştirilmiş Feistel:

• Dizi şifresi

1. Menezes, Alfred J.; Oorschot, Paul C. van; Vanstone, Scott A. (2001). Handbook of Applied Cryptography (Fifth ed.). p. 251. ISBN 0849385237.

2. Luby, Michael; Rackoff, Charles (April 1988), "How to Construct Pseudorandom Permutations from Pseudorandom Functions" 12 Şubat 2019 tarihinde Wayback Machine sitesinde arşivlendi., SIAM Journal on Computing, 17 (2): 373– 386, doi:10.1137/0217022, ISSN 0097-5397

3. Patarin, Jacques (October 2003), Boneh, Dan, ed., "Luby–Rackoff: 7 Rounds Are Enough for 2^n(1−ε) Security" 1 Şubat 2017 tarihinde Wayback Machine sitesinde arşivlendi. (PDF), Advances in Cryptology—CRYPTO 2003, Lecture Notes in Computer Science, 2729: 513–529, doi:10.1007/b11817, retrieved 2009-07-27

4. Zheng, Yuliang; Matsumoto, Tsutomu; Imai, Hideki (1989-08-20). "On the Construction of Block Ciphers Provably Secure and Not Relying on Any Unproved Hypotheses" 9 Haziran 2018 tarihinde Wayback Machine sitesinde arşivlendi.. Advances in Cryptology — CRYPTO’ 89 Proceedings. Springer, New York, NY: 461–480. doi:10.1007/0-387-34805-0_42. Retrieved 2017-11-21.

5. Schneier, Bruce; Kelsey, John (1996-02-21). "Unbalanced Feistel networks and block cipher design" 22 Eylül 2017 tarihinde Wayback Machine sitesinde arşivlendi.. Fast Software Encryption. Springer, Berlin, Heidelberg: 121–144. doi:10.1007/3-540-60865-6_49. Retrieved 2017-11-21.

6. Bono, Stephen; Green, Matthew; Stubblefield, Adam; Juels, Ari; Rubin, Aviel; Szydlo, Michael (2005-08-05). "Security Analysis of a Cryptographically-Enabled RFID Device" (PDF). Proceedings of the USENIX Security Symposium. Retrieved 2017-11-21.

7. Morris, Ben; Rogaway, Phillip; Stegers, Till (2009). "How to Encipher Messages on a Small Domain" 23 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi. (PDF). Advances in Cryptology - CRYPTO 2009. Springer, Berlin, Heidelberg: 286–302. doi:10.1007/978-3-642-03356-8_17. Retrieved 2017-11-21.