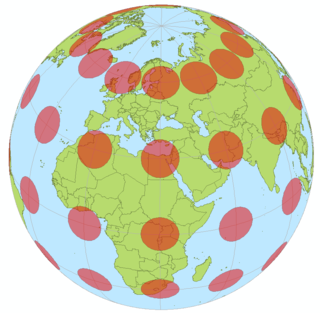
Eşdikdörtgensel izdüşüm

Eşdikdörtgensel izdüşüm (aynı zamanda eşdikdörtgensel projeksiyon, eşmesafeli silindirik izdüşüm veya alakart parallélogrammatique izdüşümü olarak da adlandırılır ve carrée levhası izdüşümünün özel durumunu içerir (aynı zamanda coğrafi izdüşüm, enlem/boylam izdüşümü veya düzlem grafiği olarak da adlandırılır)), Batlamyus'un MS 100 civarında ortaya attığı projeksiyona dayandırılan ve Tire'li Marinus'a atfedilen basit bir harita projeksiyonudur.^[1] Projeksiyon, meridyenleri sabit aralıklı dikey düz çizgilerle (sabit aralıklı meridyen aralıkları için) ve enlem çemberlerini sabit aralıklı yatay düz çizgilerle (sabit paralel aralıkları için) eşler. Projeksiyon ne eşit alana sahiptir ne de konformaldır. Bu projeksiyonun getirdiği çarpıklıklar nedeniyle, navigasyon veya kadastro haritalamada çok seyrek bir şekilde kullanılmaktadır; yaygın olarak tematik haritalamada kullanılır. Özellikle, harita üzerindeki bir görüntü pikselinin konumu ile Dünya üzerindeki karşılık gelen coğrafi konumu arasındaki özellikle basit ilişki nedeniyle carrée levhası, Celestia ve NASA World Wind gibi küresel coğrafi bilgi sistemleri için bir standart haline geldi.

İleri projeksiyon, küresel koordinatları düzlemsel koordinatlara dönüştürür. Geri projeksiyon, düzlemden tekrar küreye dönüşür. Formüller küresel bir modeli varsayar ve şu tanımları kullanır:

${\displaystyle \lambda }$ projelendirilecek yerin boylamı;

${\displaystyle \varphi }$ projelendirilecek yerin enlemi;

${\displaystyle \varphi _{1}}$ projeksiyon ölçeğinin doğru olduğu standart paraleller (ekvatorun kuzeyi ve güneyi);

${\displaystyle \varphi _{0}}$ haritanın merkezi paralelidir;

${\displaystyle \lambda _{0}}$ haritanın merkezi meridyeni;

${\displaystyle x}$ haritada öngörülen konumun yatay koordinatr;

${\displaystyle y}$ haritada öngörülen konumun dikey koordinatı;

${\displaystyle R}$ dünyanın yarıçapı.

Boylam ve enlem değişkenleri burada radyan cinsinden tanımlanır.

${\displaystyle {\begin{aligned}x&=R(\lambda -\lambda _{0})\cos \varphi _{1}\\y&=R(\varphi -\varphi _{0})\end{aligned}}}$

Plate carrée (Fransızca düz kare anlamında) özel bir durumdur ve bu durum için ${\displaystyle \varphi _{1}}$ sıfırdır. Bu projeksiyon, x'i boylamın değeri ve y'yi enlemin değeri olarak eşleştirir ve bu nedenle bazen enlem/boylam veya enlem/boylam(g) projeksiyonu olarak adlandırılır veya "işdüşümsüz" olarak adlandırılır. Bazen "izdüşümsüz" olarak adlandırılmasına rağmen, aslında izdüşümlüdür.

${\displaystyle \varphi _{1}}$ sıfır olmadığı zaman, örneğin ${\displaystyle \varphi _{1}=36}$ olduğu Marinus Projeksiyonu'nda^[2] veya ${\displaystyle \varphi _{1}=(37.5,43.5,50.5)}$ Ronald Miller Projeksiyonu'nda^[3] projeksiyon, belirli ilgi alanlarını gerçek ölçekte gösterebilir.

Elipsoid model için eşit aralıklı paralellere sahip bir projeksiyon mümkün olsa da, bir elipsoid üzerindeki paraleller arasındaki mesafe sabit olmadığı için artık eşit uzaklıkta olmayacaktır. Paralelleri gerçek aralığı yansıtan eşit uzaklıkta bir harita oluşturmak için daha karmaşık formüller kullanılabilir.

${\displaystyle {\begin{aligned}\lambda &={\frac {x}{R\cos \varphi _{1}}}+\lambda _{0}\\\varphi &={\frac {y}{R}}+\varphi _{0}\end{aligned}}}$

• Harita projeksiyonlarının listesi
• Haritacılık
• Cassini projeksiyonu
• Dikdörtgen dünya haritalarının kullanımına ilişkin çözünürlüklü Gall – Peters projeksiyonu
• Mercator projeksiyonu
• Küresel görüntü projeksiyonu

• Global MODIS tabanlı uydu haritası 19 Haziran 2017 tarihinde Wayback Machine sitesinde arşivlendi. Mavi mermer: kara yüzeyi, okyanus rengi ve deniz buzu.
• Radikalcartography.net'teki tüm ortak projeksiyonların örnekleri ve özelliklerinin 25 Nisan 2009 tarihinde Wayback Machine sitesinde arşivlendi. tablosu.
• Panoramik 8 Mart 2021 tarihinde Wayback Machine sitesinde arşivlendi. Eşit Açılı Projeksiyon 8 Mart 2021 tarihinde Wayback Machine sitesinde arşivlendi., PanoTools wiki.
• Proj4'te Eşit Mesafeli Silindirik (Plate Carrée) 29 Mart 2019 tarihinde Wayback Machine sitesinde arşivlendi.