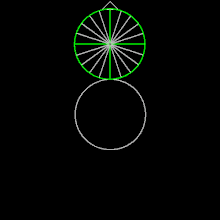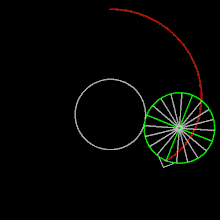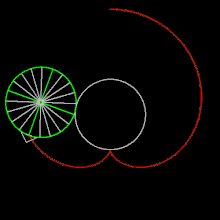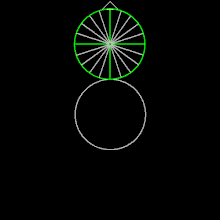
Episikloid

Geometride, bir episikloid (ayrıca hipersikloid olarak da adlandırılır),^[1] sabit bir çemberin etrafında kaymadan yuvarlanan bir çemberin çevresi üzerinde seçilen bir noktanın yolunu izleyerek üretilen bir düzlem eğrisidir -buna episikl (epicycle) denir. Bu, yuvarlanma eğrisinin özel bir türüdür.

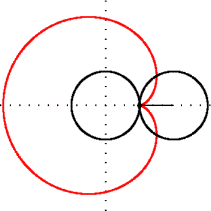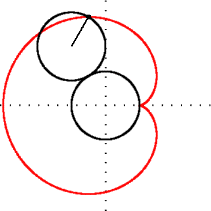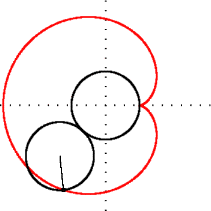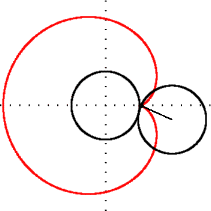
Küçük yarıçapı (R2) 0 olan bir episikloid bir çemberdir. Bu, eğrinin dejenere bir formudur.

Eğer küçük çemberin yarıçapı r ve büyük çemberin yarıçapı R = kr ise, o zaman eğri için parametrik denklemler her iki şekilde de verilebilir:

${\displaystyle {\begin{aligned}&x(\theta )=(R+r)\cos \theta \ -r\cos \left({\frac {R+r}{r}}\theta \right)\\&y(\theta )=(R+r)\sin \theta \ -r\sin \left({\frac {R+r}{r}}\theta \right)\end{aligned}}}$

veya:

${\displaystyle {\begin{aligned}&x(\theta )=r(k+1)\cos \theta -r\cos \left((k+1)\theta \right)\\&y(\theta )=r(k+1)\sin \theta -r\sin \left((k+1)\theta \right)\end{aligned}}}$

Daha özlü ve karmaşık bir biçimde^[2]

${\displaystyle z(\theta )=r\left((k+1)e^{i\theta }-e^{i(k+1)\theta }\right)}$

burada;

• θ açısı devirler halindedir: ${\displaystyle \theta \in [0,2\pi ].}$
• r: daha küçük çemberin yarıçapı
• kr: daha büyük çemberin yarıçapı

(Başlangıç noktasının büyük çember üzerinde olduğu varsayılırsa.) k pozitif bir tam sayı olduğunda, bu episikloidin alanı;

${\displaystyle A=(k+1)(k+2)\pi r^{2}.}$

Bu, episikloidin orijinal sabit çemberden ${\displaystyle {\frac {(k+1)(k+2)}{k^{2}}}}$ kat daha büyük olduğu anlamına gelir.

Eğer k pozitif bir tam sayı ise, o zaman eğri kapalıdır ve k tane köşe noktasına (yani keskin köşelere) sahiptir.

Eğer k bir rasyonel sayı ise, örneğin k = p / q indirgenemez kesir olarak ifade edilirse, eğri p tepe noktasına sahiptir.

p ve q'yu görmek için animasyon döngülerini sayın.

Eğer k bir irrasyonel sayı ise, eğri asla kapanmaz ve büyük çember ile R + 2r yarıçaplı bir çember arasındaki uzayın yoğun alt kümesini oluşturur.

OP (x = 0, y = 0) orijininden (küçük çember üzerindeki p noktasına) olan mesafe yukarı ve aşağı şu şekilde değişir;

${\displaystyle R\leq {\overline {OP}}\leq R+2r}$

burada

• R = büyük çemberin yarıçapı ve
• 2r = küçük çemberin çapıdır.

• Episikloid örnekleri
• 
  k = 1; bir kardioid
• 
  k = 2; bir nefroid
• 
  k = 3; bir trefoiloid
• 
  k = 4; bir quatrefoiloid
• 
  k = 2,1 = 21/10
• 
  k = 3,8 = 19/5
• 
  k = 5,5 = 11/2
• 
  k = 7,2 = 36/5

Episikloid, epitrokoidin özel bir türüdür.

Bir tepe noktası olan episikloid kardioid, iki tepe noktası olan ise nefroiddir.

Bir episikloid ve onun eğeci (evolütü) benzerdir.^[3]

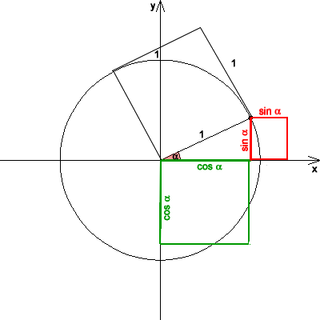
Çözmek istediğimiz şeyin ${\displaystyle p}$ konumu olduğunu, ${\displaystyle \alpha }$'nın teğet noktadan hareketli ${\displaystyle p}$ noktasına olan açı olduğunu ve ${\displaystyle \theta }$'nın başlangıç noktasından teğet noktaya olan açı olduğunu varsayıyoruz.

İki döngü arasında kayma olmadığına göre, o zaman şunu elde ederiz;

${\displaystyle \ell _{R}=\ell _{r}}$

Açının tanımına göre (yarıçap üzerindeki yay oranıdır), o zaman şunu elde ederiz;

${\displaystyle \ell _{R}=\theta R}$

ve

${\displaystyle \ell _{r}=\alpha r}$

Bu iki koşuldan şu özdeşliği elde ederiz;

${\displaystyle \theta R=\alpha r}$.

Buradan, ${\displaystyle \alpha }$ ve ${\displaystyle \theta }$ arasındaki ilişkiyi şu şekilde elde ederiz;

${\displaystyle \alpha ={\frac {R}{r}}\theta }$.

Şekilden, ${\displaystyle p}$ noktasının küçük çember üzerindeki konumunu açıkça görüyoruz.

${\displaystyle x=\left(R+r\right)\cos \theta -r\cos \left(\theta +\alpha \right)=\left(R+r\right)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y=\left(R+r\right)\sin \theta -r\sin \left(\theta +\alpha \right)=\left(R+r\right)\sin \theta -r\sin \left({\frac {R+r}{r}}\theta \right)}$

• Periyodik fonksiyonlar listesi
• Sikloid
• Siklogon
• Taşıyıcı ve episikl
• Episiklik dişli
• Epitrokoid
• Hiposikloid
• Hipotrokoid
• Multibrot seti
• Yuvarlanma eğrisi
• Spirograf

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. ss. 161,168-170,175. ISBN 978-0-486-60288-2. 

• Eric W. Weisstein, Epicycloid (MathWorld)
• "Epicycloid" by Michael Ford, The Wolfram Demonstrations Project, 2007
• O'Connor, John J.; Robertson, Edmund F., "Epicycloid", MacTutor Matematik Tarihi arşivi 
• Animation of Epicycloids, Pericycloids and Hypocycloids
• Spirograph -- GeoFun
• Historical note on the application of the epicycloid to the form of Gear Teeth