Gök mekaniğinde yörünge veya yörünge hareketi, bir gezegenin yıldız etrafındaki veya bir doğal uydunun gezegen etrafındaki veya bir gezegen, doğal uydu, asteroit veya lagrange noktası gibi uzaydaki bir nesne veya konum etrafındaki yapay uydunun izlediği kavisli bir yoldur. Yörünge, düzenli olarak tekrar eden bir yolu tanımlamakla birlikte, tekrar etmeyen bir yolu da ifade edebilir. Gezegenler ve uydular Kepler'in gezegensel hareket yasalarında tanımlandığı gibi, kütle merkezi elips biçiminde izledikleri yolun odak noktasında olacak şekilde yaklaşık olarak eliptik yörüngeleri takip ederler.
Tutulum, ekliptik veya tutulum düzlemi ya da ekliptik düzlem, Dünya'nın Güneş etrafındaki yörünge düzlemidir. Dünya'da bulunan bir gözlemcinin bakış açısından, Güneş'in bir yıl boyunca gök küre etrafındaki hareketi, yıldızların arka planına karşı ekliptik boyunca bir yol izler. Ekliptik önemli bir referans düzlemidir ve ekliptik koordinat sisteminin temelidir.
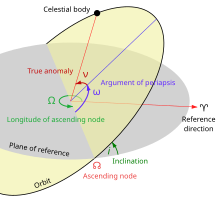
Enberi açısı, ω olarak sembolize edilir ve yörüngede dönen bir cismin Yörünge öğelerinden biridir. Parametrik olarak ω, cismin çıkış düğümünden enberi noktasına kadar olan ve hareket yönünde ölçülen açıdır.
Eris, Güneş Sistemi'nde bilinen en kütleli ve ikinci en büyük cüce gezegendir. Dağınık diskte bulunan bir Neptün ötesi cisimdir (TNO) ve yüksek bir yörünge dışmerkezliğine sahiptir.
Apsis, gök mekaniğinde, eliptik yörüngedeki bir cismin genelde sistemin kütle merkezi durumunda da olan çekim merkezine yörünge boyunca en yakın ve en uzak olduğu noktalara verilen addır.
Karesel genlik modülasyonu iletişim teknolojisinde aynı zamanda iki farklı bilgiyi iletmek amacıyla kullanılan bir modülasyon türüdür..
Gökyüzü koordinat sistemi, gökyüzü konum haritası için kullanılan koordinat sistemidir.
Matematikte, küresel harmonikler Laplace denkleminin çözüm kümesinin açısal kısmıdır. Küresel koordinatların bir sistemi içinde küre yüzeyinde tanımlanır, Fourier serisi ise çember üzerinde tanımlanır. Laplace'ın küresel harmonikleri 
Pierre Simon de Laplace tarafından ilk 1782 yılında tanıtılan bir ortogonal sistemin küresel harmonik formlarının özel bir kümesidir. Küresel harmoniklerden birkaçının kökleri sağda gösterimlenmiştir. Küresel harmonikler pek çok yerde teorik önem taşımaktadır ve özellikle atomik yörünge elektron konfigürasyonları, yerçekimi alanları, geoitleri ve gezegen ve yıldızların manyetik alanlarının temsili ve kozmik mikrodalga arka plan radyasyonu karakterizasyonu hesaplanmasında kullanılan pratik uygulamaları vardır. Küresel harmonikler 3D Bilgisayar grafiklerinde, dolaylı aydınlatma ve 3D şekillerin tanınması gibi konularda geniş bir yelpazede özel bir rol oynamaktadır.
Foton polarizasyonu klasik polarize sinüsoidal düzlem elektromanyetik dalgasının kuantum mekaniksel açıklamasıdır. Bireysel foton özdurumları ya sağ ya da sol dairesel polarizasyona sahiptir. Süperpozisyon özdurumu içinde olan bir foton lineer, dairesel veya eliptik polarizasyona sahip olabilir.
Lamb kayması, adını Willis Lamb'den alan, hidrojen atomunun kuantum elektrodinamiğindeki 2S1/2 ve 2P1/2 enerji düzeyleri arasındaki küçük farklılıktır. Dirac denklemine göre, 2S1/2 ve 2P1/2 orbitalleri (yörüngeleri) aynı enerjiye sahip olmalıdır. Ancak, boşluktaki elektronlar arasındaki etkileşim, 2S1/2 ve 2P1/2 enerji düzeylerinde küçük bir enerji değişimine sebep olur. Lamb ve Robert Retherford bu değişimi 1947'de ölçmüşlerdir ve bu ölçüm, ıraksamayı açıklamak için tekrar normalleştirme teorisine teşvik edici bir unsur olmuştur. Bu, Julian Schwinger, Richard Feynman, Ernst Stueckelberg ve Sin-Itiro Tomonaga tarafından geliştirilmiş modern kuantum elektrodinamiğinin müjdecisiydi. Lamb, 1955 yılında Lamb kayması ile ilgili keşiflerinden ötürü Nobel Fizik Ödülü'nü kazandı.
Fizikte, dairesel hareket bir nesnenin dairesel bir yörünge boyunca bir rotasyon ya da çemberin çevresinde yaptığı harekettir. Rotasyonun sürekli açısal değeriyle birlikte düzgün ya da değişen rotasyon değeriyle düzensiz olabilir. 3 boyutlu bir cismin sabit ekseni etrafındaki rotasyon parçalarının dairesel hareketini içerir. Hareketin denkliği bir cisim kütlesinin merkezini tanımlar.
Birim çember Matematikte, yarıçapı bir birim olan çembere birim çember denir. Çoğunlukla, özellikle trigonometride, Öklid düzlemine göre Kartezyen koordinat sisteminde, merkezi orijin üzerinde (0,0) olan ve yarıçapı bir birim olan çemberdir. n birim çember sıklıkla S1; olarak ifade edilir. Genellikle daha büyük boyutları ise birim küredir. (x, y) birim çember üzerinde bir nokta olduğunda, |x| ve |y|, dik olan ve hipotenüsü bir olan üçgenin diğer kenar uzunluklarıdır. Bu nedenle, Pisagor teoremine göre, x ve y bu denklemi karşılamaktadır.
Yunan harfleri; matematikte, bilimde ve mühendislikte ayrıca sabitler ve özel fonksiyonlar için sembollerle matematiksel notasyonun yapıldığı her yerde, özellikle belirli nicelikleri temsil eden değişkenler için kullanılır. Bu bağlamda, büyük ve küçük harfler farklı ve alakasız şeyleri simgelerler. Latin harfi biçimindeki Yunan harfleri genellikle kullanılmazlar: büyük A, B, E, H, I, K, M, N, O, P, T, X, Y, Z gibi. "i, o ve u" Latin harflerine yakından benzediklerinden, küçük ι (iota), ο (omikron) ve υ (ipsilon) nadiren kullanılır. Bazen Yunan harflerinin değişik fontları matematikte bambaşka semboller için kullanılır, özellikle de φ (fi) ve π (pi).
Yörünge mekaniği veya astrodinamik, roketler ve diğer uzay araçlarının hareketini ilgilendiren pratik problemlere, balistik ve gök mekaniğinin uygulamasıdır. Bu nesnelerin hareketi genellikle Newton'un hareket kanunları ve Newton'un evrensel çekim yasası ile hesaplanır. Bu, uzay görevi tasarımı ve denetimi altında olan bir çekirdek disiplindir. Gök mekaniği; daha genel olarak yıldız sistemleri, gezegenler, uydular ve kuyruklu yıldızlar gibi kütle çekimi etkisinde bulunan yörünge sistemleri için geçerlidir. Yörünge mekaniği; uzay araçlarının yörüngelerine ait yörünge manevraları, yörünge düzlemi değişiklikleri ve gezegenler arası transferler gibi kavramlara odaklanır ve itici manevralar sonuçlarını tahmin etmek için görev planlamacıları tarafından kullanılır. Genel görelilik teorisi, yörüngeleri hesaplamak için Newton yasalarından daha kesin bir teoridir ve doğru hesaplar yapmak ya da yüksek yerçekimini ihtiva eden durumlar söz konusu olduğunda bazen gereklidir.
Güneş geometrisi, güneş ışınları ile yeryüzündeki çeşitli düzenlemelerin yapmış olduğu açıları içerir. Mevsimler, Dünya yüzeyine çarpan güneş radyasyonunun yoğunluğundaki değişikliklerden kaynaklanır. Bu uygulama, enlem ve tarihi değiştirerek ve Güneş açısının ve güneş yoğunluğunun nasıl tepki verdiğini inceleyerek bu değişiklikleri denetlemenizi sağlar.
Çıkış düğümü boylamı, bir nesnenin uzaydaki yörüngesini belirtmek için kullanılan yörünge ögelerinden biridir. Belirtilen bir referans düzleminde ölçüldüğü gibi, boylamın orijini olarak adlandırılan belirli bir referans yönünden çıkış düğümün yönüne olan açıdır. Çıkış düğümü, bitişik görüntüde görüldüğü gibi, nesnenin yörüngesinin referans düzleminden geçtiği noktadır. Yaygın olarak kullanılan referans düzlemleri ve boylamın kökenleri şunları içerir:
- Yer merkezli yörüngeler için, referans düzlemi olarak Dünya'nın ekvator düzlemi ve boylamın başlangıcı olarak Koç'un ilk noktası. Bu durumda boylam, çıkış düğümün sağ açıklığı (RAAN) olarak da adlandırılır. Açı, Koç'un ilk noktasından düğüme doğuya doğru ölçülür. Bir alternatif, uzay aracının ekvatoru geçtiği yerel ortalama zamana dayanan, çıkış düğümün yerel saatidir (LTAN). Diğer gezegenlerin etrafındaki uydular için de benzer tanımlar mevcuttur.
- Güneş merkezli yörüngeler için, referans düzlemi olarak ekliptik ve boylamın başlangıcı olarak Koç'un ilk noktası. Açı, Koç'un ilk noktasından düğüme kadar saat yönünün tersine ölçülür.
- Güneş Sistemi dışındaki yörüngeler için, referans düzlemi olarak ilgi noktasında gökküresine teğet olan düzlem ve kuzey gökyüzü düzlemine) boylamın kökeni olarak. Açı, kuzeyden düğüme doğuya doğru ölçülür., pp. 40, 72, 137; , chap. 17.
Referans düzlemi, gök mekaniğinde yörünge öğelerini tanımlarken kullanılan bir düzlemdir. Referans düzlemine göre tanımlanan iki ana yörünge öğesi yörünge eğikliği ve çıkış düğümü boylamıdır.
Gerçek anomali, gök mekaniğinde Kepler yörüngesinde hareket etmekte olan bir cismin pozisyonunu belirleyen açısal bir parametredir. Gerçek anomali, bir yörüngedeki çeşitli noktaların konumlarını tanımlamak için kullanılan bir terimdir. Enberi noktası yönü ile elipsin ada odağından görünen cismin mevcut konumu yani nesnenin etrafında döndüğü nokta arasındaki açıyı göstermektedir.
Eş-yörüngesel hareket, iki veya daha fazla sayıda astronomik cismin birincil cisim yörüngesiyle aynı veya benzer mesafede bulunan bir yörüngede seyretmesi durumudur. Başka bir deyişle bu cisimler, 1:1 ortalama hareket rezonansında veya ters yönlü ise 1:-1 rezonansındadır.
MS 2. yüzyılda Mısır'da Yunan astronom, coğrafyacı ve jeolog Batlamyus tarafından oluşturulan kirişler tablosu, matematiksel astronomi üzerine bir inceleme olan Batlamyus'un Almagest adlı eserinin Kitap I, bölüm 11'inde yer alan bir trigonometrik tablodur. Esasen sinüs fonksiyonunun değer tablosuna eşdeğerdir. Astronomi de dahil olmak üzere birçok pratik amaç için yeterince kapsamlı olan en eski trigonometrik tablodur. 8. ve 9. yüzyıllardan beri sinüs ve diğer trigonometrik fonksiyonlar, İslam matematiği ve astronomisinde kullanılmış ve sinüs tablolarının üretiminde reformlar yapılmıştır. Daha sonra Muhammed ibn Musa el-Harezmi ve Habeş el-Hâsib bir dizi trigonometrik tablo üretmiştir.
