Emisyon kuramı

Emisyon teorisi, diğer adlarıyla emitör teorisi veya ışığın balistik teorisi 1887'deMichelson-Morley deneyinin sonuçlarını açıklayan, özel izafiyet teorisine rakip bir teoriydi. Emisyon teorileri ışık iletimi için belirli bir çerçevesi olmadığından izafiyet yasalarına uyar, fakat değişmezlik esasını uygulamak yerine ışığın kaynağına bağlı olarakc hızında yayıldığını söyler. Böylece emitör teorisi elektrodinamik ve mekaniği basit bit Newton teorisi ile kombine eder. Temel bilimsel görüşün dışında hala yanlıları olsa da, bu teori bilim adamlarının çoğunluğu tarafından kesinlikle gözden düşmüş sayılmaktadır.^[1][2]

Emisyon teorisi ile en çok anılan isim Isaac Newton’dur. Kendisinin parçacık teorisinde Newton ışık ‘parçacıklarının’ kaynağına bağlı olarak sıcak vücutlardan sembolik bir c hızıyla atıldığını, bu arada genel Newton yasalarına uyduğunu görselleştirmiştir ve biz ışığın bize doğru uzak emitörün hızına bağlı olarak hareket ettiğini varsayarız (c± v).

20. yüzyılda, özel izafiyet Albert Einstein tarafından elektrodinamik veizafiyet prensiplerinin bariz çatışmasını çözmek için yaratıldı. Teorinin geometrik açıdan basitliği ikna ediciydi ve bilim adamlarının çoğu izafiyeti 1911'de kabul etti. Yine de birkaç bilim adamı izafiyetin ikinci temel şartına itiraz etti: ışık hızının tüm eylemsiz çerçevelerde sabit olması. Bu yüzden emisyon teorisinin ışık hızının kaynağın hızına bağlı olduğu değişik tipleri önerildi ve Lorentz dönüşümü yerine Galileo dönüşümü kullanıldı. Hepsi Michelson-Morley deneyinin negatif sonuçlarını açıklayabiliyordu, ışık hızının tüm referans çerçevelerinde interferometreye bağlı olarak sabit olması. O teorilerden bazıları:^[1][3]

• Işık orijinal hareket halindeki kaynağından aldığı hızın bileşenlerini takip ederek yolunu tamamlar ve yansımadan sonra küresel formda orijinal kaynakla aynı hızdaki bir merkez etrafında yayılır (Walt Ritz tarafından 1908 de önerilmiştir).^[4] Bu model en eksiksiz emisyon teorisi olarak dikkate alınmıştır. (Aslında, Ritz Maxwell-Lorentz elektrodinamiğini modeliyordu. Sonraki bir belgede ^[5] Ritz teorisindeki emisyon parçacıklarının yollarındaki yüklerle olan etkileşimden zarar göreceğini bu yüzden dalgaların (onlar tarafından üretilen) orijinal emisyon hızlarını koruyamayacağını söyledi.
• Yansıyan bir aynanın uyarılmış kısmı yeni bir ışık kaynağı olarak davranır ve yansıyan ışık orijinal ışığın kendi kaynağına bağlı olan hızı gibi aynaya bağlı aynı değerde bir c hızına sahiptir. (özel izafiyete destek vermesine rağmen 1910'da Richard Chase Tolman tarafından tasarlanmıştır.).^[6]
• Aynadan yansıyan ışık kaynağın aynadaki görüntüsünün hızına eşit bir hız bileşeni kazanır. (Oscar M.Stewart tarafından 1911'de tasarlanmıştır.).^[7]
• • Ritz-Tolman teorisinin bir modifikasyonu J.G. Fox tarafından açıklanmıştır (1965). Fox sönme teorisinin (örneğin, ışığın yeniden oluşmasının çapraz ortamda olması) göz önünde bulundurulması gerektiğini savunmuştur. Havada, sönme mesafesi yalnızca 0.2 cm olacaktır, yani bu uzaklığı çaprazlayınca ışığın hızı ilk ışık kaynağına değil ortama bağlı bir sabit olacaktır. (Fox'un kendisi, özel izafiyeti destekliyordu.)^[1]

Albert Einstein’ın kendiemisyon teorisi üzerinde onu özel izafiyet teorisinin himayesinden çıkarmadan önce çalıştığı düşünülmektedir. Yıllar sonra R.S Shankland Einstein’ ın Ritz teorisinin ‘çok kötü’ olduğunu ve kendisinin emisyon teorisinden herhangi bir diferansiyel formunun teoriyi açıklayamadığını, bu yüzden ışık dalgalarının ‘tamamen karıştığını’ düşündüğü için vazgeçtiğini söylediğini bildirmiştir.^[8][9][10]

Aşağıdaki eşitlikler emisyon teorilerini test etmek için de Sitter^[11] tarafından ortaya koyulmuştur:

${\displaystyle c'=c\pm kv\,}$

c ışık hızıdır, v kaynağın hızıdır, c' çıkan ışığın hızıdır ve k 0 ve 1 arasında değerler alabilen ve kaynağa bağımlılık boyutunu gösteren bir sabittir. Emisyon teorileri değerin 1 e kadar çıkmasına izin verirken özel izafiyete ve değişmez esire(ağırlıksız töze) göre, k=0 dır. ‘Işık sürüklenmesinin’ veya söndürme efektinin olmadığı çok kısa mesafelerde sayısız karasal deneyler yapıldı ve sonuçta emisyon teorisi kesin bir şekilde inkâr edilerek ışık hızının kaynağın hızından bağımsız olduğu kanıtlandı

1910 yılında Daniel Frost Comstock ve 1913 yılında Willem de Sitter, ikili yıldız sistemi hakkında görünen yıldızdan gelen ışık iç taraftaki partnerinden gelen ışıktan daha hızlı olabilir ve onu geçebilir diye yazdılar. Eğer mesafe yeterince iyi olsaydı, görünen yıldızın'hızlı' ışığı iç taraftayken yaydığı ‘yavaş’ ışığı yakalayıp geçebilirdi ve yıldız sisteminin görüntüsü tamamen karmaşık bir biçimde ortaya çıkardı. De Sitter üzerinde çalıştığı hiçbir yıldız sisteminin bu ekstrem optik davranışı göstermediğini savundu ve bu Ritz teorisi ve olarak emisyon teorisi için ölüm çanları olarak addedildi. (${\displaystyle k<2\times 10^{-3}}$).^[11][12][13]

de Sitter'in deneye tükenme etkisi Fox tarafından ayrıntılı olarak kabul edilir ve bu muhtemelen ikili yıldızlı dayanan de Sitter tipi kanıt inandırıcılığa zayıflatmaktadır edilmiştir. Bununla birlikte, benzer gözlemler sonucu etkilemeyecek gerektiği yeterince uzun bir yok olma mesafeye sahip Brecher (1977), X-ışını spektrumunda daha yakın yapılmıştır. gözlemler, ışığın hızı kaynağının hızından bağımsız olduğunu teyit etti ${\displaystyle k<2\times 10^{-9}}$.^[2]

Hans Thirring 1926'da emisyon işlemi sırasında güneşteki termal çarpışmalar tarafından hızlandırılan bir atomun, başlangıç ve son noktadaki hızları farklı olan ışık ışınları yaydığını iddia etmiştir. Bu sayede ışık ışınının ucu diğer kısımları geride bırakabilir ve netice olarak dünyaya ulaşana kadar aradaki mesafe 500 km ye kadar uzayabilir, güneş radyasyonunda kendiliğinden oluşan keskinspektral doğrular balistil modeli çürütür..^[14]

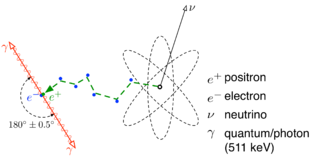
Sadeh (1963) 'in pozitron imhasından türeyen ve zıt yönlerde hareket eden fotonlar arasındaki hız farklarını ölçmek için kullandığı uçuş zamanını tekniğini de içeren deneyleri vardır.^[15] Diğer bir deney Alvager(1963) tarafından yönetilmiştir. Alvager sabit veya hareket eden kaynaklardan gama ışınlarının uçuş zamanlarını karşılaştırmıştır.^[16] İki deney de izafiyete paralel olarak bir fark bulamamıştır.

Filippas ve Fox (1964)^[17] Sadeh ve Alvager'in söndürme efektini tam olarak hesaba katmadıklarını düşünmediler ve bu ikili özellikle söndürme efekti hesabı için tasarlanmış bir deney yaptılar. Çeşitli dedektör-hedef uzaklarından toplanan sonuçlar ışık hızı ile kaynak hızının bir bağlantısı olmadığını kesin olarak gösterdi ve c ± v nin davranışını söndürme ve söndürmesiz olarak tutarsız bir şekilde ele aldı. .

Önceki araştırmalarını devam ettiren Alvager (1964) ışık hızının %99.9 unda fotonlara ayrışan π0 mezonlarını gözlemledi. Deney gösterdi ki fotonlar kaynaklarının hızını kazanmadı ve hala ışık hızıyla hareket etti(). Fotonlar tarafından çizilen görüntü söndürme payının sonucu dikkate değer derecede etkileyemeyeceğini gösterdi.^[18]

Bundan başka nötrino hız ölçümleri yapıldı. Kaynak olarak ışık hızına yakın hızlarda hareket eden mezonlar kullanıldı. Nötrinolar yalnızca zayıf elektronik etkileşimde bulunduğundan söndürme efekti bir rol oynamadı. Karasal ölçümler üst limitini şart koydu.

Sagnac efekti dönen bir platform üzerindeki elektron demetinin diğer demetten daha az mesafe kapsayarak girişim modelinde bir değişiklik yarattığını gösterir. George Sagnac'ın orijinal deneyi sönme etkilerinden zarar görmüş, fakat ondan sonra Sagnac efekti vakumlu yani sönme etkilerinin rol oynamadığı bir alanda meydana gelmiştir.^[19][20]

Emisyon teorisinin Ritz versiyonun tahminleri hareket halindeki ortamda ışığın yayılmasını içeren neredeyse tüm karasal interferometrik testler hakkında tutarlıydı ve Ritz testler tarafından ortaya konan zorlukların Fizeau deneyleri gibi aşılmaz olabileceğini düşünmemiştir. Neyse ki Tolman, Michelson-Morley deneyinin yeryüzü dışından bir ışık kaynağı kullanılarak yapıldığında Ritz hipotezine kesin bir test sağladığını belirtmiştir. 1924'te Dayton Miller güneş ışığını kullanırken Rudolf Tomaschek geliştirilmiş yıldız ışığını kullanarak bir Michelson-Morley deneyi yapmıştır. İki deney de Ritz hipotezi konusunda tutarsızdır.^[21]

Babcock ve Bergman (1964) dönen cam plakaları ortak yol interferometresinin aynaları arasına yerleştirdi ve durgun bir Sagnac Konfigürasyonu kurdu. Eğer cam plakalar yeni bir ışık kaynağı gibi davranırsa yüzeylerinden çıkan ışığın toplam hızı c+v olmalı, girişim modelinde bir değişim olmalıydı. Ancak yine özel izafiyeti doğrulayan ve ışık hızının kaynaktan bağımsızlığını kanıtlayan bir etki görülmedi. Deney havasız ortamda yapıldığınan söndürme etkisi rol oynamadı.^[22]

Albert Abraham Michelson (1913) ve Quirino Majorana (1918/9) hareket etmeyen kaynaklar ve hareket eden aynalarla (ve tam tersi şekilde) interferometre deneyleri yaptılar ve havada ışık hızının kaynağa bağımlı olmadığını gösterdiler. Michelson'un düzenlemesi hareketli aynalarla ışığın üç muhtemel etkileşimini ayırt etmek için dizayn edilmişti. (1) ışık zerrecikleri elastik duvardan yansıyan mermi gibi yansır. (2) ayna yüzeyi yeni bir kaynak gibi davranır. (3) ışığın hızı kaynağın hızından bağımsızdır. Sonuçlar ışık hızının kaynaktan bağımsız olduğu konusunda tutarlıydı.^[23] Marojana hareket eden kaynak ve aynalardan gelen ışığı dalgaboyu değişimlerine oldukça hassas bir eşit olmayan kollu Michelson interferometresi kullanarak analiz etti. Emisyon teorisi hareketli bir kaynaktan çıkan ışığın Doppler değişiminin dalga boyu aynı kalmak şartıyla bir frekans değişimi olduğunu savunur. Ancak, Marojana Emisyon teorisine aykırı olarak dalga boyu değişimleri tespit etmiştir.^[24][25]

Beckmann ve Mandics (1965)^[26] Michelson (1913) ve Marojana(1918) nın hareket eden ayna deneylerini yüksek vakumda k değerini 0.09'dan düşük bularak tekrar ettiler. Uygulanan vakumun söndürme efektini tamamen saf dışı bırakamaması negatif sonuçlar için bir sebepti. Hareketli aynadan gelen ışık bir Lloyd interferometresinden geçti, elektron demetinin fotografik filme gittiği kısım, Lloyd aynasından yansıdığı kısım. Bu deney varsayımsal olarak hareket eden aynalardan gelen c+v hızındaki ışığı ve Lloyd aynasından çıkan c hızındaki ışığı karşılaştırdı.

Emisyon teorileri çerçeve değiştirirken zaman koordinatlarının değişmez olduğu Galileo dönüşümlerini kullanır (salt zaman). Böylece rölativistikzaman genişlemesini doğrulayan Ives–Stilwell deneyi aynı zamanda ışığın emisyon teorisini de çürütür. Howard-Percy Robertson tarafından gösterildiği gibi, Ives–Stillwell deneyi Michelson- Morley deneyi ve Kennedy-Thorndike deneyi ile birlikte düşünüldüğünde Lorenz dönüşümünün tamamı türevlenebilir.^[27]

Ayrıca kuantum elektrodinamiği ışık yayılmasını tamamiyle farklı ancak hala rölativistik ve ışık hızının kaynağa bağlı olduğunu şart koşan hiçbir teoriyle tamamen uyumlu olmayan bir içeriğe yerleştirir

• Özel Görelilik Kuramı Tarihi

• Isaac Newton, Philosophiæ Naturalis Principia Mathematica
• Isaac Newton, Opticks

• Sitter (1913) kağıtlar üzerinde çift yıldızlar gibi kanıt karşı Ritz emisyon teorisi.
• de Sitter (1913) papers on binary stars as evidence against Ritz's emission theory.