
Matematikte türev, bir fonksiyonun tanımlı olduğu herhangi bir noktada değişim yönünü veya hızını veren temel bir kavramdır. Tek değişkenli bir fonksiyonun tanım kümesinin belli bir noktasında türevi, fonksiyonun grafiğine bu noktada karşılık gelen değerde çizilen teğet doğrunun eğimidir. Teğet doğru, tanım kümesinin bu noktasında fonksiyonun en iyi doğrusal yaklaşımıdır. Bu nedenle türev genellikle anlık değişim oranı ya da daha açık bir ifadeyle, bağımlı değişkendeki anlık değişimin bağımsız değişkendeki anlık değişime oranı olarak tanımlanır. Bir fonksiyonun türevini teorik olarak bulmaya türev alma denilir. Eğer bir fonksiyonun tanım kümesindeki her değerinde hesaplanan türev değerlerini veren başka bir fonksiyon varsa, bu fonksiyona eldeki fonksiyonun türevi denir.

Atalet momenti veya eylemsizlik momenti, dönmekte olan bir cismin, dönme hareketine karşı durmasına eylemsizlik momenti denir. Eylemsizlik momenti, toplam dönme hareket gücüne karşı direnç oluşturur ve bu yüzden cisim, tam verimde dönemez.

Yarıçap, bir daire veya kürenin özeğinin (merkezinin) çemberine olan mesafesidir. Çapın yarısına eşittir.

Matematikte karmaşık bir fonksiyonun Laurent serisi bu fonksiyonun negatif dereceli terimler de içeren kuvvet serisi temsilidir. Karmaşık fonksiyonların Taylor serileri açılımının mümkün olmadığı durumlarda bu fonksiyonları açıklamak için de kullanılabilir. Laurent serisi ilk defa 1843'te Pierre Alphonse Laurent tarafından yayınlanmış ve bu matematikçinin adını almıştır. Karl Weierstrass 1841'de bu seriyi bulmuş olabilir ancak o zamanda ilk yayınlayan olamamıştır.
Çukur ayna üzerine gelen ışınları belli bir noktada toplayan ayna.
Açısal hız, bir objenin birim zamandaki açısal olarak yer değiştirme miktarına verilen isimdir. Açısal hız vektörel olup bir cismin bir eksen üzerindeki dönüş yönünü ve hızını verir. Açısal hızın SI birimi radyan/saniyedir, ancak başka birimlerde de ölçülebilir. Açısal hız genellikle omega sembolü ile gösterilir. Açısal hızın yönü genellikle dönüş düzlemine diktir ve sağ el kuralı ile bulunabilir.

Değişken indis optiği, kırıcılık indisi kendi içinde değişen merceklerin üretimini ve niteliklerini inceleyen bir bilim dalıdır. Bu mercekler şekilleri üzerinde bir değişiklik yapılmaksızın sıradan küresel merceklerde oluşan aberasyonları giderebilir. Değişken indisli mercekler küresel, eksenel ve açısal kırıcılık derecelerine sahip olabilir.

Newton halkaları, ışığın iki yüzey, tipik olarak küresel bir yüzey ve bitişik dokunan düz bir yüzey, arasındaki yansımasıyla bir girişim deseninin oluşturulduğu bir olgudur. Bu konu hakkında ilk niceliksel incelemeleri yapan İngiliz fizikçi Isaac Newton tarafından 1666 yılında keşfedildi. Dışbükey bir cam parçası tümsek yüzü aşağıya gelecek şekilde düz bir cam üzerine yerleştirildiğinde, iki parça arasında bir hava katmanı oluşur. Bu hava katmanı ve tümsek merceğin değişen kalınlığı, merkezden itibaren yarımsal dalga boyu kaymalarına neden olur. Bu sisteme ışık gönderilirse merceğin değme noktası merkez olmak üzere eş merkezli çemberler oluşur. Oluşan bu konsantrik halkaların üst üste geldiği ve tepe noktalarının çakıştığı yerde ışık parlaklaşır; ancak tepe ve çukur noktalarının kesiştiği yerde ışık yok olur. Yansıyan ve kırılan ışıktan oluşan bu desenler birbirinin tamamlayıcısıdır. İşte oluşan bu girişim desenine Newton halkaları denir. İki halka arasındaki uzaklık λ, eğrilik yarıçapları R, N ise görünen parlak halka sayısıdır. Aşağıdaki formülle oluşan desenin incelemesi yapılabilir:


Mercek ya da lens ışığın yönünü değiştiren (kıran), ışık ışınlarını birbirine yaklaştıran ya da uzaklaştıran optik alet.
Basit mercek tek bir optik elemanın kullanıldığı, bileşik mercek ise iki optik elemanın bir arada olduğu mercek tipidir. Bileşik mercek, basit mercek kullanıldığında ortaya çıkan sapınç olayının etkisini azaltmak için kullanılır. Mercekler genelde camdan ve saydam plastikten yapılır. Lensler, gereken şekle göre taşlanır, parlatılır veya kalıplanır. Bir mercek, ışığı odaklamadan kıran bir prizmadan farklı olarak, bir görüntü oluşturmak için ışığı odaklayabilir. Mikrodalga lensler, elektron lensler, akustik lensler veya patlayıcı lensler gibi görünür ışık dışındaki dalgaları ve radyasyonu benzer şekilde odaklayan veya dağıtan cihazlara da "mercekler" denir.
Fizikte, dairesel hareket bir nesnenin dairesel bir yörünge boyunca bir rotasyon ya da çemberin çevresinde yaptığı harekettir. Rotasyonun sürekli açısal değeriyle birlikte düzgün ya da değişen rotasyon değeriyle düzensiz olabilir. 3 boyutlu bir cismin sabit ekseni etrafındaki rotasyon parçalarının dairesel hareketini içerir. Hareketin denkliği bir cisim kütlesinin merkezini tanımlar.

Optik teleskoplar esas olarak elektromanyetik spektrumun görünür ışık kısmından ışığı toplayan ve odaklayan teleskop çeşididir. Kullanım amacı bakılan nesnenin doğrudan görünümü için büyütülmüş görüntüsünü oluşturmak, fotoğrafını çekmek ya da elektronik görüntü sensörleri üzerinden veri toplamaktır.Optik teleskop, başlıca elektromanyetik spektrumun görünür bölgesinden olmak üzere direkt görüş için büyütülmüş bir imaj oluştururken, bir fotoğraf yaratırken ya da elektronik imaj sensörleri boyunca veri toplarken ışığı odaklar ve toplar.
Geometrik optik veya ışın optiği, ışık yayılmasını ışınlarla açıklar. Geometrik optikte ışın bir soyutlama ya da enstrumandır; ışığın belirli şartlarda yayıldığı yola yaklaşmada kullanışlıdır.

Magnifikasyon bir şeyin fiziksel boyutunu değil, yalnızca görünüşünü büyütme işlemidir. Bu büyütme işlemi hesaplanmış bir sayı olan ve yine ‘magnifikasyon (büyütme)’ olarak adlandırılan bir değerle gösterilir. Bu sayı 1'den küçük olduğunda, bazen minifikasyon veya de-magnifikasyon olarak adlandırılan, boyutlarda bir azalmaya tekabül eder.
Fourier optiği dalgaların yayılma ortamını kendisinin doğal modu olduğunu kabul etmek yerine, belirli bir kaynağa sahip olmayan düzlemsel dalgaların üstdüşümlerin olarak addeden Fourier dönüşümlerini kullanan klasik optiğin bir çalışma alanıdır. Fourier optiği, dalgayı patlayan bir küresel ve fiziksel olarak Green's fonksiyon denklemleriyle tanımlanabilen tanımlanabilen ve bu kaynağından dışarıya ışıma yapan dalganın üstdüşümü olarak adddeden Huygens-Fresnel prensibinin ikizi olarak da görülebilir.

Renksemez mercek veya akromat, kromatik ve küresel sapmaların etkilerini sınırlandırmak üzere tasarlanmış bir mercektir. Akromatik mercekler iki dalga boyunu aynı düzlemde odaklamaya getirmek için düzeltilir. Akromatın en yaygın türü, farklı miktarlarda dağılım gösteren camlardan yapılmış iki ayrı mercekten oluşan akromatik bir çift parçadır. Tipik olarak, bir element, nispeten yüksek dağılıma sahip olan F2 gibi flint camdan yapılmış bir negatif (içbükey) elemandır ve diğeri daha düşük dispersiyona sahip BK7 gibi taç camından yapılmış bir pozitif (dışbükey) elemandır. Mercek elemanları, birbirine bitişik olarak monte edilmekte, çoğunlukla birbirine yapıştırılmakta ve birinin renk sapmaları diğeri tarafından dengelenene kadar şekillendirilmektedir. En yaygın tipte olanda (gösterilen), taç lens elemanının pozitif gücü, flint cam lens elemanının negatif gücü ile tamamen eşit değildir. Birlikte, ortak bir odaklamaya iki farklı dalga boyu ışık getirecek zayıf bir pozitif lens oluştururlar. Negatif güç unsurunun hâkim olduğu negatif çiftler de yapılır.

Geometride, konik sabit, konik kesitleri tanımlayan bir büyüklüktür ve K harfiyle gösterilir. Tanımı şöyledir:


Optikte, küresel aberasyon , küresel yüzeylere sahip elemanlara sahip optik sistemlerde bulunan bir sapma türüdür. Lensler ve kavisli aynalar başlıca örneklerdir çünkü bu şeklin üretimi daha kolaydır. Merkez dışında küresel bir yüzeye çarpan ışık ışınları, merkeze yakın gelenlerden daha fazla veya daha az kırılır veya yansıtılır. Bu sapma, optik sistemler tarafından üretilen görüntülerin kalitesini düşürür.

Adını Joseph Petzval'den alan Petzval alan eğriliği, optik eksene dik olan düz bir nesnenin düz bir görüntü düzleminde düzgün bir şekilde odağa getirilemediği optik sapmayı tanımlar. Alan eğriliği bir alan düzleştirici kullanılarak düzeltilebilir, tasarımlar ayrıca odak yüzeyindeki görüntü kalitesini iyileştirmek için insan gözünde olduğu gibi kavisli bir odak düzlemi içerebilir.
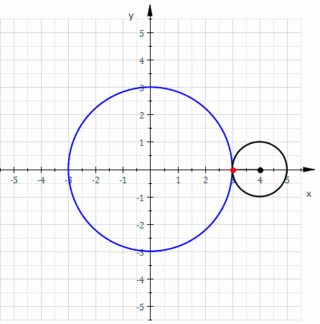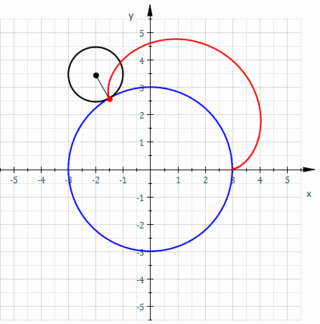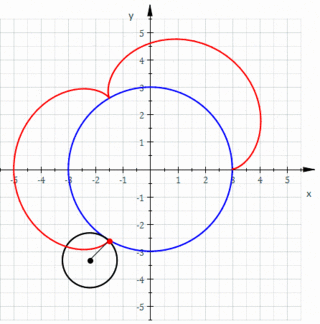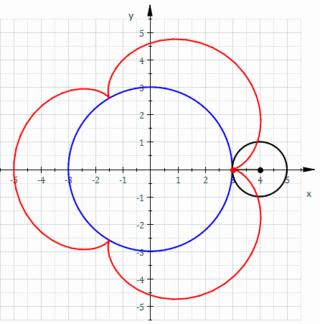
Geometride, bir episikloid, sabit bir çemberin etrafında kaymadan yuvarlanan bir çemberin çevresi üzerinde seçilen bir noktanın yolunu izleyerek üretilen bir düzlem eğrisidir -buna episikl (epicycle) denir. Bu, yuvarlanma eğrisinin özel bir türüdür.

Düzlem ve katenoidden sonra helis yüzey de denen helikoid bilinen üçüncü minimal yüzeydir. Helikoid, helis ve eksenle tanımlanan yüzeydir.























