
Elektriksel işaretlerin ölçülüp değerlendirilmesinde kullanılan aletler içinde en geniş ölçüm olanaklarına sahip olan osiloskop, işaretin dalga şeklinin, frekansının ve genliğinin aynı anda belirlenebilmesini sağlar. Dalga şeklini grafik olarak ekranda gösterir. Yani elektrik dalga sinyali çizer. Dalga sinyalinin, frekansını ve genliğini de öğrenmemizi sağlar. Osiloskop bir elektrik devresine her zaman paralel bağlanır. Çünkü iç direnci çok yüksektir.

Başlangıçta sonsuz küçük hesap veya "sonsuz küçüklerin hesabı" olarak adlandırılan kalkülüs, geometrinin şekillerle çalışması ve cebirin aritmetik işlemlerin genellemelerinin incelenmesi gibi, kalkülüs sürekli değişimin matematiksel çalışmasıdır.
Porte ya da dizek, üzerine notaların yerleştirildiği, 4 eşit aralık ve birbirine paralel 5 çizgiden ve bir donanım bölümünden oluşan şekildir. Genelde portenin donanımına değiştirici diyez veya bemol işaretleri, ritim rakamları yazılır. Notaların üzerine yazıldığı eşit aralıklı beş çizgi ve dört aralıktan oluşan şekle porte (dizek) denir. Çizgiler aşağıdan yukarıya doğru sayılır.
Matematikte sonuşmaz veya asimptot, belirli bir A eğrisine istenildiği kadar yaklaşabilen ikinci bir B eğrisine verilen addır. Bir başka deyişle, A üzerinde ilerledikçe, A ve B arasındaki mesafe azalır ve sıfıra yaklaşır. Asimptot kelimesi, Yunanca "beraber düşmek" anlamındaki simpiptein fiilinin olumsuz halinden türemiştir.
Olasılık kuramı ve bir dereceye kadar istatistik bilim dallarında basıklık kavramı 1905da K. Pearson tarafından ilk defa açıklanmıştır. Basıklık kavramı bir reel değerli rassal değişken için olasılık dağılımının, grafik gösteriminden tanımlanarak ortaya çıkarılan bir kavram olan, sivriliği veya basıklığı özelliğinin ölçümüdür. Basıklık kavramının ayrıntıları olasılık kuramı içinde geliştirilmiştir. Betimsel istatistik için bir veri setinin basıklık karakteri pek dikkate alınmayan bir özellik olarak görülmektedir. Buna bir neden parametrik çıkarımsal istatistik alanında basıklık hakkında hemen hemen hiçbir kestirim veya sınama bulunmamasındandır ve pratik istatistik kullanımda basıklık pek önemsiz bir karakter olarak görülmektedir. Belki de basıklık ölçüsünün elle hesaplanmasının hemen hemen imkânsızlığı buna bir neden olmuştur.
Olasılık kuramı ve istatistik bilim dallarında birikimli dağılım fonksiyonu bir reel değerli rassal değişken olan Xin olasılık dağılımını tümüyle tanımlayan bir fonksiyondur. Olasılık dağılım fonksiyonu veya sadece dağılım fonksiyonu olarak da anılmaktadır. Her bir reel sayı olan x için X'in birikimli dağılım fonksiyonu şöyle ifade edilir:


Matematikte bir çizgi integrali, integrali alınan fonksiyonun bir eğri boyunca değerlendirildiği integraldir. Çeşitli farklı çizgi integralleri kullanılmaktadır. Kapalı eğrinin kullanıldığı durumlarda integrale kontür integrali denildiği de olmaktadır.

Matematikte verilmiş bir fonksiyonun tanım kümesi, fonksiyonun tanımlı olduğu "girdi" değerlerinin oluşturduğu kümedir. Örneğin, kosinüsün tanım kümesi gerçel sayılar olurken karekök fonksiyonunun tanım kümesi 0 ve 0'dan büyük sayıların oluşturduğu negatif olmayan gerçel sayılar kümesidir. Fonksiyonun xy Kartezyen koordinat sistemindeki temsilinde, tanım kümesi x-ekseni (apsis) ile temsil edilir.

Matematikte verilmiş bir fonksiyonun değer kümesi, fonksiyonun tanımlı olduğu "çıkış" değerlerinin oluşturduğu kümedir. Örneğin, kosinüsün değer kümesi [-1; 1] gerçel sayılar aralığıyken gerçel sayılarda karekök fonksiyonunun değer kümesi bütün gerçel sayılardır. Fonksiyonun xy Kartezyen koordinat sistemindeki temsilinde değer kümesi y-ekseniyle (ordinat) temsil edilir.
Bir mal veya bir hizmetin marjinal faydası, ekonomi biliminde neoklasik değer kuramının ana kavramıdır. Bu kavram, eğer diğer her mal ve hizmet tüketiminin ve ilgili verilerin sabit kaldığı varsayılırsa, incelenmekte olan bir mal veya hizmetin tüketiminde bir marjinal çok küçük bir artışının, yani matematik notasyonla xi malının değişmesinin, toplam fayda seviyesine yaptığı etki, yani matematik notasyonla  , arasındaki bağlantıya verilen isimdir.
, arasındaki bağlantıya verilen isimdir.

Işık eğrisi, bir yıldızın veya bir bölgenin zamana karşı çizilen parlaklık grafiğidir.

Matematikte bir doğrunun eğimi ya da gradyanı o doğrunun dikliğini, eğimliliğini belirtir. Daha büyük eğim, daha dik bir doğru demektir.

Matematikte işaret kavramı, sıfırdan farklı her bir reel sayının pozitif veya negatif olduğunu belirtir. Her ne kadar bazen işaretli sıfır kullanılsa bile, sıfırın kendisi işaretsizdir. Matematik ve fizikte kullanılan reel sayıların toplamaya göre tersini ifade etmek için işaret değiştirme işlemi yapılır.
Matematikte bir fonksiyonun limiti, kalkülüs ve analizde kullanılan bir temel kavramdır ve belirli bir girişe yaklaşan bir fonksiyonun davranışı ile ilgilidir.
Fizikte, hayat çizgisi bir objenin 4 boyutlu uzayda işlediği yola denir. Objenin geçmiş mekanını her an takip etmeye de bu ad verilir. Hayat çizgisi yörüngeden ayrı bir kavramdır. Bu kavramlar zaman boyutuyla ayrılır. Ve genelde yörüngelerden daha geniş bir alanı temsil ederler, diğerlerine oranla özel göreliliğin gerçek doğasını ortaya çıkarırlar. Bu fikir Hermann Minkowski tarafından ortaya atılmıştır.Bu terim, genelde Görelilik Teorisinde kullanılır.

Lineer interpolasyon, lineer polinomlar kullanarak, verilerin bilindiği noktalardan yeni verilerin üretilmesini sağlayan bir eğri uydurma metodudur.
Eğri uydurma, muhtemelen kısıtlamalara tabi olan bir dizi veri noktasına en iyi uyan bir eğriyi veya matematiksel fonksiyonu oluşturma işlemidir. Yerleştirilen eğriler, veri görselleştirmeye yardımcı olarak, hiçbir veri bulunmadığında bir fonksiyonun değerlerini çıkarmak ve iki veya daha fazla değişken arasındaki ilişkileri özetlemek için kullanılabilir.

Yaygın kullanımda, apsis, yatay (x) ekseni ve ordinat, standart iki boyutlu bir grafiğin dikey (y) eksenini ifade eder.
Doğrusallık, grafiksel olarak düz bir çizgi olarak gösterilebilen matematiksel bir ilişkinin (fonksiyonun) özelliğidir. Doğrusallık, orantılılık kavramı ile yakından ilişkilidir. Fizikteki örnekler, bir elektrik iletkenindeki voltaj ve akımın doğrusal ilişkisini ve kütle ve ağırlık ilişkisini içermektedir. Daha karmaşık ilişkiler doğrusal olarak sayılmamaktadır.
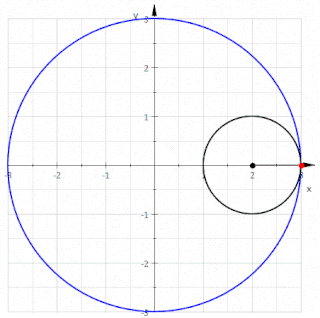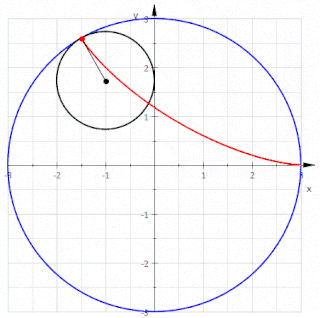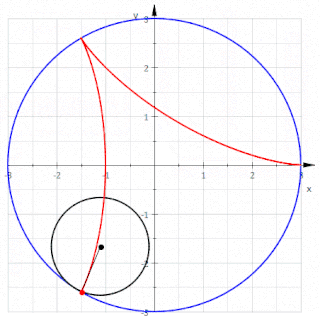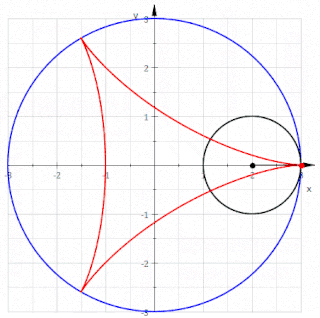
Matematikte, bir düzlem eğrisi veya düzlemsel eğri, bir düzlem içinde yer alan bir eğri olup söz konusu düzlem, bir Öklid düzlemi, bir afin düzlem veya bir projektif düzlem olabilir. En sık çalışılan durumlar, düzgün düzlem eğrileri ve cebirsel düzlem eğrisidir.











