Eylemsizlik ya da atalet, cisimlerin hareket durumlarını koruma eğilimleridir. Burada "hareket durumu" ile anlatılmak istenen, cismin diğer bir cisme göre sabit hızla hareket etmesi veya durağan halde bulunmasıdır. Maddeler için ortak özelliktir. Newton tarafından 1. hareket yasası olarak ifade edilmiştir. Bu yasa, bir cisim üzerine etkiyen dış kuvvetlerin bileşkesi sıfır olduğu zaman cismin hareket durumunun değişmeyeceğini söyler.

Türbülans veya Çalkantı bir akışkanın hareket hâlindeki düzensizliğidir. Akışkanlar dinamiğinde, türbülans veya türbülanslı akış, basınç ve akış hızında meydana gelen kaotik, stokastik değişimlerle tanımlanan bir akış rejimidir. Akışkanın düzenli katmanlar hâlinde aktığı laminer akışın aksine türbülanslı akışlar düzensiz biçimde karışarak hareket eder. Akışın hangi rejimde olduğu atalet kuvvetlerinin viskozite kuvvetlerine oranını belirten boyutsuz Reynolds sayısı ile tahmin edilebilir. Örneğin, tipik bir boru akışı için Reynolds sayısı yaklaşık 2300'ü aştıktan sonra genellikle akış, türbülanslı rejime geçer. Yüksek Reynolds sayıları türbülanslı rejimin habercisi olarak sayılabilirse de bu geçişin gerçekleştiği Reynolds sayısı birçok faktöre bağlıdır ve farklı problemlerde çok daha yüksek veya düşük bir Reynolds sayısında türbülanslı rejime geçiş olabilir.
Fizikte, kütle, Newton'un ikinci yasasından yararlanılarak tanımlandığında cismin herhangi bir kuvvet tarafından ivmelenmeye karşı gösterdiği dirençtir. Doğal olarak kütlesi olan bir cisim eylemsizliğe sahiptir. Kütleçekim kuramına göre, kütle kütleçekim etkileşmesinin büyüklüğünü de belirleyen bir çarpandır (parametredir) ve eşdeğerlik ilkesinden yola çıkılarak bir cismin kütlesi kütleçekimden elde edilebilir. Ama kütle ve ağırlık birbirinden farklı kavramlardır. Ağırlık cismin hangi cisim tarafından kütleçekime maruz kaldığına göre ve konumuna göre değişebilir.
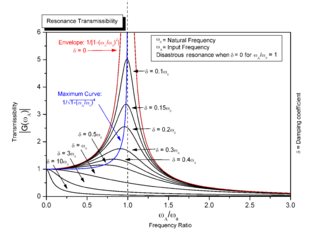
Rezonans, fizikte bir sistemin bazı frekanslarda diğerlerine nazaran daha büyük genliklerde salınması eğilimidir. Bunlar, o sistemin rezonans (tınlaşım) frekansları olarak adlandırılır. Bu frekanslarda küçük periyodik kuvvetler bile çok büyük genlikler üretebilir.

Fizikte, bir kuvvet bir cisim üzerine etki ettiğinde ve kuvvetin uygulama yönünde konum değişikliği olduğunda iş yaptığı söylenir. Örneğin, bir valizi yerden kaldırdığınızda, valiz üzerine yapılan iş kaldırıldığı yükseklik süresince ağırlığını kaldırmak için aldığı kuvvettir.

Foucault sarkacı, adını Fransız fizikçi Léon Foucault'dan alan, ilk defa deneysel olarak Dünya'nın kendi ekseni çevresinde döndüğünü kanıtlayan sarkaç düzeneği.
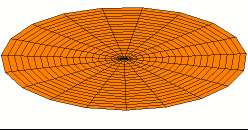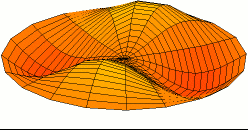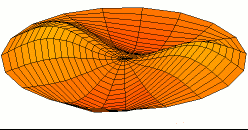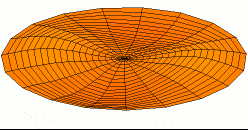
Titreşim bir denge noktası etrafındaki mekanik salınımdır. Bu salınımlar bir sarkaçın hareketi gibi periyodik olabileceği gibi çakıllı bir yolda tekerleğin hareketi gibi rastgele de olabilir.

Poisson dağılımı, olasılık kuramı ve istatistik bilim kollarında bir ayrık olasılık dağılımı olup belli bir sabit zaman birim aralığında meydana gelme sayısının olasılığını ifade eder. Bu zaman aralığında ortalama olay meydana gelme sayısının bilindiği ve herhangi bir olayla onu hemen takip eden olay arasındaki zaman farkının, önceki zaman farklarından bağımsız oluştuğu kabul edilir.

Sürekli tekdüze dağılım (İngilizce: continuous uniform distribution) olasılık kuramı ve istatistik bilim dallarında, her elemanı, olasılığın desteklendiği aynı büyüklükteki aralık içinde bulunabilir, her sürekli değer için aynı sabit olasılık gösteren bir olasılık dağılımları ailesidir. Desteklenen aralık iki parametre ile, yani minimum değer a ve maksimum değer b ile, tanımlanmaktadır. Bu dağılım kısa olarak U(a,b) olarak anılır.
Salınım, merkezi bir değere ilişkin veya iki veya daha fazla farklı durum arasındaki bazı ölçümlerin genellikle zamanla tekrarlayan veya periyodik değişimidir. Sarkaç ve alternatif akım bilinen salınım örnekleridir. Salınımlar fizikte atomlar arasındakiler gibi karmaşık etkileşimlere yaklaşmak için kullanılabilir.
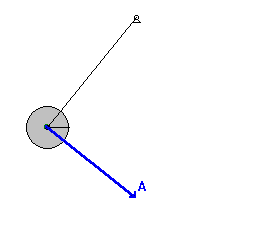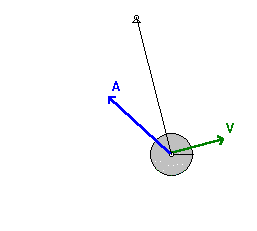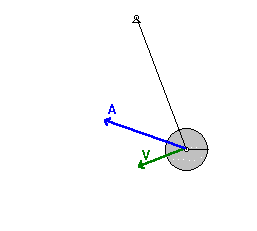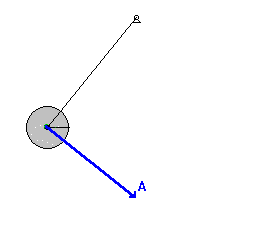
Sarkaç bir ipin bir ucuna rahatlıkla sallanabilecek şekilde bağlanılan bir kütle ile oluşturulan düzenektir. Düzenek kütleçekim kuvveti yüzünden denge konumunu muhafaza etmeye meyillidir. Kütle denge konumundan alındığında yercekimi kuvveti tarafından denge noktasina getirilmek üzere hızlandırılacak ve bu da denge noktası etrafında bir salınıma yol acar.
Spektrumun kızılötesi bölgesi, ışının 12800 ile 10 cm-1 dalga sayılı kısmını kapsar. Hem cihaz hem de uygulama açısından infrared spektrumu; yakın, orta ve uzak infrared ışınları olmak üzere üç bölgeye ayrılır. Titreşimsel spektroskopi spektrumun infrared bölgesinde oluşan moleküler titreşime bağlı olarak ışığın absorplanması ya da saçılmasını inceler. Bu incelemelerin en önemli uygulama alanları endüstriyel, zirai maddeler ve proses kontrolündeki kantitatif ve kalitatif analizlerdir. Işığın frekansı ; elektronların, rezonans frekansı civarında salınımlarına sebep olacak bir frekans değerinde olduğu vakit, genlik öylesine büyüktür ki, ortamın atomları birbirleriyle çarpışırlar ve ışık enerjisinin çoğu iç enerji halini alır ve böylece ortam tarafından emilir. Farklı maddelerin elektronları farklı rezonans frekanslarındadır. Bu ise saydam bir cisimden ya da ortamdan geçen görünür ışığı neden görebildiğinizi ve güneş yanıklarına sebep olan ultraviyole frekansların saydam bir cisimden neden geçemediklerini açıklar. bunun sonucunda, kapalı bir havada camdan bakarken güneş yanığınız olmadığı halde, açık havaya çıktığınızda güneş yanığı riskiyle karşı karşıya kalabilirsiniz.

Basit harmonik hareket, geri çağırıcı kuvvet ile doğru orantılı olarak yer değiştiren periyodik bir hareket türüdür.
Fizikte doğrusal olmayan rezonans doğrusal olmayan bir sistemde rezonansın meydana gelmesidir. Bu rezonansta sistem davranışı- rezonans frekans ve modları- salınımın genliğine bağlıdır, fakat doğrusal sistemlerde bu genlikten bağımsızdır.
Fizikte, dairesel hareket bir nesnenin dairesel bir yörünge boyunca bir rotasyon ya da çemberin çevresinde yaptığı harekettir. Rotasyonun sürekli açısal değeriyle birlikte düzgün ya da değişen rotasyon değeriyle düzensiz olabilir. 3 boyutlu bir cismin sabit ekseni etrafındaki rotasyon parçalarının dairesel hareketini içerir. Hareketin denkliği bir cisim kütlesinin merkezini tanımlar.
Birtakım dinamik denklemler, normal şartlar altında yerçekimi kuvvetinin etkisiyle hareket etmekte olan cisimlerin doğrultularını tanımlamaktadır. Örneğin; Newton'un genel yerçekimi yasası,F = mg.(m cismin kütlesi). Bu varsayım dünya yüzeyinden kısa mesafede düşmekte olan cisimler için kabul edilmesine karşın uzun mesafede serbest düşüş yapan cisimler, için tam olarak doğru değildir.

Negatif kütle, teorik fizikte normal kütlenin zıt işaretlisi olan varsayımsal madde kavramıdır, örneğin -2 kg. Bu durum bir ya da daha fazla enerji koşulunu ihlal eder ve negatif kütle için çekimin kuvvet olması gerektiği ve pozitif yönlü ivmeye sahip olması gerektiği anlaşmazlığından kaynaklanan bazı garip özellikler gösterir. Negatif kütle, solucan deliği inşa etme gibi bazı kuramsal teorilerde kullanılır. Egzotik maddeye benzeyen en yakın bilinen örnek Casimir etkisi tarafından üretilen sözde negatif basınç yoğunluğunun alanıdır. Genel izafiyet teorisinin kütleçekimini ve pozitif, negatif enerji yüklerinin hareket yasasını iyi tanımlamasına rağmen negatif kütle dolayısıyla başka temel kuvvetleri içermez. Diğer yandan, standart model, temel parçacıkları ve diğer temel kuvvetleri iyi tanımlamasına ve kütleçekimi kütle merkezini ve eylemsizliği derinlemesine içermesine rağmen kütleçekimini içermez. Negatif kütlenin kavramının daha iyi anlaşılabilmesi için kütleçekimini açık bir şekilde ifade eden modelle birlikte diğer temel kuvvetler de gerekebilir.
Medyan bir anakütle ya da örneklem veri serisini küçükten büyüğe doğru sıraladığımızda, seriyi ortadan ikiye ayıran değere denir. İstatistiğin bir alt dalı olan betimsel istatistikde medyan bir merkezsel konum ölçüsü kabul edilir.

Matematiksel istatistik, istatistiksel veri toplama tekniklerinin aksine, matematiğin bir dalı olan olasılık teorisinin istatistiğe uygulanmasıdır. Bunun için kullanılan özel matematiksel teknikler arasında matematiksel analiz, doğrusal cebir, stokastik analiz, diferansiyel denklemler ve ölçü teorisi bulunur.
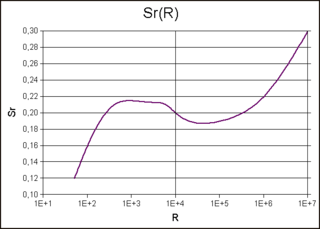
Boyut analizinde, Strouhal sayısı salınımlı akış mekanizmalarını tanımlayan bir boyutsuz sayıdır. Bu parametre, 1878 yılında vorteks saçıntısı oluşturan tellerle ve rüzgarda ses çıkaran tellerle deney yapan Çek fizikçi Vincenc Strouhal'ın adını taşır. Strouhal sayısı, akışkanlar mekaniğinin temel ilkelerinin önemli bir bileşenidir.