Doğrusal olmayan diferansiyel denlemler, doğrusal diferansiyel denklemlere yapı olarak benzemektedir. Ancak doğrusal olmayan diferansiyel denlemlerde doğrusallığı bozan terim olarak trigonometrik (
| Sınıflandırma |
| ||||||
|---|---|---|---|---|---|---|---|
| Çözümler |
| ||||||
| Uygulamalar |
| ||||||
| Matematikçiler |
| ||||||
Matematikte türev, bir fonksiyonun tanımlı olduğu herhangi bir noktada değişim yönünü veya hızını veren temel bir kavramdır. Tek değişkenli bir fonksiyonun tanım kümesinin belli bir noktasında türevi, fonksiyonun grafiğine bu noktada karşılık gelen değerde çizilen teğet doğrunun eğimidir. Teğet doğru, tanım kümesinin bu noktasında fonksiyonun en iyi doğrusal yaklaşımıdır. Bu nedenle türev genellikle anlık değişim oranı ya da daha açık bir ifadeyle, bağımlı değişkendeki anlık değişimin bağımsız değişkendeki anlık değişime oranı olarak tanımlanır. Bir fonksiyonun türevini teorik olarak bulmaya türev alma denilir. Eğer bir fonksiyonun tanım kümesindeki her değerinde hesaplanan türev değerlerini veren başka bir fonksiyon varsa, bu fonksiyona eldeki fonksiyonun türevi denir.
Matematikte, diferansiyel denklem, bir ya da birden fazla fonksiyonu ve bunların türevlerini ilişkilendiren denklemdir. Fizik, kimya, mühendislik, biyoloji ve ekonomi alanlarında matematiksel modeller genellikle diferansiyel denklemler kullanılarak ifade edilirler. Bu denklemlerde, fonksiyonlar genellikle fiziksel ya da finansal değerlere, fonksiyon türevleriyse değerlerin değişim hızlarına denk gelir.
Regresyon analizi, iki ya da daha çok nicel değişken arasındaki ilişkiyi ölçmek için kullanılan analiz metodudur. Eğer tek bir değişken kullanılarak analiz yapılıyorsa buna tek değişkenli regresyon, birden çok değişken kullanılıyorsa çok değişkenli regresyon analizi olarak isimlendirilir. Regresyon analizi ile değişkenler arasındaki ilişkinin varlığı, eğer ilişki var ise bunun gücü hakkında bilgi edinilebilir. Regresyon terimi için öz Türkçe olarak bağlanım sözcüğü kullanılması teklif edilmiş ise de Türk ekonometriciler arasında bu kullanım yaygın değildir.
Matematikte adi diferansiyel denklem, tek değişkenli fonksiyonların türevlerini ilişkilendiren diferansiyel denklem çeşididir. Adi diferansiyel denklemler adı daha yaygındır. Kapalı olarak 
Matematikte, Laplace dönüşümü, zaman tanım kümesinde tanımlı bir fonksiyonu, frekans tanım kümesinde tanımlı bir başka fonksiyona dönüştürmek amacıyla kullanılır.
Fizik, fiziksel kimya ve mühendislikte akışkanlar dinamiği, akışkanların akışını tanımlayan akışkanlar mekaniğinin bir alt disiplinidir. Aerodinamik ve hidrodinamik dahil olmak üzere çeşitli alt disiplinleri vardır. Akışkanlar dinamiğinin, uçaklardaki kuvvetlerin ve momentlerin hesaplanması, boru hatları boyunca petrolün Kütle akış hızının belirlenmesi, hava durumu modellerinin tahmin edilmesi, uzaydaki bulutsuların anlaşılması ve fisyon silahı patlamasının modellenmesi dahil olmak üzere geniş bir uygulama yelpazesi vardır.
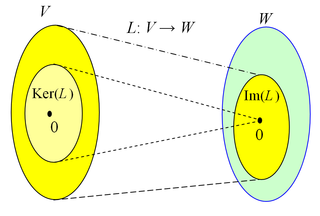
Matematikte matris veya dizey, dikdörtgen bir sayılar tablosu veya daha genel bir açıklamayla, toplanabilir veya çarpılabilir soyut miktarlar tablosudur. Dizeyler daha çok doğrusal denklemleri tanımlamak, doğrusal dönüşümlerde çarpanların takibi ve iki parametreye bağlı verilerin kaydedilmesi amacıyla kullanılırlar. Dizeylerin toplanabilir, çıkartılabilir, çarpılabilir, bölünebilir ve ayrıştırılabilir olmaları, doğrusal cebir ve dizey kuramının temel kavramı olmalarını sağlamıştır.
İndüktans elektromanyetizma ve elektronikte bir indüktörün manyetik alan içerisinde enerji depolama kapasitesidir. İndüktörler, bir devrede akımın değişimiyle orantılı olarak karşı voltaj üretirler. Bu özelliğe, onu karşılıklı indüktanstan ayırmak için, aynı zamanda öz indüksiyon da denir. Karşılıklı indüktans, bir devredeki indüklenen voltajın başka bir devredeki akımın zamana göre değişiminin etkisiyle oluşur.
Doğrusal ya da lineer denklem terimlerinin her biri ya birinci dereceden değişken ya da bir sabit olan denklemlerdir. Böyle denklemlere "doğrusal" denmesinin nedeni içerdikleri terim ve değişkenlerin sayısına bağlı olarak (n) düzlemde ya da uzayda bir doğru belirtmesindendir. Doğrusal denklemlerin en yaygını bir 
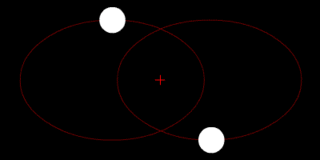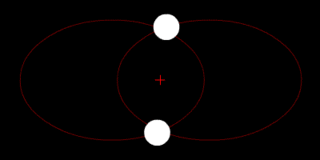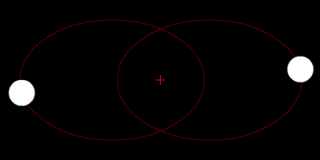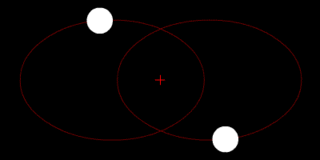
Klasik mekanikte iki cisim problemi sadece birbirleriyle etkileşen iki nokta parçacığın hareketini tanımlamak için kullanılır. Bir gezegen ve yörüngesinde dolanan bir uydu, bir yıldız ve yörüngesindeki bir gezegen, birbirlerinin yörüngelerinde dolanan iki yıldız ve klasik atom modelinde çekirdeğin etrafında dolanan elektron, yaygın örneklerdir.
Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda potansiyel teorisi olarak da bilinmektedir.
Bessel fonksiyonları ilk önce Daniel Bernoulli tarafından tanımlanmış ve Friedrich Bessel tarafından genelleştirilmiş
Doğrusal denklem dizgesi, birkaç tane aynı tip değişkenleri içeren birkaç tane doğrusal denklemlerin oluşturduğu topluluktur. Örneğin:
Matematiksel model, bir sistemin matematiksel kavramlar ve dil kullanılarak tanımlanmasıdır. Matematiksel model geliştirme süreci, matematiksel modelleme olarak adlandırılır. Matematiksel modeller, doğa bilimlerinde ve mühendislik disiplinlerinde bunun yanı sıra sosyal bilimlerde kullanılır. Matematiksel modelleri daha çok fizikçiler, mühendisler, istatistikçiler, operasyon araştırma analistleri ve ekonomistler kullanır. Model, bir sistemi açıklamaya, farklı bileşenlerin etkilerini incelemeye ve bir davranış hakkında öngörüde bulunmak için yardımcı olabilir.
Doğrusal cebirde, bir 
Diofantos denklemi diğer bir adıyla Diophantine denklemleri adını M.S. 3. yüzyılda yaşadığı tahmin edilen Antik Yunan matematikçilerden Diofantos'dan alan değişkenleri ve katsayıları tam sayılar olan denklemlerdir. Diofantos Arithmetika adlı sadece 6 cildi günümüze ulaşan çalışmasında 130 denkleme ve bunların çözümlerine yer vermiştir.
Lagrange mekaniği, klasik mekaniğin yeniden formüle edilmesidir. İtalyan-Fransız matematikçi ve astronom Joseph-Louis Lagrange tarafından 1788’de geliştirilmiştir.
Diğer bir adı sabitlerin değişimi olarak bilinir. Bu teknik homojen olmayan lineer diferansiyel denklemlerde partiküler (özel) çözümü bulmak için kullanılır.
Numerov'un yöntemi, birinci mertebeden terimin görünmediği ikinci mertebeden adi diferansiyel denklemleri çözmek için sayısal bir yöntemdir. Dördüncü dereceden doğrusal çok adımlı bir yöntemdir. Yöntem örtüktür, ancak diferansiyel denklem lineer ise açık hâle getirilebilir.
Lazarus Immanuel Fuchs, doğrusal diferansiyel denklemler alanında önemli araştırmalara katkıda bulunan Yahudi-Alman matematikçidir. Moschin (Mosina)'da doğmuş ve Berlin, Almanya'da ölmüştür. Schöneberg'de St. Matthew's Mezarlığı'na gömülmüştür. H bölümündeki mezarı korunmuş ve Berlin Eyaleti'nin şeref mezarı olarak listelenmiştir.