
Matematikte, bir polinom belirli sayıda bağımsız değişken ve sabit sayıdan oluşan bir ifadedir. Polinom kendi içinde toplama, çıkarma, çarpma ve negatif olmayan sayının üssünü alma işlemlerini kullanır. Örnek olarak tek bilinmeyenli bir polinom olan x2 − 4x + 7, ikinci dereceden oluşan bir polinomdur. Diğer bir örnek olarak, x2 − 4/x + 7x3/2 bir polinom değildir, çünkü polinomlarda terimlerin derecelerinin doğal sayı olma zorunluluğu vardır 2. terimde x′i ele alan bir bölme işlemi x'in derecesini negatif yapmaktadır ve 3. terim doğal sayı olmayan bir derece içermektedir (3/2).

Parabol, bir düzlemde alınan sabit bir "d" doğrusu ile sabit bir "F" noktasından eşit uzaklıktaki noktaların geometrik yerleştirilmesidir. Cebirde ise y=ax2+bx+c şeklindeki ikinci derece fonksiyonları grafiği olarak bilinir.
En küçük kareler yöntemi, birbirine bağlı olarak değişen iki fiziksel büyüklük arasındaki matematiksel bağlantıyı, mümkün olduğunca gerçeğe uygun bir denklem olarak yazmak için kullanılan, standart bir regresyon yöntemidir. Bir başka deyişle bu yöntem, ölçüm sonucu elde edilmiş veri noktalarına "mümkün olduğu kadar yakın" geçecek bir fonksiyon eğrisi bulmaya yarar. Gauss-Markov Teoremi'ne göre en küçük kareler yöntemi, regresyon için optimal yöntemdir.
Bir olasılık dağılımı bir rassal olayın ortaya çıkabilmesi için değerleri ve olasılıkları tanımlar. Değerler olay için mümkün olan tüm sonuçları kapsamalıdır ve olasılıkların toplamı bire eşit olmalıdır. Örneğin, bir rassal olay olarak madeni paranın tek bir defa havaya atılıp yere düşmesi ele alınsın; değerler 'yazı' veya 'tura' veya bunlar isimsel değişken ölçeğinde ifade edilirse 0 (yazı) veya 1 (tura) olur; olasılıklar ise her iki değer için ½ olacaktır. Böylece madeni bir paranın tek bir defa atılma olayı için iki değer ve ilişkili iki olasılık bu rassal olayın olasılık dağılımı olur. Bu dağılım ayrık olasılık dağılımıdır; çünkü sayılabilir şekilde ayrı ayrı sonuçlar ve bunlara bağlı olan pozitif olasılıklar vardır.

Olasılık kuramı bilim dalında bir olasılık kütle fonksiyonu bir ayrık rassal değişkenin olasılığının tıpatıp belli bir değere eşit olduğunu gösteren bir fonksiyondur. Olasılık kütle fonksiyonu, olasılık yoğunluk fonksiyonundan farklıdır; çünkü olasılık yoğunluk fonksiyonu yalnızca sürekli rassal değişkenler için tanımlanmış olup doğrudan doğruya olasılık değerini vermezler. Olasılık yoğunluk fonksiyonunun bir belli değer aralığı için integrali alınırsa bu rassal değişkenin belirlenen değer aralığı için olasılığını verir.

Doğrusal denklem dizgesi, birkaç tane aynı tip değişkenleri içeren birkaç tane doğrusal denklemlerin oluşturduğu topluluktur. Örneğin:
Matematikte, birkaç fonksiyon ya da fonksiyon gruplarının kendi isimleri yeterli öneme layıktır. Bu makaleler fonksiyonları açıklamak için olan daha ayrıntılı olarak gösteren bir listedir. İstatistik dışı ve matematiksel fizik gelişmeleri sonucu özel fonksiyonlar büyük bir teori olmuştur. Modern bir, soyut incelik fonksiyon uzayıları geniş karşılaştırma görünümü, sonsuz-boyutlu ve 'isimsiz' fonksiyonlar içindeki ve simetri ya da ilişki harmonik analiz ve grup temsilileri gibi özellikler ile özel fonksiyonlar ile seçilmiştir.

Matematikte bir doğrunun eğimi ya da gradyanı o doğrunun dikliğini, eğimliliğini belirtir. Daha büyük eğim, daha dik bir doğru demektir.

Matematikte Öklid uzayı, Öklid geometrisinin üç boyutlu uzayıdır ve bu kavramlar, çok boyutlu olarak genelleştirilir. “Öklid” terimi bu uzayları, Öklid geometrisi olmayan eğimli uzaydan ve Einstein'nın genel görelilik kuramından ayırt eder. Bu adı Yunan matematikçi Öklid'den dolayı almıştır.
Matematikte doğrusal fonksiyon, her ne kadar bu terimle ile ifade edilse bile aslında şu iki farklı terimle ilgilidir:
- Kalkülüste ve ilgili dallarında doğrusal fonksiyon, derecesi sıfır veya bir olan polinom fonksiyon veya sıfır polinomdur.
- Doğrusal cebir ve fonksiyonel analizde doğrusal fonksiyon, bir doğrusal dönüşümdür.
Matematikte, tek fonksiyon ve çift fonksiyon, aralarında simetri ilişki bulunan ve toplamaya göre tersleri olan fonksiyonlardır. Matematiksel analizin birçok alanında, özellikle kuvvet serisi ve Fourier serisinde sıkça kullanılır. Kuvvet fonksiyonunun eş kuvvetlerine göre adlandırılır ve şu şartı şağlar: Eğer n çift tam sayı ise, f(x) = xn, çift fonksiyon; n tek tam sayı ise, fonksiyon tek fonksiyondur.

Matematikte işaret kavramı, sıfırdan farklı her bir reel sayının pozitif veya negatif olduğunu belirtir. Her ne kadar bazen işaretli sıfır kullanılsa bile, sıfırın kendisi işaretsizdir. Matematik ve fizikte kullanılan reel sayıların toplamaya göre tersini ifade etmek için işaret değiştirme işlemi yapılır.

Parametre belirli bir sistemi tanımlamak veya sınıflandırmak için yardımcı olabilecek herhangi bir özellik. Parametre, sistemi tanımlarken veya performansını, durumunu değerlendirirken yararlı veya kritik olan bir sistem unsurudur.

Bézout teoremi, cebirsel geometride n değişkenli n polinomun ortak sıfırlarının sayısı ile ilgili bir ifadedir. Orijinal biçiminde teorem, genel olarak ortak sıfırların sayısının, polinomların derecelerinin çarpımına eşit olduğunu belirtir. Adını Fransız matematikçi Étienne Bézout'dan almıştır.

Simetri yalnızca geometride değil, matematiğin diğer dallarında da ortaya çıkar. Simetri bir tür değişmezliktir: matematiksel bir nesnenin bir dizi işlem veya dönüşüm altında değişmeden kaldığı özelliktir.
Doğrusallık, grafiksel olarak düz bir çizgi olarak gösterilebilen matematiksel bir ilişkinin (fonksiyonun) özelliğidir. Doğrusallık, orantılılık kavramı ile yakından ilişkilidir. Fizikteki örnekler, bir elektrik iletkenindeki voltaj ve akımın doğrusal ilişkisini ve kütle ve ağırlık ilişkisini içermektedir. Daha karmaşık ilişkiler doğrusal olarak sayılmamaktadır.
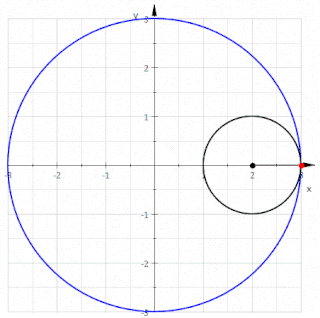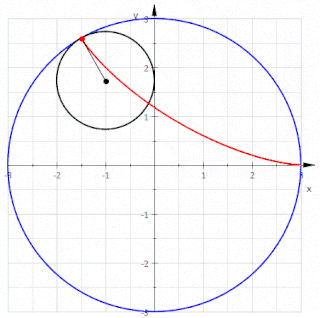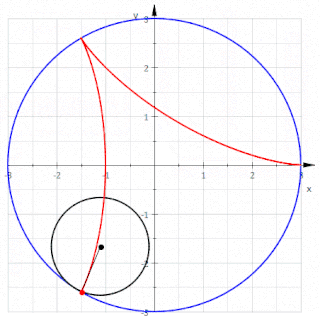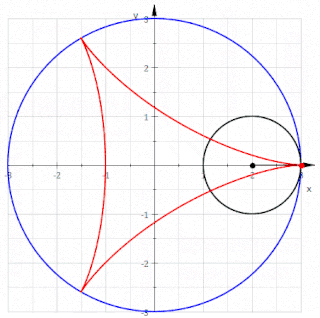
Matematikte, bir düzlem eğrisi veya düzlemsel eğri, bir düzlem içinde yer alan bir eğri olup söz konusu düzlem, bir Öklid düzlemi, bir afin düzlem veya bir projektif düzlem olabilir. En sık çalışılan durumlar, düzgün düzlem eğrileri ve cebirsel düzlem eğrisidir.




















