Dize titreşimi

Bir dizedeki (tel) titreşim bir ses dalgasıdır. Rezonans titreşen bir dizenin sabit frekanslı, yani sabit perdeli bir ses üretmesine neden olur. Telin uzunluğu veya gerginliği doğru şekilde ayarlanırsa üretilen ses bir müzik tonu olur. Titreşimli teller gitar, çello ve piyano gibi yaylı çalgıların temelini oluşturur.

Bir dizedeki dalganın yayılma hızı (b ) ipin gerilim kuvvetinin(${\displaystyle T}$ ) kare köküyle orantılıdır ve doğrusal yoğunluğun kareköküyle(${\displaystyle \mu }$ ) ters orantılıdır :

${\displaystyle v={\sqrt {T \over \mu }}.}$ Bu ilişki 1500'lerin sonlarında Vincenzo Galilei tarafından keşfedildi.^[]

Kaynak:^[1]

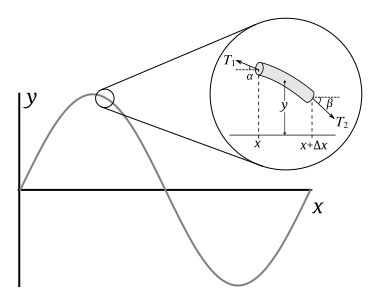
${\displaystyle \Delta x}$ bir ip parçasının uzunluğu olsun, ${\displaystyle m}$ onun kütlesi ve ${\displaystyle \mu }$ ise doğrusal yoğunluğu olsun. Eğer ${\displaystyle \alpha }$ Ve beta küçükse, her iki taraftaki gerilimin yatay bileşenlerinin her ikisi de sabit bir değerle yaklaşık olarak tahmin edilebilir. ${\displaystyle T}$ net yatay kuvvetin sıfır olduğu yer. Buna göre, küçük açı yaklaşımı kullanılarak tel parçasının her iki tarafına etki eden yatay gerilimler şu förmul ile verilmesi mümkün olanlardan sayılabilir:

${\displaystyle T_{1x}=T_{1}\cos(\alpha )\approx T.}$

${\displaystyle T_{2x}=T_{2}\cos(\beta )\approx T.}$

Newton'un dikey bileşene ilişkin ikinci yasasından, bu parçanın kütlesi (doğrusal yoğunluğunun ve uzunluğunun çarpımı olan) ivmesinin çarpımı, ${\displaystyle a}$, parça üzerindeki net kuvvete eşit olacaktır:

${\displaystyle \Sigma F_{y}=T_{1y}-T_{2y}=-T_{2}\sin(\beta )+T_{1}\sin(\alpha )=\Delta ma\approx \mu \Delta x{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Bu ifadeyi ${\displaystyle T}$ ile bölmek ve birinci ve ikinci denklemleri değiştirmek surreti ile elde ederiz (bunun için birinci veya ikinci denklem tercih edilebiliyor), böylece her birini eşleşen açıyla seçmek mümkün ${\displaystyle \beta }$ Ve ${\displaystyle \alpha }$ )

${\displaystyle -{\frac {T_{2}\sin(\beta )}{T_{2}\cos(\beta )}}+{\frac {T_{1}\sin(\alpha )}{T_{1}\cos(\alpha )}}=-\tan(\beta )+\tan(\alpha )={\frac {\mu \Delta x}{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Küçük açı yaklaşımına göre; tel parçasının uçlarındaki açıların teğetleri, uçlardaki eğimlere eşittir ve tanımından dolayı ek bir eksi işareti vardır. Bu gerçeği kullanmak ve yeniden düzenlemek şunları sağlar:

${\displaystyle {\frac {1}{\Delta x}}\left(\left.{\frac {\partial y}{\partial x}}\right|^{x+\Delta x}-\left.{\frac {\partial y}{\partial x}}\right|^{x}\right)={\frac {\mu }{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Bu sınırda ${\displaystyle \Delta x}$ sıfıra yaklaşırken sol taraf ynin ikinci türevinin tanımıdır :

${\displaystyle {\frac {\partial ^{2}y}{\partial x^{2}}}={\frac {\mu }{T}}{\frac {\partial ^{2}y}{\partial t^{2}}}.}$

Bu dalga denklemidir ${\displaystyle y(x,t)}$ ve ikinci zamana göre türev teriminin katsayısı şuna eşittir: ${\displaystyle {\frac {1}{v^{2}}}}$; Böylece

${\displaystyle v={\sqrt {T \over \mu }},}$

${\displaystyle v}$ dalganın ipteki yayılma hızıdır (bununla ilgili daha fazla bilgi için dalga denklemi hakkındaki makaleye bakın).Yatay gerilimler iyi bir şekilde tahmin edilemez. Ancak bu türetme yalnızca küçük genlikli titreşimler için geçerlidir; geniş genliğe sahip olanlar için, ${\displaystyle \Delta x}$ dize parçasının uzunluğu için iyi bir yaklaşım olmasa da gerilimin yatay bileşeni mutlaka sabit değildir.

Yayılma hızı bilindiğinde dizenin ürettiği sesin frekansı hesaplanabilir. Bir dalganın yayılma hızı dalga boyuna eşittir ${\displaystyle \lambda }$ döneme bölünür ${\displaystyle \tau }$ veya frekansla çarpılır:

${\displaystyle v={\frac {\lambda }{\tau }}=\lambda f.}$

Dizenin uzunluğu ${\displaystyle L}$ ise; temel harmonik, düğümleri dizemin iki ucu olan titreşim tarafından üretilen harmoniktir; dolayısıyla ${\displaystyle L}$ temel harmoniğin dalga boyunun yarısıdır. Buradan Mersenne kanunları elde edilir:

${\displaystyle f={\frac {v}{2L}}={1 \over 2L}{\sqrt {T \over \mu }}}$

${\displaystyle T}$ gerilimdir (Newton cinsinden), ${\displaystyle \mu }$ doğrusal yoğunluktur (yani birim uzunluk başına kütle ) ve ${\displaystyle L}$ ipin titreşen kısmının uzunluğudur . Öyleyse:

• tel ne kadar kısa olursa temelin frekansı da o kadar yüksek olur
• gerilim ne kadar yüksek olursa temel frekansın frekansı da o kadar yüksek olur
• tel ne kadar hafif olursa temel frekansın frekansı da o kadar yüksek olur

Ayrıca, n'inci harmoniği şu şekilde verilen bir dalga boyuna sahip olarak alırsak: ${\displaystyle \lambda _{n}=2L/n}$, o zaman n'inci harmoniğin frekansı için kolayca bir ifade elde ederiz:

${\displaystyle f_{n}={\frac {nv}{2L}}}$

Ve doğrusal yoğunluğa sahip T gerilimi altındaki bir ip için:

${\displaystyle f_{n}={\frac {n}{2L}}{\sqrt {\frac {T}{\mu }}}}$

Frekans yeterince düşükse ve titreşen tel televizyon veya bilgisayar (analog osiloskop değil ) gibi bir CRT ekranının önünde tutulursa, titreşen bir tel üzerindeki dalga formları görülebilir. Bu etkiye stroboskopik etki denir ve telin titreşme hızı, telin frekansı ile ekranın yenileme hızı arasındaki farktır. Aynı şey bir floresan lambada da, telin frekansı ile alternatif akımın frekansı arasındaki fark kadar bir oranda gerçekleşebilir. (Ekranın yenileme hızı telin frekansına veya tam sayı katına eşitse tel hareketsiz fakat deforme görünecektir.) Gün ışığında ve diğer salınımsız ışık kaynaklarında bu etki oluşmaz ve tel hareketsiz görünür ancak Görme kalıcılığı nedeniyle daha kalın, daha açık veya bulanık olabilecek olduğu ispata verilebildi.

Stroboskop kullanılarak benzer ancak daha kontrol edilebilir bir etki elde edilebilir. Bu cihaz, ksenon flaş lambasının frekansını telin titreşim frekansıyla eşleştirmeye olanak tanır. Karanlık bir odada bu, dalga biçimini açıkça gösterir. Aksi takdirde, aynı etkiyi elde etmek için AC frekansının aynısını veya katlarını elde etmek amacıyla bükme veya belki daha kolay bir şekilde makine kafaları ayarlanarak kullanılabilir. Örneğin, bir gitar söz konusu olduğunda, üçüncü perdeye basılan 6. (en düşük perdeli) tel 97.999'da bir G verir. Hafif bir ayarlamayla 100'e çıkarılabilir. Avrupa'da ve Afrika ve Asya'daki birçok ülkede alternatif akım frekansının tam olarak bir oktav üzerinde, 50 Hz. AC frekansının 60 olduğu Amerika kıtasının çoğu ülkesinde—beşinci teldeki A# değişitrierilerek yapılabilri, ilk perde 116,54'ten 120'ye de benzer bir etki yaratıyor.

Bir Vikipedi kullanıcısının Jackson Professional Soloist XL elektro gitarının 25⁵⁄₈ inç somun - köprü mesafesi vardır ve aşağıdaki üretici özelliklerine sahip D'Addario XL Nikel sarılı Süper hafif ölçülü EXL-120 elektro gitar telleri:

D'Addario EXL-120 üretici özellikleri

Dize numarası	Kalınlık [inç] (${\displaystyle d}$ )	Önerilen gerginlik [lbs.] (${\displaystyle T}$ )	${\displaystyle \rho }$ [g/ cm3 ]
1	0,00899	13.1	7.726 (çelik alaşımı)
2	0,0110	11.0	"
3	0,0160	14.7	"
4	0,0241	15.8	6.533 (nikel sarılı çelik alaşımı)
5	0,0322	15.8	"
6	0,0416	14.8	"

Yukarıdaki özellikler göz önüne alındığında, hesaplanan titreşim frekansları (${\displaystyle f}$ ) Yukarıdaki dizilerin temel harmonikleri, eğer teller üretici tarafından tavsiye edilen gerilimlerde dizilseydi ne olurdu?

Bunu cevaplamak için önceki bölümdeki formülle başlayabiliriz. ${\displaystyle n=1}$ :

${\displaystyle f={\frac {1}{2L}}{\sqrt {\frac {T}{\mu }}}}$

Doğrusal yoğunluk ${\displaystyle \mu }$ uzaysal (kütle/hacim) yoğunluk cinsinden ifade edilebilir ${\displaystyle \rho }$ ilişki yoluyla ${\displaystyle \mu =\pi r^{2}\rho =\pi d^{2}\rho /4}$, ${\displaystyle r}$ dizenin yarıçapıdır ve ${\displaystyle d}$ yukarıdaki tabloda çaptır (diğer adıyla kalınlık):

${\displaystyle f={\frac {1}{2L}}{\sqrt {\frac {T}{\pi d^{2}\rho /4}}}={\frac {1}{2Ld}}{\sqrt {\frac {4T}{\pi \rho }}}={\frac {1}{Ld}}{\sqrt {\frac {T}{\pi \rho }}}}$

Hesaplama amacıyla gerilimi yerine koyabiliriz ${\displaystyle T}$ yukarıda, Newton'un ikinci yasası aracılığıyla (Kuvvet = kütle × ivme), ifade ${\displaystyle T=ma}$, ${\displaystyle m}$ Dünya yüzeyinde gerilim değerlerine karşılık gelen eşdeğer ağırlığa sahip olan kütledir ${\displaystyle T}$ Yukarıdaki tabloda, Dünya yüzeyindeki yerçekimine bağlı standart ivmeyle ilişkili olarak, ${\displaystyle g_{0}=980.665}$ cm/sn ² . (Yukarıda imalatçı tarafından sağlanan ip gerilimleri kuvvet poundu cinsinden olduğundan bu ikame burada uygundur; bu, bilinen dönüştürme faktörü 1 lb. = 453,59237 g aracılığıyla en uygun şekilde kilogram cinsinden eşdeğer kütlelere dönüştürülebilir.) Yukarıdaki formül o zaman açıkça açık bir şekilde ifade edilir. olur:

${\displaystyle f_{\mathrm {Hz} }={\frac {1}{L_{\mathrm {in} }\times 2.54\ \mathrm {cm/in} \times d_{\mathrm {in} }\times 2.54\ \mathrm {cm/in} }}{\sqrt {\frac {T_{\mathrm {lb} }\times 453.59237\ \mathrm {g/lb} \times 980.665\ \mathrm {cm/s^{2}} }{\pi \times \rho _{\mathrm {g/cm^{3}} }}}}}$

F bu förmülle böyle hesaplanır::

${\displaystyle f_{1}={\frac {1}{25.625\ \mathrm {in} \times 2.54\ \mathrm {cm/in} \times 0.00899\ \mathrm {in} \times 2.54\ \mathrm {cm/in} }}{\sqrt {\frac {13.1\ \mathrm {lb} \times 453.59237\ \mathrm {g/lb} \times 980.665\ \mathrm {cm/s^{2}} }{\pi \times 7.726\ \mathrm {g/cm^{3}} }}}\approx 330\ \mathrm {Hz} }$

Bu hesaplamanın altı dizinin tümü için tekrarlanması aşağıdaki frekanslarla sonuçlanır. Her frekansın yanında, frekansı en yakın olan standart gitar akortunda müzik notası (bilimsel perde notasyonuyla ) gösterilir; bu, yukarıdaki tellerin üretici tarafından önerilen gerilimlerde dizilmesinin gerçekten de bir gitarın standart perdeleriyle sonuçlandığını doğrular:

• Perdeli aletler
• Müzikal akustik
• Dairesel bir tamburun titreşimleri
• Melde'nin deneyi
• 3. köprü (eşit tel bölünmelerine dayalı harmonik rezonans)
• Dize rezonansı
• Yansıma fazı değişimi

• Molteno, T. C. A.; N. B. Tufillaro (September 2004). "An experimental investigation into the dynamics of a string". American Journal of Physics. 72 (9): 1157-1169. doi:10.1119/1.1764557. 
• Tufillaro, N. B. (1989). "Nonlinear and chaotic string vibrations". American Journal of Physics. 57 (5): 408. doi:10.1119/1.16011. 

Özel

• Alain Goriely ve Mark Robertson-Tessi'nin yazdığı " Titreşen Tel ", Wolfram Gösterim Projesi .