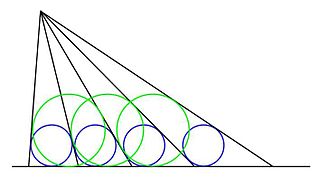
Descartes teoremi

Geometride Descartes teoremi, her dört öpüşen veya karşılıklı teğet çember için, çemberlerin yarıçaplarının belirli bir ikinci dereceden denklemi sağladığını belirtir. Bu denklemi çözerek, verilen üç karşılıklı teğet çembere teğet olan dördüncü bir çember oluşturulabilir. Teorem adını, 1643'te teoremi tanımlayan René Descartes'tan almıştır.

Teğet çemberleri içeren geometrik problemler üzerinde bin yıldır düşünülmüştür. MÖ 3. yüzyılın antik Yunanistan'ında, Pergalı Apollonius günümüze ulaşmamış olan "De tactionibus (On tangencies)" adlı bütün bir kitabı bu konuya ayırdı.

René Descartes, 1643'te Pfalz Prensesi Elisabeth'e yazdığı bir mektupta problemi kısaca tartıştı. Aşağıdaki denklem (1)'de verilenle aynı çözümü buldu ve böylece adını teoreme verdi.

Frederick Soddy, denklemi 1936'da yeniden keşfetti. Bu problemdeki öpüşen çemberler bazen Soddy çemberleri olarak da bilinir, muhtemelen Soddy teoremin kendi versiyonunu The Nature'da (20 Haziran 1936) basılan The Kiss Precise adlı bir şiir şeklinde yayınlamayı seçtiği için. Soddy ayrıca teoremi kürelere genişletti; Thorold Gosset teoremi keyfi boyutlara genişletti.

Descartes teoremi, çemberlerin eğriliği açısından en kolay şekilde ifade edilir. Bir çemberin eğriliği (veya eğimi) k= ±1/r olarak tanımlanır, burada r çemberin yarıçapıdır. Bir çember ne kadar büyükse, eğriliği o kadar küçüktür ve bunun tersi de geçerlidir.

k = ±1/r ifadesindeki artı işareti, görüntüdeki üç siyah çember gibi, diğer çemberlere dıştan teğet olan bir çembere uygulanır. Diğer çemberleri çevreleyen büyük kırmızı çember gibi içten teğet bir çember için ise eksi işareti geçerlidir.

Düz bir çizgi, sıfır eğriliği (ve dolayısıyla sonsuz yarıçapı) olan dejenere bir çember olarak kabul edilirse, Descartes teoremi, bir doğru ve üçü karşılıklı teğet olan iki çembere de uygulanır, diğer iki çembere ve çizgiye teğet olan üçüncü bir çemberin yarıçapını verir.

Dört çember altı farklı noktada birbirine teğet ise ve çemberlerin eğrilikleri k_i (i = 1, ..., 4) varsa, Descartes teoremi şöyle der:

   

${\displaystyle (k_{1}+k_{2}+k_{3}+k_{4})^{2}=2\,(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2}).}$

(1)

   Verilen üç öpüşen çembere teğet dördüncü bir çemberin yarıçapını bulmaya çalışırken, denklem en iyi şekilde şöyle yazılır:

   

${\displaystyle k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}.}$

(2)

   ± işareti, genel olarak iki çözüm olduğu gerçeğini yansıtır. Düz bir çizginin dejenere durumu göz ardı edilirse, bir çözüm pozitiftir ve diğeri pozitif veya negatiftir; negatifse, (yukarıdaki diyagramda gösterildiği gibi) ilk üçünü çevreleyen bir çemberi temsil eder.

Probleme özgü kriterler, herhangi bir problemde bir çözümü diğerine tercih edebilir.

Üç çemberden biri düz bir çizgiyle değiştirilirse, o zaman bir k_i, diyelim k₃, sıfırdır ve denklem (1) 'den elenir. Denklem (2) daha sonra çok daha basit hale gelir:

   

${\displaystyle k_{4}=k_{1}+k_{2}\pm 2{\sqrt {k_{1}k_{2}}}.}$

(3)

   İki çemberin yerini doğrular alırsa, değiştirilen iki çember arasındaki teğet, iki değiştirme doğrusu arasında bir paralellik haline gelir. Dört eğrinin hepsinin karşılıklı olarak teğet kalması için, diğer iki çemberin kesişmesi gerekir. Bu durumda k₂ = k₃ = 0 ile, denklem (2) değersiz hale gelir.

${\displaystyle \displaystyle k_{4}=k_{1}.}$

Üç doğru ve bir çemberin karşılıklı teğet olması mümkün olmadığından, üç çemberi doğrularla değiştirmek mümkün değildir. Descartes teoremi, dört çemberin tümü aynı noktada birbirine teğet olduğunda geçerli değildir.

Diğer bir özel durum, k_i'nin tam kare olduğu durumdur,

${\displaystyle (v^{2}+x^{2}+y^{2}+z^{2})^{2}=2\,(v^{4}+x^{4}+y^{4}+z^{4})}$

Euler, bunun Pisagor üçlülerinin eşzamanlı üçlüsüne eşdeğer olduğunu gösterdi.

${\displaystyle (2vx)^{2}+(2yz)^{2}=\,(v^{2}+x^{2}-y^{2}-z^{2})^{2}}$

${\displaystyle (2vy)^{2}+(2xz)^{2}=\,(v^{2}-x^{2}+y^{2}-z^{2})^{2}}$

${\displaystyle (2vz)^{2}+(2xy)^{2}=\,(v^{2}-x^{2}-y^{2}+z^{2})^{2}}$

ve parametrik bir çözüm verilebilir. Eğriliğin eksi işareti seçildiğinde,

${\displaystyle (-v^{2}+x^{2}+y^{2}+z^{2})^{2}=2\,(v^{4}+x^{4}+y^{4}+z^{4})}$

bu^[1] şu şekilde çözülebilir:

${\displaystyle {\begin{aligned}{[}&v,x,y,z]\\[6pt]={}{\Big [}&2(ab-cd)(ab+cd),\ (a^{2}+b^{2}+c^{2}+d^{2})(a^{2}-b^{2}+c^{2}-d^{2}),\\&\qquad 2(ac-bd)(a^{2}+c^{2}),\ 2(ac-bd)(b^{2}+d^{2}){\Big ]}\end{aligned}}}$

burada,

${\displaystyle a^{4}+b^{4}=\,c^{4}+d^{4}}$

olup iyi bilinen parametrik çözümlerdir.

Bir çemberi tam olarak belirlemek için, sadece yarıçapı (veya eğriliği) değil, aynı zamanda merkezi de bilinmelidir. İlgili denklem, koordinatlar (x, y) olarak gösterilmek üzere z = x + iy şeklinde karmaşık bir sayı olarak yorumlanır. Denklem daha sonra Descartes teoremine benzer görünür ve bu nedenle kompleks Descartes teoremi olarak adlandırılır.

Eğriliği k_i ve merkezleri z_i olan dört çember verildiğinde (i = 1 ... 4), denklem (1)'e ilave olarak aşağıdaki eşitlik geçerlidir:

   

${\displaystyle (k_{1}z_{1}+k_{2}z_{2}+k_{3}z_{3}+k_{4}z_{4})^{2}=2\,(k_{1}^{2}z_{1}^{2}+k_{2}^{2}z_{2}^{2}+k_{3}^{2}z_{3}^{2}+k_{4}^{2}z_{4}^{2}).}$

(4)

   Denklem (2) kullanılarak k₄ bulunduktan sonra, denklem (4), denklem (2)'ye benzer biçimde tekrar yazılarak z₄ hesaplanabilir:

${\displaystyle z_{4}={\frac {z_{1}k_{1}+z_{2}k_{2}+z_{3}k_{3}\pm 2{\sqrt {k_{1}k_{2}z_{1}z_{2}+k_{2}k_{3}z_{2}z_{3}+k_{1}k_{3}z_{1}z_{3}}}}{k_{4}}}.}$

Yine genel olarak, k₄'ün iki çözümüne karşılık gelen z₄ için iki çözüm vardır. Yukarıdaki z formülündeki artı/eksi işaretinin, k formülündeki artı/eksi işaretine karşılık gelmesi gerekmediğini unutmayın.

1886'da R. Lachlan tarafından gösterilmiş olmasına rağmen n boyuta genelleme bazen Soddy-Gosset teoremi olarak anılır. n -boyutlu Öklid uzayında, karşılıklı teğet (n−1)-kürelerin maksimum sayısı n + 2'dir. Örneğin, 3 boyutlu uzayda, beş küre karşılıklı olarak teğet olabilir. Hiper kürelerin eğrilikleri aşağıdaki eşitliği sağlar:

${\displaystyle \left(\sum _{i=1}^{n+2}k_{i}\right)^{2}=n\,\sum _{i=1}^{n+2}k_{i}^{2}}$

teoremin 2 boyutlu versiyonuna tam benzer şekilde, düz bir hiper düzleme karşılık gelen k_i = 0 durumu ile.

Karmaşık sayıların 3 boyutlu bir analojisi olmamasına rağmen, merkezlerin konumları arasındaki ilişki bir matris denklemi olarak yeniden ifade edilebilir ve bu da n boyuta genellenir.^[2]

• Ford çemberleri
• Apollon contası
• Apollonius Problemi ("çember teğetlikleri")
• Soddy altılısı
• Çemberlere teğet doğrular
• İzoperimetrik nokta

• Levrie, P. (2019), A Straightforward Proof of Descartes’s Circle Theorem. Math Intelligencer 41, ss. 24–27. https://doi.org/10.1007/s00283-019-09883-x
• Lagarias, Jeffrey & Mallows, Colin & Wilks, Allan. (2001). Beyond the Descartes Circle Theorem. The American Mathematical Monthly. 109. 10.2307/2695498.
• Jeff L’Heureux & Guthrie Scarr & Yasin Shtiui & Yang Tian. (2013). Descartes and the Apollonian Gasket, Makale 30 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• J. B. Wilker. (1969). Four Proofs of a Generalization of the Descartes Circle Theorem, The American Mathematical Monthly, 76:3, ss. 278-282, DOI: 10.1080/00029890.1969.12000194
• Mara Holloway, (2015). Generalizations and Relationships of the Descartes Circle Theorem, Makale

• Cut-the-knot'da karşılıklı olarak dört teğet çemberi gösteren etkileşimli uygulama 27 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• The Kiss Precise
• Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks: Beyond The Descartes Circle Theorem
• Descartes Circle Theorem @Wolfram MathWorld 27 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• Descartes Circle Theorem @Theorem of the day 26 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• Descartes' Circle Formula @artofproblemsolving 20 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• Soddy Circles and Descartes Theorem, Three Tangent Circles. Inscribed and Circumscribed Circles, Radii. 26 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• Descartes Complex Circle Theorem @geogebra 26 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.
• Descartes' Circle Theorem - Example and Formula 27 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi. (Video, 5:00 dk)