Matematikte, diferansiyel denklem, bir ya da birden fazla fonksiyonu ve bunların türevlerini ilişkilendiren denklemdir. Fizik, kimya, mühendislik, biyoloji ve ekonomi alanlarında matematiksel modeller genellikle diferansiyel denklemler kullanılarak ifade edilirler. Bu denklemlerde, fonksiyonlar genellikle fiziksel ya da finansal değerlere, fonksiyon türevleriyse değerlerin değişim hızlarına denk gelir.
Regresyon analizi, iki ya da daha çok nicel değişken arasındaki ilişkiyi ölçmek için kullanılan analiz metodudur. Eğer tek bir değişken kullanılarak analiz yapılıyorsa buna tek değişkenli regresyon, birden çok değişken kullanılıyorsa çok değişkenli regresyon analizi olarak isimlendirilir. Regresyon analizi ile değişkenler arasındaki ilişkinin varlığı, eğer ilişki var ise bunun gücü hakkında bilgi edinilebilir. Regresyon terimi için öz Türkçe olarak bağlanım sözcüğü kullanılması teklif edilmiş ise de Türk ekonometriciler arasında bu kullanım yaygın değildir.

Parabol, bir düzlemde alınan sabit bir "d" doğrusu ile sabit bir "F" noktasından eşit uzaklıktaki noktaların geometrik yerleştirilmesidir. Cebirde ise y=ax2+bx+c şeklindeki ikinci derece fonksiyonları grafiği olarak bilinir.
Matematikte, bir kısmi diferansiyel denklem birkaç değişkenli bir fonksiyon ile bu fonksiyonun değişkenlere göre kısmi türevleri arasındaki ilişkiyi inceler.
En küçük kareler yöntemi, birbirine bağlı olarak değişen iki fiziksel büyüklük arasındaki matematiksel bağlantıyı, mümkün olduğunca gerçeğe uygun bir denklem olarak yazmak için kullanılan, standart bir regresyon yöntemidir. Bir başka deyişle bu yöntem, ölçüm sonucu elde edilmiş veri noktalarına "mümkün olduğu kadar yakın" geçecek bir fonksiyon eğrisi bulmaya yarar. Gauss-Markov Teoremi'ne göre en küçük kareler yöntemi, regresyon için optimal yöntemdir.
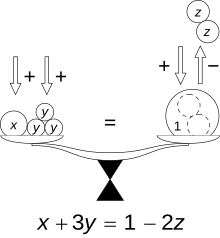
Birinci dereceden bir bilinmeyenli denklemler; a sıfırdan farklı, b ise herhangi bir gerçel veya karmaşık sayı olmak üzere,

François Viete Fransız matematikçi. Adıyla anılan Vieta formüllerini keşfetmiştir.

Matematikte Laplace denklemi, özellikleri ilk defa Pierre-Simon Laplace tarafından çalışılmış bir kısmi diferansiyel denklemdir. Laplace denkleminin çözümleri, elektromanyetizma, astronomi ve akışkanlar dinamiği gibi birçok bilim alanında önemlidir çünkü çözümler bilhassa elektrik ve yerçekim potansiyeli ile akışkan potansiyelinin davranışını açıklar. Laplace denkleminin çözümlerinin genel teorisi aynı zamanda potansiyel teorisi olarak da bilinmektedir.

Matematiksel çözümlemede Euler özdeşliği olarak adlandırılan ve Leonhard Euler tarafından bulunan eşitlik


Doğrusal denklem dizgesi, birkaç tane aynı tip değişkenleri içeren birkaç tane doğrusal denklemlerin oluşturduğu topluluktur. Örneğin:

Teğet, iki geometrik cismin, birbirlerine sadece bir noktadan temas ettiklerinde oluşan geometrik durum. İngilizcede tangent olarak anılan terimin kökeni Latince tangere (dokunuş) kelimesidir.
Sinyal (işaret), fiziksel değişkenlerin durumu hakkında bilgi taşıyan ve matematiksel olarak fonksiyon (İşlev) biçiminde gösterilen kavrama denir.
Diofantos denklemi diğer bir adıyla Diophantine denklemleri adını M.S. 3. yüzyılda yaşadığı tahmin edilen Antik Yunan matematikçilerden Diofantos'dan alan değişkenleri ve katsayıları tam sayılar olan denklemlerdir. Diofantos Arithmetika adlı sadece 6 cildi günümüze ulaşan çalışmasında 130 denkleme ve bunların çözümlerine yer vermiştir.
Matematikte Bernoulli diferansiyel denklemi, birinci mertebeden bir adi diferansiyel denklemin açık biçimi şöyledir:
 ,
,

Maxwell ilişkileri İkinci dereceden türevlerin simetri ve termodinamik potansiyellerin tanımlarından türetilebilen termodinamik denklemler dizisidir. Bu ilişkiler 19.yüzyıl fizikçisi James Clerk Maxwell tarafından adlandırılmıştır.