Debye modeli

Termodinamik ve katı hal fiziğinde Debye modeli; Peter Debye tarafından 1912 yılında geliştirilen, katılarda özgül ısıya (ısı kapasitesi) olan fonon katkısını tahmin etmek için kullanılan metottur. Atomik kristal yapının salınımlarını, bir kutu içerisindeki fononlar gibi düşünerek ele alır. Bu; katıya ayrı ayrı kuantum harmonik osilatörlerden oluşmuş olarak davranan Einstein modelinin tam tersidir. Debye modeli; ${\displaystyle }$ – Debye T³ yasası - ısı kapasitesini düşük sıcaklıklarda doğru bir şekilde tahmin eder., düşük sıcaklıklarda olan. Tıpkı Einstein modeli gibi, yüksek sıcaklıklarda Dulong–Petit Yasasını da doğru bir şekilde kapsar. Ama, ara sıcaklıklarda basitleştirmek için yapılan varsayımlar nedeniyle doğruluğu kusurludur.

Debye modelinin en doğru kullanımları için M. Sunada ve T. Sunada kaynak olarak kullanılabilir.

Debye modeli; elektromanyetik radyasyona kapalı bir kutudaki fotonlardan oluşmuş gaz olarak davranan Planck'ın siyah cisim ışımasının katı-hal muadilir. Debye modeli, atomik titreşimlere kutudaki (kutu = katı cisim) fononlar olarak yaklaşır. Hesaplamaların çoğu aynıdır.

Bir kenarı ${\displaystyle }$uzunluğunda bir küp düşünün. Kutudaki parçacık başlığında, kutunun içindeki (sadece bir eksende hizalanmış) sonik bozuklukların rezonans modlarının dalga boyları:

${\displaystyle }$

olarak verilir. ${\displaystyle }$ bir tam sayıdır. Bir fononun enerjisi ise:

${\displaystyle }$

${\displaystyle }$ Planck sabiti ve ${\displaystyle }$ bu fononun frekansıdır. Eğer frekansın dalgaboyu ile ters orantılı olduğunu varsayarsak, elimizde:

${\displaystyle }$

Burada ${\displaystyle }$ katı içindeki ses hızıdır. Üç boyutta ele alırsak:

${\displaystyle }$

${\displaystyle }$ fononun üç boyutta skaler momentum büyüklüğüdür.

Frekansın dalga boyuyla (ses hızını sabit kabul edersek) ters orantılı olduğu varsayımı yüksek-enerjili fononlar (detaylı bilgi için fonon başlığına bakınız) için olmasa da düşük-enerjili fononlar için iyi bir yaklaşımdır. Bu; Debye modelinin sınırlandırmalarından birisidir ve ara sıcaklıklarda sonuçların hatalı olmasına karşılık gelir. Oysaki düşük ve yüksek sıcaklıklarda hatasızlardır.

Şimdi kutudaki toplam enerjiyi hesaplarsak,

${\displaystyle }$

Burada ${\displaystyle }$ kutudaki ${\displaystyle }$. Diğer bir deyişle, toplam enerji, enerji ve o enerjiye sahip (tek boyutta) fonon sayısının çarpımının toplamıdır. 3 boyutta:

${\displaystyle }$

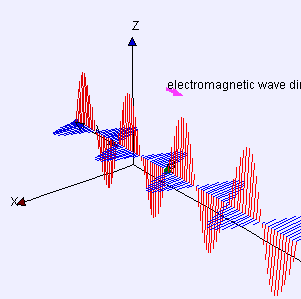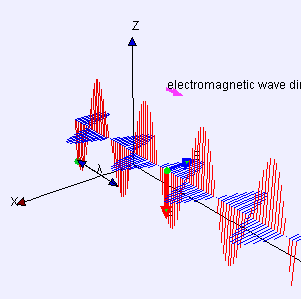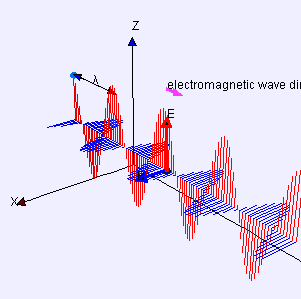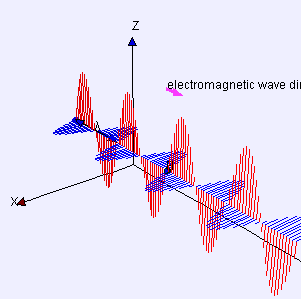
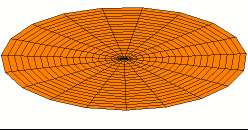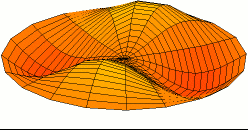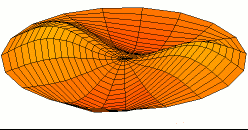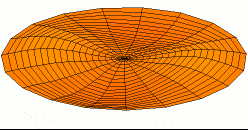
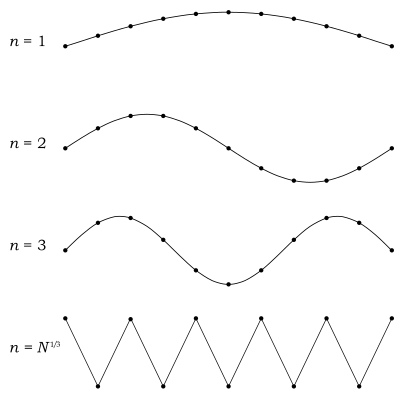
Şimdi, burası Debye modeli ve Planck'ın siyah cisim ışıması farklılaştığı yerdir. Kutudaki elektromanyetik radyasyonun aksine, fononun enerji seviyesi sayısı sınırlıdır. Çünkü, bir fonon sınırsız frekansa sahip olamaz. Frekansı, ilerlediği ortamla—katının atomik örgüsü (atomic lattice of the solid) sınırlanmıştır. Aşağıdaki; enine(transverse) bir fononun tasvirine bakınız.

Alttaki figürden de anlaşılacağı üzere, bir fononun sahip olabileceği minimum dalga boyunun atom aralığının iki katı olduğunu varsaymak makul görünüyor. Bir katının içerisinde ${\displaystyle }$ atom var. Bizim katımızın şekli bir küp, bu da demektir ki kenar başına ${\displaystyle }$ atom var. Öyleyse atom aralığı ${\displaystyle }$ve minimum dalga boyu:

${\displaystyle }$

Böylelikle; maksimum mod sayısı ${\displaystyle }$ (foton için sonsuz):

${\displaystyle }$

Bu, üçlü enerji toplamının üst sınırıdır.

${\displaystyle }$

Yavaşça değişen, sürekli (well-behaved) fonksiyonlar için, toplam integral olarak yazabilir. (Thomas-Fermi yaklaşımı):

${\displaystyle }$

Şimdiye kadar, ${\displaystyle }$${\displaystyle }$ Fononlar Bose–Einstein istatistiklerine uyarlar. Dağılımları ünlü Bose–Einstein formülü ile verilir:

${\displaystyle }$

Bir fononun üç olası kutuplaşma durumu (bir boyuna ve yaklaşık olarak enerjisini etkilemeyen iki enine) onun yukarıdaki enerji) olduğu için yukarıdaki formül 3 ile çarpılır,

${\displaystyle }$

(Aslında efektif ses hızı kullanırsak ${\displaystyle }$ Debye sıcaklığı ${\displaystyle }$ (aşağıya bakınız) ile ${\displaystyle }$daha doğrusu ${\displaystyle }$

Bunu da enerji integralinde yerine yazarsak,

${\displaystyle }$

Bu integrallerin fotonlar için hesaplanmasının kolay olmasının sebebi, ışığın frekansının, en azından yarı klasik olarak, bağlanmamış olması gerçeğidir. Yukarıdaki resimde görüldüğü gibi, bu fononlar için geçerli değildir. Debye, bu üçlü integrali yaklaşık olarak hesaplayabilmek için küresel koordinatları kullandı.

${\displaystyle }$

ve küpü, kürenin sekizde biri olarak varsaydı.

${\displaystyle }$

${\displaystyle }$ kürenin yarıçapı, küpteki ve kürenin sekizde birindeki parçacık sayının korunumu ile bulunabilir. Küpün hacmi, ${\displaystyle }$ tane birim-hücre(unit-cell) hacimi toplamına eşit.

${\displaystyle }$

Yarıçap için çözüldüğünde:

${\displaystyle }$

Doğru integral için bir küreye göre integralin yerine yazılması, modele başka bir yanlışlık kaynağı getirir.

Öyleyse enerji integrali

${\displaystyle }$

İntegral için değişken değiştirirsek ${\displaystyle }$,

${\displaystyle }$

Görünümü basitleştirmek için, Debye Sıcaklığı ${\displaystyle }$

${\displaystyle }$

Birçok referansKaynak hatası: Açılış <ref> etiketi hatalı biçimlendirilmiş veya hatalı bir ada sahip (Bkz: )Kaynak hatası: Açılış <ref> etiketi hatalı biçimlendirilmiş veya hatalı bir ada sahip (Bkz: ) Debye sıcaklığını bazı sabitler ve materyale bağlı değişkenler için kısaltma olarak tanımlar. Ancak, aşağıda gösterildiği gibi, ${\displaystyle }$ kabaca minimum dalga boyu modunun fonon enerjisine eşittir. Böylelikle Debye sıcaklığını, en yüksek frekans modunun (ve dolayısıyla her modun) uyarıldığı sıcaklık olarak yorumlayabiliriz.

Devam edersek, elimizde özgül bir iç enerji var:

${\displaystyle }$

${\displaystyle }$ : (üçüncü) Debye fonksiyonu

${\displaystyle }$ 'ye göre türevini aldığımızda, boyutsuz ısı kapasitesini elde ederiz:

${\displaystyle }$

Bu formüller, Debye modelini tüm sıcaklıklarda sağlar. Aşağıda verilen daha temel formüller, düşük ve yüksek sıcaklıkların sınırında asimptotik davranışı verir. Daha önce belirtildiği gibi, bu davranış, ara davranışa aksi olarak daha kesindir. Düşük ve yüksek enerjilerdeki kesinliğin temel nedeni, sırasıyla: (i) kesin dağılım ilişkisi (dispersion relation) ${\displaystyle }$ düşük frekanslar ve (ii) kesin seviye yoğunlukları(density of states) ${\displaystyle }$frekans aralığı başına titreşim sayısı ile ilgili olarak.

Aslında, Debye denklemini biraz daha farklı ve daha basit türetti. Sürekli ortamın katı mekaniğini kullanarak, belirli bir değerden daha düşük frekanstaki titreşim seviyesi(state) sayısının aşağıdaki ifadeye asimptotik olduğunu buldu.

${\displaystyle }$

${\displaystyle }$ hacim ve ${\displaystyle }$esneklik katsayıları ve yoğunluk ile hesaplanan bir çarpan (faktör). Bunu, T sıcaklığında bir harmonik osilatörün beklenen enerjisiyle(expected energy) birleştirirsek ve (Einstein'ın modelinde zaten kullandığı gibi) titreşim frekansları sonsuza giderse enerji:

${\displaystyle }$

Bu form düşük sıcaklıklarda doğru olan ${\displaystyle }$ davranışını verir. düşük sıcaklıklarda doğru olan davranış. Ama Debye N tane atom için ${\displaystyle }$Yaptığı varsayıma göre; bir atomik katı, titreşim seviyelerinin frekanslarının spektrumu yukarıdaki kurala uymaya devam etmek zorundaydı. Maksimum frekans ${\displaystyle }$${\displaystyle }$:

${\displaystyle }$

Debye, bu varsayımın gerçekten doğru olmadığını biliyordu (yüksek frekanslar birbirine varsayılandan daha yakındı), ancak yüksek sıcaklıktaki doğru davranışı garanti eder (Dulong-Petit yasası). Enerji şu şekildedir:

${\displaystyle }$

${\displaystyle }$

${\displaystyle }$ burada ${\displaystyle }$.'ye eşit.

${\displaystyle }$

${\displaystyle }$

${\displaystyle }$Debye fonksiyonu olarak isimlendirilen fonksiyondur.

Önce titreşim frekansı dağılımını türetiriz. Aşağıdaki türetme Appendix VI kısmından alınmıştır.Kaynak hatası: Açılış <ref> etiketi hatalı biçimlendirilmiş veya hatalı bir ada sahip (Bkz: ) Yan uzunlukları ${\displaystyle }$. Elastik dalga dalga denklemine uyacak ve düzlem dalgalardan oluşacaktır; dalga vektörü ${\displaystyle }$ ele alalım.

${\displaystyle }$

Dalga denkleminin çözümü:

${\displaystyle }$

ve sınırlayıcı şartları ${\displaystyle }$ ,${\displaystyle }$

${\displaystyle }$ pozitif tam sayılar. (2)'yi (1)'in içerisinde yerine yazarsak ve dağılım ilişkisi ${\displaystyle }$

${\displaystyle }$

Yukarıdaki denklem, sabit frekans ${\displaystyle }$${\displaystyle }$ pozitif). Frekansı ${\displaystyle }$${\displaystyle }$ (çok büyük bir paralel prizma) için elipsin hacmine yaklaşık verilebilir. Dolayısıyla, modların sayısı ${\displaystyle }$, ${\displaystyle }$ frekans aralığında:

${\displaystyle }$öylece tanımlarsak: ${\displaystyle }$.

Aşağıdaki derivasyon kaynağından alınmıştır.Kaynak hatası: Açılış <ref> etiketi hatalı biçimlendirilmiş veya hatalı bir ada sahip (Bkz: ) Titreşim frekansı ${\displaystyle }$N tane atom olduğu için, 3N tane kuantum harmonik osilatör (her x-, y-, z-, yönü için 3 tane) vardır ve ${\displaystyle }$olayısıyla ${\displaystyle }$:

   

${\displaystyle 3N=N(\nu _{D})={\frac {4\pi \nu _{D}^{3}V}{3c_{s}^{3}}}}$

(4)

.

${\displaystyle }$k: Boltzmann sabiti ve h: Planck sabiti ve (4)'ü (3)'te yerine yazdığımızda, elimizde:

;

bu tanım daha standarttır. ${\displaystyle }$.${\displaystyle }$${\displaystyle }$ Maxwell-Boltzmann istatistiklerini kullanarak, ${\displaystyle }$

${\displaystyle }$.

${\displaystyle }$

.

${\displaystyle }$ (çünkü ${\displaystyle }$ tane mod, ${\displaystyle }$. Elimizde:

${\displaystyle }$

Yukarıdaki ifadelerden 1/A için bir tanım elde edebiliriz. Bunu (6) içerisinde yazarsak:

${\displaystyle }$

${\displaystyle }$

${\displaystyle }$

Frekansa göre integral aldığımızda:

${\displaystyle }$

Eğer ${\displaystyle }$

${\displaystyle }$

Bu belirli integral tam olarak hesaplanabilir.

${\displaystyle }$

Düşük sıcaklık sınırında, yukarıda bahsedilen Debye modelinin sınırlamaları geçerli değildir ve (fononik) ısı kapasitesi, sıcaklık, elastik katsayılar ve atom başına düşen hacim arasında doğru bir ilişki verir. (bu son miktarlar, Debye sıcaklığı içerisinde bulunur)

Debye katısının sıcaklığı ${\displaystyle }$. ${\displaystyle }$ğer ${\displaystyle }$ise

${\displaystyle }$

${\displaystyle }$

Bu Dulong-Petit yasasıdır ve ısı kapasitesinin daha da yükselmesine neden olan anharmoniği dikkate almıyor olmasına rağmen oldukça doğrudur. Bir iletken veya yarıiletken katı maddenin toplam ısı kapasitesi elektronlardan da ihmal edilemez bir katkı içerebilir.

Peki Debye ve Einstein modelleri deneyle ne kadar örtüşüyor? Şaşırtıcı derecede yakın, ancak Debye düşük sıcaklıklarda doğru olmasına rağmen Einstein doğru değildir.

Modeller ne kadar farklı? Bu soruyu cevaplamak için, doğal olarak, aynı eksenlerde ikisini de çizmek gerekli. Tek sorun, çizilemeyecek olması. Hem Einstein modeli hem de Debye modeli, ısı kapasitesi için fonksiyonel bir form sağlar. Bunlar modellerdir ve ölçeksiz bir model olmaz. Ölçek, modelin gerçek dünyadaki eşdeğeri ile ilgilidir. Aşağıda verilen Einstein modelinin ölçeğini görebilirsiniz:

${\displaystyle }$

Debye modelinin ölçeği, ${\displaystyle }$

${\displaystyle }$

Bu da onları aynı eksenler dizisine koymanın mantıklı olmadığını gösterir. Bunlar aynı şeyin iki modeli fakat farklı ölçeklerde. Eğer biri Einstein'ın sıcaklığını şöyle tanımlarsa:

${\displaystyle T_{E}\ {\stackrel {\mathrm {def} }{=}}\ {\epsilon \over k}\,,}$

Öyleyse:

${\displaystyle T_{E}\neq T_{D}\,,}$

İkisini kıyaslayabilmek için, bir oran aramalıyız.

${\displaystyle {\frac {T_{E}}{T_{D}}}=?}$

Einstein katısı tek-frekanslı kuantum harmonik oscilatörden oluşur, ${\displaystyle \epsilon =\hbar \omega =h\nu }$. Bu frekans, eğer gerçekten var olsaydı, katıdaki sesin hızıyla bağlantılı olurdu. Eğer sesin ilerlemesini birbirine çarpan bir dizi atom olarak düşünürsek, atomik örgü tarafından sürdürülebilir minimum dalga boyuna ${\displaystyle \lambda _{min}}$

${\displaystyle \nu ={c_{s} \over \lambda }={c_{s}{\sqrt[{3}]{N}} \over 2L}={c_{s} \over 2}{\sqrt[{3}]{N \over V}}}$

Böylelikle Einstein sıcaklığı:

${\displaystyle T_{E}={\epsilon \over k}={h\nu \over k}={hc_{s} \over 2k}{\sqrt[{3}]{N \over V}}\,,}$

Ve aradığımız oran:

${\displaystyle {T_{E} \over T_{D}}={\sqrt[{3}]{\pi \over 6}}\ =0.805995977...}$

Şimdi her iki model de aynı grafik üzerinde çizilebilir. Bu oran, bir 3-boyutlu küre hacminin, onu içeren küpün hacmine oranının küp kökü olduğuna dikkat edelim; bu sadece yukarıdaki enerji integralini hesaplarken Debye tarafından kullanılan düzeltme faktörüdür.

Alternatif olarak, 2 sıcaklığın oranı, tüm osilatörlerin salınacağı Einstein'ın tek frekansının ve Debye'nin maksimum frekansının oranı olarak görülebilir. Einstein'ın tek frekansının Debye modeli için mevcut olan frekansların ortalaması olduğu görülebilir.

Debye modeli tamamen doğru olmasa da, diğer katkıların (oldukça mobil iletim elektronları gibi) ihmal edilebilir olduğu yalıtkan, kristal katıların düşük sıcaklık ısı kapasitesi için iyi bir yaklaşım verir. Metaller için ısıya elektron katkısı T ile orantılıdır, bu da, alçak sıcaklıklarda atomik örgü titreşimleri i${\displaystyle T^{3}}$ tarafından domine edilir. Bu durumda, Debye modeli, yalnızca belirli ısının örgü katkısı için yaklaşık olarak söylenebilir. Aşağıdaki tabloda çeşitli saf elementler için Debye sıcaklıkları listelenmiştir::

Debye modelinin deneysel verilere uyması, genellikle Debye sıcaklığının sıcaklığa bağlı olmasına izin vererek fenomenolojik olarak geliştirilir;^[1] örneğin, sıcaklık Mutlak sıfırdan yaklaşık 100 K'ye yükseldiğinde, su buzunun değeri yaklaşık 222 K'den 300 K'ye yükselir.

Diğer bozonik yarı-parçacıklar için, mesela fononlar (kuantize olmuş ses dalgaları) yerine ferromıknatıslardaki magnonlar için benzer sonuçlar kolayca elde edilebilir. Bu durumda, düşük frekanslarda farklı dağılma ilişkilerine (dispersion relation) sahiptir. Örneğin, magnonlar için ${\displaystyle E(\nu )\propto k^{2}}$ , fonon olsaydı ${\displaystyle E(\nu )\propto k}$ (dalga vektörü ${\displaystyle k=2\pi /\lambda }$). Ayrıca seviyelerin yoğunluğu farklılık gösterir. (Örneğin ${\displaystyle \int g(\nu ){\rm {d}}\nu \equiv N\,}$). Sonuç olarak ferromıknatıslarda, ısı kapasitesine magnon katkısı olur. ${\displaystyle \Delta C_{\,{\rm {V|\,magnon}}}\,\propto T^{3/2}}$, bu, yeterince düşük sıcaklıklarda fonon katkısını domine eder, ${\displaystyle \,\Delta C_{\,{\rm {V|\,phonon}}}\propto T^{3}}$. Buna karşın metallerde, düşük sıcaklıklardaki asıl ısı kapasitesine yapılan katkı ${\displaystyle \propto T}$, elektronlardan gelmektedir. Fermiyoniklerdir, ,Arnold Sommerfeld'e kadar uzanan farklı metotlarla hesaplanırlar.

Sıvılar sadece boyuna fononları destekleyebileceği, enine fononları desteklemeyeceği için, uzun bir süre boyunca, fonon teorisinin sıvıların ısı kapasitesini açıklamayacağını düşünülüyordu, katılardaki ısı kapasitesinin 2/3'ünden sorumlu olduklarını düşünürsek haksız bir çıkarım değildi. Ancak, nötronlar ve X-Işınları ile yapılan Brillouin saçılması deneyleri Yakov Frenkel'in sezgilerini destekliyordu.^[2] Bununla; her ne kadar Frenkel frekansı denilen, eşik frekansının üzerindeki frekanslarla sınırlı olsa da, enine fononların sıvılarda da mevcut olduğu anlaşıldı. Enerjinin çoğu bu yüksek-frekans modlarında bulunduğu için, basit sıvıların deneysel ısı kapasitelerine iyi bir yakınlık elde etmek için Debye modelinin basit bir modifikasyonu yeterlidir.^[3]

• Bose gas
• Debye frequency
• Gas in a box
• Kinetic theory of solids
• Grüneisen parameter

• CRC Kitabının Kimya ve Fizik, 56 Edition (1975-1976)
• Schroeder, Daniel V. Giriş için Termal Fizik. Addison-Wesley, San Francisco (2000). Bölüm 7.5.

• Özgül ısı, bir hata arama ve kullanma kuvars termal ve ısı iletkenliği deneysel olarak belirlenmesi.24 Ağustos 2018 tarihinde Wayback Machine sitesinde arşivlendi.