Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.

Matematik felsefesi, matematiğin varlıksal, bilgisel ve yöntemsel sorunlarını inceleyen, matematiğin temelleriyle ilgili ana kavramları irdeleyen bir felsefe dalıdır.

Tam sayılar, sayılar kümesinde yer alan sıfır (0), pozitif yönde yer alan doğal sayılar ve bunların negatif değerlerinden oluşan negatif sayılardan oluşan sayı kümesidir.
Kategori teorisi ya da Ulam kuramı, matematiksel yapılar ve bunlar arasındaki ilişkilerle soyut olarak ilgilenen bir matematik kuramıdır. Kategori kuramı, öğelere (nesnelere) yoğunlaşan küme kuramının aksine, nesneler arası ilişkilere (morfizmlere) odaklanır.
Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.

Bir matematikçi, genellikle matematik problemlerini çözmek için çalışmalarında kapsamlı bir matematik bilgisini kullanan kişidir. Matematikçiler sayılar, veriler, miktar, yapı, alan, modeller ve değişimle ilgilenirler.

Doğrusal cebir ya da lineer cebir; matematiğin, vektörler (yöney), vektör uzayları, doğrusal dönüşümler, doğrusal denklem takımları ve matrisleri (dizey) inceleyen alanıdır. Vektör uzayları, modern matematiğin merkezinde yer alan bir konudur. Bundan dolayı doğrusal cebir hem soyut cebirde hem de fonksiyonel analizde sıkça kullanılır. Doğrusal cebir, analitik geometri ile de alakalı olup sosyal bilimlerde ve fen bilimlerinde yaygın bir uygulama alanına sahiptir.

Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.
Matematikte, nokta çarpım, sayıl çarpım veya skaler çarpım, değer olarak iki vektör alan ve sonuç olarak skaler bir değer döndüren işleme denir.

Fizikte eşbakışım (simetri), herhangi bir gözlenebilir büyüklük düşünüldüğünde belirli dönüşümler altında sistemin bazı özelliklerin değişmeyişini anlatır. Bir fizik siteminin eşbakışımı sistemin fizik veya matematik ile ilgili gözlemlenebilir veya içsel ve bazı etkenlerin değişmesi altında değişmeyen bir özelliğini ifade eder.
Matematikte Hankel dönüşümü, diğer adıyla Fourier–Bessel dönüşümü, herhangi bir f(r) fonksiyonunu sonsuz sayıda birinci tip Bessel fonksiyonlarının Jν(kr) oranlı toplamı olarak gösterir. Bu dönüşümde ortogonal temeli oluşturan Bessel fonksiyonlarının hepsi aynı ν mertebesindedir. Bu integral dönüşümü ilk kez matematikçi Hermann Hankel tarafından tasvir edilmiştir. Formülü ve ters dönüşümü sırasıyla şu şekilde verilebilir:


Matematikte, integral geometri, belirli bir uzayın simetri grubu altındaki geometrik uzay değişmezi üzerindeki ölçü teorisidir. Daha yakın zamanlarda, anlam, bir geometrik uzaydaki fonksiyon uzayından başka bir geometrik uzaydaki fonksiyon uzayına değişmeyen dönüşümlerin bir görünümünü içerecek şekilde genişletildi. Bu tür dönüşümler genellikle Radon dönüşümü ve genellemeleri gibi integral dönüşümlerin biçimini alır.

Matematikte, dönüşüm geometrisi veya dönüşümsel geometri, geometrik dönüşüm gruplarına ve bunların içindeki değişmez özelliklere odaklanarak geometri çalışmalarına verilen matematiksel ve pedagojik yaklaşımın adıdır. Teoremleri ispatlamaya odaklanan Öklid geometrisinin klasik sentetik geometri yaklaşımına karşıdır.

Mildred Sanderson Amerikalı bir matematikçiydi ve en çok modüler değişmezlerle ilgili matematiksel teoremiyle tanınıyordu.
MathWorld, Eric W. Weisstein tarafından oluşturulan ve büyük ölçüde kendisi tarafından yazılan çevrimiçi bir matematik referans çalışmasıdır. Wolfram Research, Inc. tarafından himaye edilmiş ve ona lisanslanmıştır ve kısmen Ulusal Bilim Vakfı'nın Urbana – Champaign'deki Illinois Üniversitesi'ne verdiği Ulusal Bilim Dijital Kütüphanesi hibesi tarafından finanse edilmiştir.
Bu yazıda geometrik şekilleri analiz etmek ve işlemek için kullanılan şekil analizi türü anlatılmaktadır.

Simetri grubu, grup teorisinde nesnenin değişmez olduğu, kompozisyonun grup işlemine sahip olduğu tüm dönüşümlerin grubudur. Böyle bir dönüşüm, nesneyi kendisine alan ve nesnenin tüm ilgili yapısını koruyan ortam uzayının tersine çevrilebilir bir eşlemesidir. Bir X nesnesinin simetri grubu için sık kullanılan bir gösterim G = Sym(X) şeklindedir.
Matematikte ve daha spesifik olarak cebirsel topoloji ve çokyüzlü kombinatorikte Euler karakteristiği, nasıl olursa olsun topolojik uzayın şeklini veya yapısını tanımlayan bir sayı olan topolojik değişmezdir. Genellikle  ile gösterilir.
ile gösterilir.
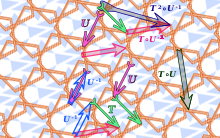
Fizikte, özellikle çokludoğrusal cebir ve tensör analizinde, kovaryans ve kontravaryans belirli geometrik veya fiziksel varlıkların nicel tanımının temelin değişmesiyle nasıl değiştiğini açıklar. Modern matematiksel gösterimde bu roller bazen yer değiştirir.