Davranış ağacı (yapay zeka, robotik ve kontrol)

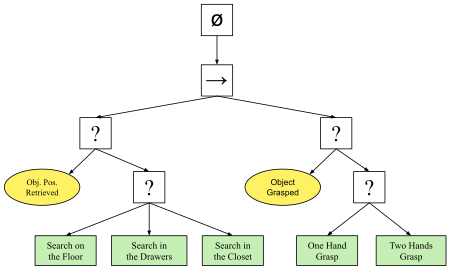
Davranış ağacı, bilgisayar bilimi, robotik, kontrol sistemleri ve video oyunlarında kullanılan matematiksel bir plan yürütme modelidir. Sonlu bir dizi görev arasındaki geçişleri modüler bir şekilde tanımlamaktadır. Güçleri, basit görevlerin nasıl uygulanacağı konusunda endişelenmeden, basit görevlerden oluşan çok karmaşık görevler oluşturma yeteneklerinden gelmektedir. Davranış ağaçları, bir davranışın ana yapı taşının bir durumdan ziyade bir görev olması arasındaki temel farkla, hiyerarşik durum makinelerine bazı benzerlikler sunmaktadır. İnsan anlayışının kolaylığı, davranış ağaçlarını daha az hataya açık hale getirmiştir. Davranış ağaçlarının diğer birkaç kontrol mimarisini genelleştirdiği gösterilmiştir.^[1][2] Matematiksel olarak yönlendirilmiş dönsüz grafiklerdir.

Davranış ağaçları, bilgisayar oyunu endüstrisinden, oyuncu olmayan karakterlerin (NPC'ler) davranışını modellemek için güçlü bir araç olarak ortaya çıkmaktadır.^[3][4][5][6] Halo, Bioshock ve Spore gibi yüksek profilli video oyunlarında yaygın olarak kullanılmıştır. Son çalışmalar, davranış ağaçlarını İHA, karmaşık robotlar, robotik manipülasyon ve çoklu robot sistemleri için çok görevli bir kontrol çerçevesi olarak önermektedir.^{[7][8][9][10][11][12]} Davranış ağaçları artık Game AI ders kitaplarında^[13][14] ve Unity (oyun motoru) ve Unreal Engine gibi genel oyun ortamlarında ele alınacak olgunluğa ulaşmıştır.

Davranış ağaçları, geliştirme paradigmaları için popüler hale gelmiştir. Sadece NPC'nin eylemlerini programlayarak ve ardından yaprak düğümleri eylemler olan ve iç düğümleri NPC'nin karar vermesini belirleyen bir ağaç yapısı (genellikle sürükle ve bırak yoluyla) tasarlayarak karmaşık bir davranış yaratabilmektedir. Davranış ağaçları görsel olarak sezgiseldir ve tasarlaması, test etmesi ve hata ayıklaması kolaydır. Diğer davranış oluşturma yöntemlerinden daha fazla modülerlik, ölçeklenebilirlik ve yeniden kullanılabilirlik sağlamaktadır.

Yıllar boyunca, davranış ağaçlarının çeşitli uygulamaları, olay güdümlü davranış ağaçlarına dönüşene kadar endüstrinin taleplerini karşılamak için hem verimlilik hem de yetenekler açısından gelişmeye devam etmiştir.^[5][15] Olay güdümlü davranış ağaçları, ağacın dahili olarak yürütmesini nasıl idare ettiğini değiştirerek ve olaylara tepki verebilen ve çalışan düğümleri iptal edebilen yeni bir düğüm türü sunarak klasik davranış ağaçlarının bazı ölçeklenebilirlik sorunlarını çözmüştür. Günümüzde, olay güdümlü davranış ağacı kavramı bir standarttır ve basitlik için hala "davranış ağaçları" olarak adlandırılsalar da, uygulamaların çoğunda kullanılmaktadır.

Bir davranış ağacı, düğümlerin kök, kontrol akış düğümleri veya yürütme düğümleri (görevler) olarak sınıflandırıldığı yönlendirilmiş bir ağaç olarak grafiksel şekilde temsil edilmektedir. Her bir bağlı düğüm çifti için giden düğüme ebeveyn, gelen düğüme alt düğüm denmektedir. Kökün ebeveyni ve tam olarak bir çocuğu(alt dalı) yoktur. Kontrol akış düğümlerinin bir ebeveyni ve en az bir çocuğu vardır. Yürütme düğümlerinin bir ebeveyni ve çocuğu yoktur. Grafiksel olarak, bir kontrol akış düğümünün çocukları, soldan sağa doğru sıralanarak onun altına yerleştirilmektedir.^[16]

Bir davranış ağacının yürütülmesi, çocuğuna belirli bir sıklıkta işaretler gönderen kökten başlamaktadır. Bir onay işareti, bir çocuğun yürütülmesine izin veren etkinleştirici bir sinyaldir. Davranış ağacında bir düğümün yürütülmesine izin verildiğinde, yürütmesi henüz bitmemişse çalışıyor, hedefine ulaşmışsa başarılı, aksi takdirde başarısızsa üst öğeye bir durum döndürmektedir.

Oluşturulduğu alt görevleri kontrol etmek için bir kontrol akış düğümü kullanılmaktadır. Bir kontrol akış düğümü, bir seçici (geri dönüş) düğümü veya bir dizi düğümü olabilmektedir. Alt görevlerinin her birini sırayla yürütmektedirler. Bir alt görev tamamlandığında ve durumunu döndürdüğünde (başarılı veya başarısız), kontrol akış düğümü bir sonraki alt görevi yürütüp yürütmemeye karar vermektedir.

Geri dönüş düğümleri, başarısız olmayan ilk çocuğu bulmak ve yürütmek için kullanılmaktadır. Bir geri dönüş düğümü, çocuklarından biri başarılı veya çalışır durumda olduğunda, başarı veya çalışıyor durum koduyla hemen geri dönmektedir. Çocuklar önem sırasına göre soldan sağa doğru işaretlenmektedir.

Kodda, bir geri dönüş kompozisyonunun algoritması şöyledir:

1 for i from 1 to n do (for i'den birer 1'er n'ye kadar do)
2     çocuk_durumu ← İşaret(çocuk(i))
3     if çocuk_durumu= çalışma
4         return çalışma
5     else if çocuk_durumu= başarı
6         return başarı
7 end
8 return başarısızlık

Dizi düğümleri, henüz başarılı olmayan ilk çocuğu bulmak ve yürütmek için kullanılmaktadır. Bir dizi düğümü, alt öğelerinden biri başarısız veya çalışır durumda olduğunda (bkz. Şekil II ve aşağıdaki kod) durum koduyla hemen geri dönmektedir. Çocuklar sırayla soldan sağa doğru işaretlenmektedir.

Kodda, bir dizi bileşimi için algoritma şöyledir:

1 for i from 1 to n do (for i'den birer 1'er n'ye kadar do)
2     çocuk_durumu ← İşaret(çocuk(i))
3     if çocuk_durumu= çalışma
4         return çalışma
5     else if çocuk_durumu= başarı
6         return başarı
7 end
8 return başarısızlık

Davranış ağaçlarının analizine kontrol teorisi araçlarını uygulamak için, üçlü grup olarak tanımlanmaktadır.^[17]

${\displaystyle T_{i}=\{f_{i},r_{i},\Delta t\},}$

• ${\displaystyle i\in \mathbb {N} }$ ağacın indeksidir.
• ${\displaystyle f_{i}:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}}$ adi fark denkleminin sağ tarafını temsil eden bir vektör alanıdır.
• ${\displaystyle \Delta t}$ bir zaman adımıdır.
• ${\displaystyle r_{i}:\mathbb {R} ^{n}\rightarrow \{R_{i},S_{i},F_{i}\}}$ iade durumudur.
• Çalışma ${\displaystyle R_{i}}$,
• Başarı ${\displaystyle S_{i}}$,
• Başarısızlık ${\displaystyle F_{i}}$ dır.

Not: Görev, ebeveyni ve çocuğu olmayan dejenere bir davranış ağacıdır.

Bir davranış ağacının yürütülmesi, aşağıdaki standart adi fark denklemleriyle tanımlanmaktadır:

${\displaystyle x_{k+t}(t_{k+1})=f_{i}(x_{k}(t_{k}))}$

${\displaystyle t_{k+1}=t_{k}+\Delta t}$

• ${\displaystyle k\in \mathbb {N} }$ ayrık zamanı temsil etmektedir.
• ${\displaystyle x\in \mathbb {R} ^{n}}$davranış ağacı tarafından modellenen sistemin durum uzayıdır.

İki karar ağacı "${\displaystyle T_{i}}$ ve ${\displaystyle T_{j}}$" bir Sıra operatörü kullanılarak daha karmaşık bir davranış ağacı ${\displaystyle T_{0}}$ olarak oluşturulabilir.

${\displaystyle T_{0}={\mbox{sıra}}(T_{i},T_{j}).}$

Ardından dönüş durumu ve ${\displaystyle T_{0}}$ ile ilişkili vektör alanı ${\displaystyle f_{0}}$ aşağıdaki gibi tanımlanmaktadır:

${\displaystyle r_{0}(x_{k})={\begin{cases}r_{j}(x_{k})&{\text{ eğer }}x_{k}\in {\mathcal {S}}_{1}\\r_{i}(x_{k})&{\text{ aksi takdirde }}.\end{cases}}}$

${\displaystyle f_{0}(x_{k})={\begin{cases}f_{j}(x_{k})&{\text{ eğer }}x_{k}\in {\mathcal {S}}_{1}\\f_{i}(x_{k})&{\text{ aksi takdirde }}.\end{cases}}}$

• Karar ağacı
• Hibrit sistem
• Kapsama mimarisi

• "ROS davranış ağacı kitaplığı". 24 Haziran 2021 tarihinde kaynağından arşivlendi. 
• "Unreal Engine 4 davranış ağacı belgeleri". 12 Kasım 2020 tarihinde kaynağından arşivlendi. 
• "AI için davranış ağaçları: Nasıl çalışırlar?". 6 Mayıs 2019 tarihinde kaynağından arşivlendi. 
• "Davranış Ağaçları: Robotunuz için Basit ama Güçlü Yapay Zeka". 25 Şubat 2020 tarihinde kaynağından arşivlendi.