Darcy Yasası

Wikimedia Commons'ta Darcy Yasası ile ilgili ortam dosyaları bulunmaktadır.

Darcy yasası ${\displaystyle Q={\frac {kA}{\mu L}}\,{\Delta p}\,}$, bir sıvının gözenekli bir ortamdan akışını tanımlayan bir denklemdir. Yasa, yer bilimlerinin bir kolu olan hidrojeolojinin temeldir. Kum yataklarından su akışı ile ilgili deneylerin sonucu.

Darcy yasası ilk olarak Fransa mühendisi Henry Darcy tarafından deneysel olarak belirlendi. Homojenleştirme yöntemleri ile Navier-Stokes denklemlerinden analitik olarak belirletebilir.^[1] Isı iletimi alanındaki Fourier yasasına, elektrik şebekeleri alanındaki Ohm yasasına ve difüzyon teorisindeki Fick yasasına benzer .

Darcy yasasının bir uygulaması bir akiferden su akışının analiz edilmesidir; Darcy yasası ve kütlenin korunumu denklemi, hidrojeolojinin temel ilişkilerinden biri olan yeraltı suyu akış denklemini basitleştirir.

Önce Morris Muskat  Darcy'nin tek (akışkan) faz denklemine viskozite ekleyerek Darcy denklemini tek fazlı bir akış için rafine etti. Bu değişiklik onu petrol endüstrisindeki araştırmacılar için uygun hale getirdi. Meslektaşları Wyckoff ve Botset'in deneysel sonuçlarına dayanarak Muskat ve Meres, Darcy yasasını petrol rezervuarının gözenekli ortamındaki çok fazlı su, yağ ve gaz akışını kapsayacak şekilde genelleştirdi. Muskat ve diğerlerinin genelleştirilmiş çok fazlı akış denklemleri, günümüze kadar var olan rezervuar mühendisliği için analitik bir temel sağlamaktadır.

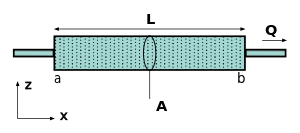
Yerçekimi kuvvetlerinin yokluğunda ve homojen olarak geçirgen bir ortamda Morris Muskat tarafından rafine edildiği gibi Darcy yasası, anlık akış hızı arasındaki basit bir orantılılık ilişkisi ile verilir. ${\displaystyle q}$ gözenekli bir ortam yoluyla geçirgenlik ${\displaystyle k}$ akışkanın, akışkanın dinamik viskozitesi ${\displaystyle \mu }$ ve basınç düşüşü ${\displaystyle \nabla p}$ belirli bir mesafede,^[2] ${\displaystyle q=-{\frac {k}{\mu }}\nabla p\,.}$

Tek fazlı (akışkan) akış için bu denklem, mutlak geçirgenlik (tek fazlı geçirgenlik) için tanımlayıcı denklemdir.^[3]

Sağdaki diyagrama atfen akı ${\displaystyle q}$ veya birim alan başına deşarj, birim olarak tanımlanır ${\displaystyle (m/s)}$, geçirgenlik ${\displaystyle k}$ birimler halinde ${\displaystyle (m^{2})}$, kesit alanı ${\displaystyle A}$ birimler halinde ${\displaystyle (m^{2})}$ toplam basınç düşüşü ${\displaystyle \Delta p=p_{b}-p_{a}}$ birimler halinde ${\displaystyle (Pa)}$, dinamik viskozite ${\displaystyle \mu }$ birimler halinde ${\displaystyle (Pa\cdot s)}$ ve ${\displaystyle L}$ numunenin birim cinsinden uzunluğu ${\displaystyle (m)}$ . Bu parametrelerin bir kısmı aşağıdaki alternatif tanımlarda kullanılmaktadır. Akışkanların yüksek basınç bölgelerinden düşük basınç bölgelerine aktığı standart fizik kuralını takiben akı tanımında negatif bir işaret kullanılır. Giriş ve çıkış farklı yüksekliklerde ise yükseklik başlığının dikkate alınması gerektiğini unutmayın. Basınçtaki değişiklik negatifse, akış pozitif x yönünde olacaktır. Mutlak geçirgenlik için kurucu bir denklem için birkaç teklif vardır ve en ünlüsü muhtemelen Kozeny denklemidir (Kozeny-Carman denklemi olarak da adlandırılır).

Darcy yasasının İntegral şekli:

${\displaystyle Q={\frac {kA}{\mu L}}\,{\Delta p}\,}$

burada Q (zaman başına hacim birimleri, örneğin ^m³ / s) toplam boşalmasıdır. Statik sıvı basıncı ilişkisini göz önünde bulundurarak (Stevin yasası ):

${\displaystyle p=\rho gh}$

kişi temsili çıkarabilir

${\displaystyle Q={\frac {kAg}{\nu L}}\,{\Delta h}\,}$

burada ν kinematik viskozitedir . Dolayısıyla karşılık gelen hidrolik iletkenlik şöyledir:

${\displaystyle K={\frac {\nu L}{kAg}}}$

Bu miktar ${\displaystyle K}$ genellikle Darcy akısı veya Darcy hızı olarak adlandırılır, sıvının gözeneklerden geçtiği hız değildir. Sıvı hızı (v ) gözeneklilik (φ) tarafından akı (q ) ile ilişkilidir ve formu alır

${\displaystyle v={\frac {q}{\varphi }}\,.}$

Darcy yasası, akiferlerde akan yeraltı suyunun sergilediği bazı tanıdık özellikleri düzgün bir şekilde özetleyen basit bir matematiksel ifadedir:

• bir mesafe boyunca basınç gradyanı yoksa, akış meydana gelmez (bunlar hidrostatik durumlardır),
• bir basınç eğimi varsa, yüksek basınçtan düşük basınca doğru akış meydana gelecektir (artan eğimin yönünün tersine - dolayısıyla Darcy yasasında negatif işaret),
• basınç eğimi ne kadar büyük olursa (aynı formasyon materyali içinden), deşarj oranı o kadar büyük olur ve
• sıvının deşarj oranı, her iki durumda da aynı basınç gradyanı mevcut olsa bile, farklı formasyon materyalleri aracılığıyla (hatta aynı materyalden farklı bir yönde) genellikle farklı olacaktır.

Bir baraj altında akan yeraltı suyu miktarını ölçmek için, kararlı durum yeraltı suyu akış denkleminin (Darcy yasası ve kütlenin korunmasına dayanan) kullanımının grafik bir gösterimi, akış ağlarının yapımındadır.

Darcy yasası sadece yavaş, viskoz akış için geçerlidir; yeraltı suyu akışı vakası bu kategoriye girmektedir. Tipik olarak Reynolds sayısı birden az olan herhangi bir akış açıkça laminerdir ve Darcy yasasının uygulanması geçerli olacaktır. Deneysel testler, 10'a kadar Reynolds sayısına sahip akış rejimlerinin, yeraltı suyu akışında olduğu gibi hala Darcian olabileceğini göstermiştir. Gözenekli ortam akışı için Reynolds sayısı (boyutsuz bir parametre) tipik olarak

${\displaystyle \mathrm {Re} ={\frac {\rho vd}{\mu }}\,,}$

burada ρ su yoğunluğu (hacim başına kütle birimi), v özgül deşarjdır (gözenek hızı değil - zaman başına uzunluk birimleriyle), d₃₀ gözenekli ortam için temsili bir tane çapıdır (standart seçim d30, elekler kullanılarak bir tane boyutu analizinden% 30 geçiş boyutu - uzunluk birimleriyle).

Sabit, sürünen, sıkıştırılamayan akış için, yani D(ρu_i)/Dt ≈ 0 için Navier Stokes denklemi basitleştirir Stokes denklemiyle kütle terimi ihmal gereğidir:

${\displaystyle \mu \nabla ^{2}u_{i}-\partial _{i}p=0\,,}$

μ viskozitesidir u_i yönünde hızı, g_i yönünde yerçekimi bileşenidir ve p basıncıdır. Viskoz direnç kuvvetinin yazabileceğimiz hız ile doğrusal olduğunu varsayarsak:

${\displaystyle -\left(k_{ij}\right)^{-1}\mu \varphi u_{j}-\partial _{i}p=0\,,}$

burada φ gözenekliliktir ve k_ij ikinci dereceden geçirgenlik tensörüdür. Bu n yönündeki hızı verir,

${\displaystyle k_{ni}\left(k_{ij}\right)^{-1}u_{j}=\delta _{nj}u_{j}=u_{n}=-{\frac {k_{ni}}{\varphi \mu }}\partial _{i}p\,,}$

Darcy'nin n yönünde hacimsel akı yoğunluğu yasasını veren,

${\displaystyle q_{n}=-{\frac {k_{ni}}{\mu }}\,\partial _{i}p\,.}$

İzotropik gözenekli ortamda geçirgenlik tensöründeki diyagonal elemanlar sıfırdır, i ≠ j için k_ij = 0 ve diyagonal elemanlar aynıdır, k_ii = k ve ortak form elde edilir

${\displaystyle {\boldsymbol {q}}=-{\frac {k}{\mu }}\,{\boldsymbol {\nabla }}p\,.}$

Yukarıdaki denklem, gözenekli bir ortamda tek fazlı sıvı akışı için geçerli bir denklemdir .

Darcy yasasının başka bir türevi, geçirgen ortamlardan akışı belirlemek için petrol mühendisliğinde yaygın olarak kullanılmaktadır - en basit olanı, tek bir sıvı fazı ve sabit sıvı viskozitesi ile tek boyutlu, homojen bir kaya oluşumu içindir.

Hemen hemen tüm yağ rezervuarlarının yağ bacağının altında bir su bölgesi vardır ve bazılarında ayrıca yağ bacağının üzerinde bir gaz kapağı bulunur. Yağ üretimi nedeniyle rezervuar basıncı düştüğünde, su aşağıdan yağ bölgesine akar ve gaz yukarıdan yağ bölgesine akar (gaz kapağı varsa) ve aynı anda tüm sıvı fazlarının karışmasını sağlarız. petrol bölgesi. Petrol sahası işletmecisi, petrol üretimini iyileştirmek için su (ve / veya gaz) da enjekte edebilir. Bu nedenle petrol endüstrisi, Muskat et alios tarafından geliştirilen çok fazlı akış için genelleştirilmiş bir Darcy denklemi kullanmaktadır. Darcy'nin adı çok yaygın ve gözenekli ortamdaki akışla güçlü bir şekilde ilişkili olduğundan, çok fazlı denklem Darcy'nin çok fazlı akış veya genelleştirilmiş Darcy denklemi (veya yasası) veya basitçe Darcy'nin denklemi (veya yasası) veya basitçe akış denklemi olarak belirtilir. metin Muskat et alios'un çok fazlı denklemini tartışıyor. Petrol ve gaz rezervuarlarında çok fazlı akış kapsamlı bir konudur ve bu konuyla ilgili birçok makaleden biri Darcy'nin çok fazlı akış yasasıdır .

Reynolds sayısı yaklaşık 1'den 10'a kadar olan gözenekli ortamlardaki akışlar için eylemsizlik etkileri de önemli olabilir. Bazen Darcy'nin Forchheimer terimi olarak bilinen denklemine ataletsel bir terim eklenir. Bu terim, basınç farkının akış verisine karşı doğrusal olmayan davranışını açıklayabilir.

${\displaystyle {\frac {\partial p}{\partial x}}=-{\frac {\mu }{k}}q-{\frac {\rho }{k_{1}}}q^{2}\,,}$

burada ilave terimi k₁ eylemsizlik geçirgenliği olarak bilinir.

Bir kumtaşı rezervuarının ortasındaki akış o kadar yavaştır ki Forchheimer denklemine genellikle ihtiyaç duyulmaz, ancak bir gaz üretim kuyusuna gaz akışı Forchheimer denkleminin kullanımını haklı çıkaracak kadar yüksek olabilir. Bu durumda, 3B modelin ızgara hücresi için değil, kuyu için giriş performansı hesaplamaları Forchheimer denklemine dayanır. Bunun etkisi, içeri akış performans formülünde ek bir hıza bağlı kaplamanın ortaya çıkmasıdır.

Bazı karbonat rezervuarlarında çok sayıda kırık vardır ve Darcy'nin çok fazlı akış denklemi, hem kırıklardaki akışı hem de matristeki akışı (yani geleneksel gözenekli kaya) yönetmek için genelleştirilir. Kırık duvarların düzensiz yüzeyi ve kırıklardaki yüksek akış hızı Forchheimer denkleminin kullanımını haklı kılabilir.

Küçük karakteristik boyutlardaki gaz akışı için (örn. Çok ince kum, nanoporöz yapılar vb.), Parçacık-duvar etkileşimleri daha sık hale gelir ve ek duvar sürtünmesine neden olur (Knudsen sürtünmesi). Hem viskoz hem de Knudsen sürtünmesinin bulunduğu bu bölgedeki bir akış için yeni bir formülasyonun kullanılması gerekir. Knudsen, küçük kılcal damarlar üzerindeki deneylerine dayanarak geçiş rejimindeki akış için yarı ampirik bir model sundu.^[4] Gözenekli bir ortam için Knudsen denklemi olarak verilebilir.

${\displaystyle N=-\left({\frac {k}{\mu }}{\frac {p_{a}+p_{b}}{2}}+D_{\mathrm {K} }^{\mathrm {eff} }\right){\frac {1}{R_{\mathrm {g} }T}}{\frac {p_{\mathrm {b} }-p_{\mathrm {a} }}{L}}\,,}$

N mol akı burada, T sıcaklığı, DeffK olup, gaz sabitidir DeffK </br> DeffK, gözenekli ortamın etkili Knudsen yayılımıdır. Model aynı zamanda ilk prensibe dayalı ikili sürtünme modelinden (BFM) türetilebilir.^[5][6] BFM'ye dayalı gözenekli ortamlarda geçiş akışının diferansiyel denklemi olarak verilmiştir.

${\displaystyle {\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}N\,.}$

Bu denklem kılcal damarlar ve gözenekli ortamlar için geçerlidir. Knudsen etkisi ve Knudsen yayılımının terminolojisi mekanik ve kimya mühendisliğinde daha yaygındır. Jeolojik ve petrokimya mühendisliğinde bu etki Klinkenberg etkisi olarak bilinir. Molar akı tanımını kullanarak, yukarıdaki denklem şu şekilde yeniden yazılabilir:

${\displaystyle {\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}{\dfrac {p}{R_{\mathrm {g} }T}}q\,.}$

Bu denklem aşağıdaki denkleme yeniden düzenlenebilir

${\displaystyle q=-{\frac {k}{\mu }}\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right){\frac {\partial p}{\partial x}}\,.}$

Bu denklemi geleneksel Darcy yasasıyla karşılaştırarak yeni bir formülasyon verilebilir.

${\displaystyle q=-{\frac {k^{\mathrm {eff} }}{\mu }}{\frac {\partial p}{\partial x}}\,,}$

nerede

${\displaystyle k^{\mathrm {eff} }=k\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right)\,.}$

Bu, Klinkenberg tarafından önerilen etkili geçirgenlik formülasyonuna eşdeğerdir:

${\displaystyle k^{\mathrm {eff} }=k\left(1+{\frac {b}{p}}\right)\,.}$

burada b, gaza ve gözenekli ortam yapısına bağlı olan Klinkenberg parametresi olarak bilinir. Yukarıdaki formülasyonları karşılaştırırsak bu oldukça belirgindir. Klinkenberg parametresi b, geçirgenliğe, Knudsen yaygınlığına ve viskozitesine (yani hem gaz hem de gözenekli ortam özelliklerine) bağlıdır.

Çok kısa zaman ölçeklerinde, Darcy yasasına çok küçük zamanlarda geçerli çözümlerle sonuçlanan bir akı zaman türevi eklenebilir (ısı transferinde buna Fourier yasasının değiştirilmiş şekli denir),

${\displaystyle \tau {\frac {\partial q}{\partial t}}+q=-k\nabla h\,,}$

burada τ, bu denklemin "normal" zamanlarda (> nanosaniye ) Darcy yasasının normal biçimine düşmesine neden olan çok küçük bir zaman sabitidir. Bunu yapmanın temel nedeni, düzenli yeraltı suyu akış denkleminin (difüzyon denklemi ) çok küçük zamanlarda sabit kafa sınırlarında tekilliklere yol açmasıdır. Bu form daha matematiksel olarak titizdir, ancak çözülmesi daha zor olan ve sadece çok küçük zamanlarda, genellikle pratik kullanım alanından yararlı olan hiperbolik bir yeraltı suyu akış denklemine yol açar.

Darcy yasasının geleneksel biçiminin bir başka uzantısı, sınırlar arasındaki geçiş akışını açıklamak için kullanılan Brinkman terimidir (Brinkman tarafından 1949'da tanıtılmıştır^[7] ),

${\displaystyle -\beta \nabla ^{2}q+q=-{\frac {k}{\mu }}\nabla p\,,}$

burada β etkili bir viskozite terimidir. Bu düzeltme terimi, ortamın tanelerinin gözenekli olduğu, ancak kullanımının zor olduğu ve tipik olarak ihmal edildiği ortamdan akışı açıklar. Örneğin, gözenekli bir hücre dışı matris matris boyunca büyük gözenekler oluşturmak için bozulursa, viskoz terim büyük gözeneklerde uygulanırken, Darcy yasası kalan bozulmamış bölgede geçerlidir. Bu senaryo teorik ve modelleme çalışmasında ele alınmıştır.^[8] Önerilen modelde, Brinkman denklemi bir dizi reaksiyon-difüzyon-konveksiyon denklemine bağlanmıştır.

Darcy yasası, tortulardan laminer akış için geçerlidir. İnce taneli sedimanlarda, aralıkların boyutları küçüktür ve bu nedenle de akış laminerdir. İri taneli çökeltiler de benzer şekilde davranırlar, ancak çok taneli çökeltilerde akış türbülanslı olabilir.^[9] Dolayısıyla Darcy yasası bu tür sedimanlarda her zaman geçerli olmaz. Dairesel borulardan akış için, Reynolds sayısı 2000'den az olduğunda akış laminer ve 4000'den fazla olduğunda türbülanslıdır, ancak bazı tortularda Reynolds sayısının değeri 1'den az olduğunda akışın laminer olduğu bulunmuştur.

• Darcy, Kaya geçirgenliği birimi
• Hidrojeoloji
• Yeraltı suyu akış denklemi
• Matematiksel model