
Topoloji, matematiğin ana dallarından biridir. Yunancada yer, yüzey veya uzay anlamına gelen topos ve bilim anlamına gelen logos sözcüklerinden türetilmiştir. Topoloji biliminin kuruluş aşamalarında yani 19. yüzyılın ortalarında, bu sözcük yerine aynı dalı ifade eden Latince analysis situs ür.

Bir üçgen düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir. Üçgene müselles ve üçbucak da denir.
Matematikte reel sayılar kümesi, Fransızca réel “gerçek” den gelmektedir. Oranlı sayılar kümesinin evrim sürecinden elde edilen bir varsayım kombinasyonudur. Reel sayılar kümesi  sembolüyle gösterilir.
sembolüyle gösterilir.
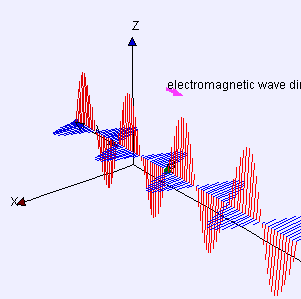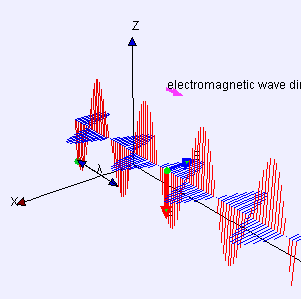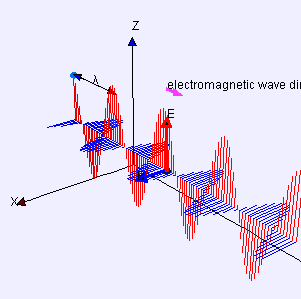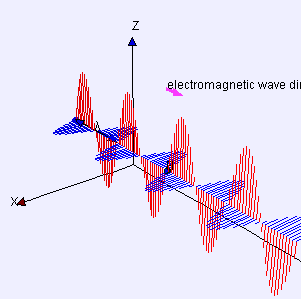
Elektromanyetik radyasyon, elektromanyetik ışınım, elektromanyetik dalga ya da elektromıknatıssal ışın bir vakum veya maddede kendi kendine yayılan dalgalar formunu alan bir olgudur. Elektromanyetik dalgalar, yüklü bir parçacığın ivmeli hareketi sonucu oluşan, birbirine dik elektrik ve manyetik alan bileşeni bulunan ve bu iki alanın oluşturduğu düzleme dik doğrultuda yayılan, yayılmaları için ortam gerekmeyen, boşlukta c ile yayılan enine dalgalardır. Elektromanyetik dalgalar, frekansına göre değişik tiplerde sınıflandırılmıştır. Bu tipler sırasıyla :
- Radyo dalgaları
- Mikrodalgalar
- Terahertz radyasyonu
- Kızılötesi ışınım
- Görünür ışık
- Morötesi ışınım
- X-ışınları ve
- Gama ışınlarıdır.

Doğru, matematikte mantıksal bir değerdir. Matematik'te ne olduğu belli olmayan (tanımsız) değerlerden biridir. Ayrıca geometride doğru ifadesi aynı doğrultuda olan ve her iki yönden de sonsuza kadar giden noktalar kümesi diye de tanımlanır. Bir doğru üzerinde en az 2 nokta, dışında da en az 1 nokta mevcuttur.

Geometride, elips bir koninin bir düzlem tarafından kesilmesi ile elde edilen düzlemsel, ikinci dereceden, kapalı eğridir.

Çember ya da dönge, düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktaların kümesinin oluşturduğu yuvarlak, geometrik şekil. Çemberin çevrelediği 2 boyutlu alana daire denir.
Hiperbolik geometri, Öklid geometrisinden bir aksiyomla ayrılır. Öklid'in paralel aksiyomunun tersini doğru olarak kabul eden geometride bir doğrunun dışındaki bir noktadan birden çok (sonsuz) tane paralel doğru geçebilir. Bunun anlamı hiperbolik geometride Öklid geometrisinin aksine herhangi bir açı oluşturmak için ışınların, doğru ve doğru parçalarının kesişmesine gerek yoktur. Bunun yerine düz olmayan tek bir doğrunun varolması yeterlidir. Ayrıca bir üçgenin iç açıları toplamı her zaman iki tane dik açıdan küçüktür.

Yıldız kümeleri veya yıldız bulutları, öz kütleçekimiyle bir arada tutulan büyük yıldız gruplarıdır. İki ana yıldız kümesi türü belirlenmiştir: Küresel kümeler, kütleçekimsel olarak bağlı on bin ila milyonlarca yaşlı yıldızın oluşturduğu sıkı gruplardır, açık kümeler ise genellikle birkaç yüzden az üye içeren, daha gevşek kümelenmiş ve çoğunlukla çok genç yıldızların oluşturduğu gruplardır. Açık kümeler, gökada içinde hareket ederken dev moleküler bulutların çekim etkisiyle zamanla dağılır, fakat küme üyeleri artık çekimsel olarak bağlı olmasalar da uzayda genel olarak aynı yönde hareket etmeye devam ederler; bunlara yıldız topluluğu, bazen de hareketli grup denir.
Vektör uzayı veya Yöney uzayı, matematikte ölçeklenebilir ve eklenebilir bir nesnelerin (vektörlerin) uzayına verilen isimdir. Daha resmî bir tanımla, bir vektör uzayı, iki elemanı arasında vektör toplamasının ve skaler denilen sayılarla çarpımın tanımlı olduğu ve bunların bazı aksiyomları sağladığı kümedir. Skalerler, rasyonal veya reel sayılar kümesinden gelebilir, ama herhangi bir cisim üzerinden bir vektör uzayı oluşturmak mümkündür. Vektör uzayları, skalerlerin geldiği cisime göre reel vektör uzayı, kompleks vektör uzayı veya genel bir cisim üzerinden K vektör uzayı şeklinde adlandırılır.

Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.

Çok katlı, topolojide soyut topolojik bir uzay. Bu uzayın her noktasının çevresi Öklit uzayına benzer. Bununla birlikte, çok katlı bir Öklit uzayı olmak zorunda değildir. Genel yapısı, bu basit yerel yapısından çok daha karmaşık olabilir. Çok katlının boyutu, yerel olarak benzediği Öklit uzayının boyutu olarak tanımlanır. Herhangi bir topolojik uzay içinse boyut kavramından söz etmek genelde olası değildir.

Sonsuz, eski Yunanca Lemniscate kelimesinden gelmektedir, çoğunlukla matematik ve fizikte herhangi bir sonu olmayan şeyleri ve sayıları tarif etmekte kullanılan soyut bir kavramdır.
Bölüm topolojisi, bir topolojik uzaydan başka bir topolojik uzay elde etmenin klasik yollarından biridir. Bir topolojik uzayda kimi noktaların birbirine yapıştırılmasıyla (özdeşleştirilmesiyle) elde edilen yeni kümenin üzerine konacak bölüm topolojisi, bu yeni kümeyi yeni bir topolojik uzaya dönüştürür. Bu yeni uzaya bölüm uzayı denir. Örneğin [0,1] kapalı aralığı bir topolojik uzaydır. Bu uzayda 0 ve 1 noktaları özdeşleştirilir ve bu yeni kümeye bölüm topolojisi verilirse oluşturulan topolojik uzay düzlemde birim çember olur. Başka bir örnek: düzlemde yatan birim yarıçaplı dairenin kenarının üst tarafındaki her bir nokta kenarın alt tarafında karşılık gelen noktaya yapıştırılır ve bu yeni kümenin üzerine bölüm topolojisi konursa, bu topolojik uzay 3 boyutlu Öklit uzayında birim yarıçaplı küre olur.

Matematikte karmaşık düzlem, gerçel eksen ve ona dik olan sanal eksen tarafından oluşturulmuş, karmaşık sayıların geometrik bir gösterimidir. Karmaşık sayının gerçel kısmının x-ekseni boyuncaki yer değiştirmeyle, sanal kısmının ise y-eksenindeki yer değiştirmeyle temsil edildiği değiştirilmiş bir Kartezyen düzlem olarak düşünülebilir.

≈
Cebirsel geometri, matematiğin bir dalıdır. Adından anlaşılabileceği gibi, soyut cebirin, özellikle değişmeli cebirin yöntemleri ile geometrinin dili ve problemlerini bir araya getirir. Çağdaş matematik içerisinde merkezi bir rol üstlenmesinin yanında, karmaşık analiz, topoloji, sayılar kuramı gibi matematiğin diğer dallarıyla yakın ilişkisi vardır.
Ayrılma belitleri bir topolojik uzayın üzerine konan ve noktaların ve altkümelerin birbirilerinden ne kadar ayrı olduğunu belirten belitler ailesi. Bir topolojik uzayın bu belitlerden birini sağladığı söylendiğinde, topolojisi hakkında global bir bilgi verilmiş ve topolojinin cinsi daraltılmış olur. Örneğin, topolojinin sahip olduğu açık kümelere bakmaksızın o topolojinin T0 olduğunu söylemek, topolojik uzayda seçilmiş herhangi iki noktanın birbirlerinden ayırt edilebilir olduğunu garanti eder.

Açık yıldız kümeleri, birkaç bin yıldızdan oluşan bir yıldız grubudur. Açık yıldız kümesini oluşturan yıldızlar aynı dev moleküler buluttan oluşmuşlardır ve yaklaşık olarak aynı yaştadırlar. Açık yıldız kümesi galaktik küme olarak da bilinir. Samanyolu Galaksisi'nde 1100'den fazla açık yıldız kümesi keşfedilmiştir ve daha fazla olduğu düşünülmektedir. Açık yıldız kümeleri karşılıklı yerçekimi etkisiyle birbirlerine gevşek bir biçimde bağlıdırlar. Açık yıldız kümeleri diğer kümelerle ve gaz bulutlarıyla yakın temaslarda bulunarak bozulmuş hale gelirler. Bu bozulmalar hem galaksinin ana bölümüne doğru yer değiştirmelere hem de küme elemanlarının yakın temasların içine doğru kaybıyla sonuçlanır.

Birebir örten fonksiyon, matematikte hem birebir hem örten fonksiyon özelliklerini aynı anda gösteren fonksiyonlardır. İki küme arasındaki fonksiyonda 1.kümeden her bir eleman ikinci kümedeki elemanla eşleşir ve her iki kümeden açıkta eleman kalmaz. Örten fonksiyon görüntü kümesinde boşta eleman kalmayacak şekilde eşleşmenin gerçekleştiği, birebir fonksiyon ise her bir elemanın diğer kümenin bir elmanıyla eşleştiği fonksiyondur. Birebir örten fonksiyonlar ise bu iki fonksiyonun özelliklerine aynı anda sahip olan fonksiyonlardır.












