Dünya'nın şekli
| Jeodezi | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||||||||
| Temelleri | ||||||||||||||||
| ||||||||||||||||
| Kavramlar | ||||||||||||||||
| ||||||||||||||||
| Teknolojiler | ||||||||||||||||
| ||||||||||||||||
| Ölçütler | ||||||||||||||||
| ||||||||||||||||
| Tarih | ||||||||||||||||
| ||||||||||||||||
Dünya'nın şekli, jeodezide, Dünya gezegenini modellemek için kullanılan kimi boyut ve şekillerdir. Şekil türü, model için gereken hassasiyet dahil olmak üzere, çoğunlukla uygulama alanına dayalı olarak farklılaşmaktadır. Küresel şekilli bir Dünya diğer birçok amaçla birlikte coğrafya ve astronomi için tatmin edici olan genel kabul görmüş tarihsel bir yaklaşımdır. Oldukça kesinliğe sahip olan kimi modeller zaman içinde geliştirilmiş olup, böylece koordinat sistemleri navigasyon, yerölçme, kadastro, arazi kullanımı ve diğer çeşitli konuların kesin ihtiyaçlarına hizmet edebilir hale gelmiştir.
Amaç
Dünyanın topoğrafik yüzeyinde, yer şekilleri ve sulak alanlarının, okyanusların çeşitliliği belirgindir. Bu topoğrafik yüzey genellikle jeofizikçilerin, hidrografların ve topoğrafların çalışma alanını oluşturmaktadır. Dünyaya ilişkin ölçümlerin yapıldığı belirgin bir yüzeyin var olmasına rağmen, düzensizlikleri dikkate alarak bunu matematiksel olarak modellemek son derece karmaşıktır.
Pisagorcu küresel Dünya kavramı, matematiksel olarak ele alınması kolay olan sade bir yüzey imkanı sunmaktadır. Birçok astronomik ve navigasyon hesaplamaları, Dünya'ya oldukça benzer bir model olan küre şeklini kullanır. Ancak, tamamen lokal olanın ötesindeki ölçeklerde mesafeleri ve alanları ölçmek için daha hassas bir şekle ihtiyaç duyulmaktadır. Tüm yüzeyin basık bir sferoid olarak modellenmesi, geoide en yakın küresel harmoniklerin kullanılması ya da bir bölgenin en uygun referans elipsoidi ile modellenmesi yoluyla daha iyi yaklaşımlar elde edilebilir.
Küçük alanların araştırılması sürecinde, yerel topoğrafyanın küresel eğriliği baskılaması nedeniyle Dünya'nın yüzeyinin düzlemsel bir modelinin kullanılması yeterli olmaktadır. Düzlem masası araştırmaları tüm Dünya'nın boyutu ve şekli göz önüne alınmaksızın göreceli olarak daha küçük alanlar için yapılmaktadır. Örneğin, belirli bir alanın veya bir kentin araştırması bu yöntem kullanılarak gerçekleştirilir.
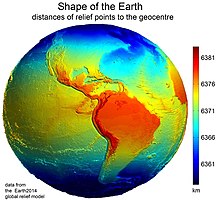
1600'lü yılların sonlarında, Dünya'yı elipsoit şeklinde olacak biçimde modelleyebilmek için Jean Picard'ın Paris meridyeni boyunca, bir yay derecesi ölçümü ile başlayan çok ciddi çabalar gösterilmiştir. Gelişen haritalar, mesafelerin daha kesin hesaplamaları ve ulusal egemenlik alanları bu erken dönem çabalarını teşvik etmiştir. Araçlarda ve teknik araştırmalardaki gelişmeler takip eden yüzyıllarda da sürmüştür. Dünyanın şeklinin modelleri bu aşamada gelişmiştir.
20. yüzyılın ortalarında, yer bilimleri araştırmaları Dünya'nın şeklinin kesin olarak tespit edilmesinde ciddi gelişmelere katkı sağlamıştır. İlk başta bu gelişmiş kesinlik durumundan elde edilen fayda balistik füzelerin eylemsizlik yönlendirme sistemleri için coğrafi ve yerçekimsel verilerini sağlamak hususunda ortay çıkmıştır. Bu durum finansman, aynı zamanda yerbilimsel disiplinlerin birçok üniversitenin yerbilim bölümlerinin oluşturulması veya genişletilmesinin teşvik edilmesiyle hızlanmıştır.[1] Bu gelişmeler, Dünya'nın şeklinin kesin modelleri olmaksızın uygulamaya alınamayacak hava durumu, iletişim uydu kontrolü ve GPS yer tespit sistemi gibi birçok sivil uğraşa da fayda sağlamıştır.
Modeller
Bir sferoid birbirinden farklı iki mesafe ölçüsüyle tanımlanır ve oluşturulur. Jeodezide bu iki hesaplamayı ifade etmek için çeşitli kurallar kullanılmaktadır, ancak bunların hepsi birbirine eşdeğerdir ve birbirine dönüştürülebilir:
Küresel

Tüm Dünya'nın şeklini yansıtan en basit model küredir. Dünya'nın yarıçapı, Dünya'nın merkezinden yüzeyine olan yaklaşık 6.371 km (3.959 mi) mesafedir. "Yarıçap" normalde mükemmel kürelerin bir özelliği olsa da, Dünya küreselden sadece yüzde üç oranında sapma gösterir, bu da onu birçok bağlamda bir küre olarak ele almak ve "Dünya'nın yarıçapı" terimini haklı çıkarmak için yeterince uygundur.
Küresel dünya konsepti M.Ö. 6. yüzyıl dönemine kadar geriye götürülebilir[2] ancak bu konsept M.Ö. 3. yüzyıla dek filozofik varsayımın bir öğesi olarak kalmıştır. Dünyanın yarıçapının ilk bilimsel tahmini Eratosthenes tarafından M.Ö. 240 yılı civarında %-1 ila %15 aralığındaki hata payı ile yapılmıştır.
Dünyanın küreselliği yaklaşık olarak kabul edilmektedir, bu nedenle tek bir değer doğal yarıçapı olarak kabul edilmemektedir. Yüzeydeki noktaların herhangi birinden merkeze olan mesafeler 6,353 km (3,948 mi) ila 6,384 km (3,967 mi) arasında değişmektedir. Dünya'yı küre olarak modellemenin birkaç farklı yolunun her biri ortalama 6.371 km (3.959 mi) mesafelik bir yarıçap hesaplar. Modelden bağımsız olarak, herhangi bir yarıçap, yaklaşık 6,357 km (3,950 mi) olan kutupsal minimum ve ekvatoral maksimum mesafenin 6,378 km (3,963 mi) arasında bir değere isabet eder. 21 km (13 mi)'lik fark kutup yarıçapının ekvator yarıçapından yaklaşık %0,3 daha kısa olmasına karşılık gelir.
Devinim elipsoidi


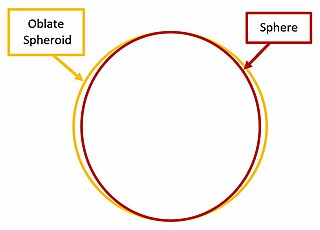
Dünya kutuplarda basık, yassılaşmış ve Ekvator'da şişkin olduğundan, jeodezi Dünya'nın şeklini basık bir sferoid olarak tanımlamaktadır. Basık sferoid ya da basık elipsoid, bir elipsin kısa ekseni etrafında döndürülmesiyle elde edilen bir devinim elipsoididir. Bu, yerkürenin şekil yapısına en çok uyan düzenli geometrik şekildir. Dünya'nın veya başka bir gök cisminin şeklini tanımlayan bir sferoide referans elipsoidi denir. Dünya için referans elipsoidine Dünya elipsoidi denir.
Dünyanın şekline ilişkin modeller kullanım alanlarına, karmaşıklığına, büyüklük ve biçimsel olarak kesinliğine göre çeşitlilik arz etmektedir.
- Ekvator yarıçapı (yarı büyük eksen olarak adlandırılır) ve kutup yarıçapı (yarı küçük eksen olarak adlandırılır);
- ve eksantriklik ;
- ve düzleştirme .
Dış merkezlik ve düzleşme, elipsoidin ne kadar basık olduğunu ifade etmenin iki farklı yoludur. Düzleşme jeodezide tanımlayıcı niceliklerden biri olarak ortaya çıktığında ise genellikle birbirinin tersiyle ifade edilirler. Örneğin günümüz GPS sistemlerinde kullanılan WGS 84 sferoidinde düzleşmenin tersi tam olarak 298.257223563 olarak ayarlanmıştır.
Dünya için bir küre ile bir referans elipsoidi arasındaki fark 300'de bir fark olmak üzere oldukça azdır. Geçmişte düzleşme yay mesafesi ölçümlerinden hesaplanmaktayken, günümüzde jeodezik ağlar ve uydu jeodezisi bu hesaplamalarda tercih edilmektedir. Uygulamada, yüzyıllar boyunca yapılan farklı araştırmalar sonucunda birçok referans elipsoidi geliştirilmiştir. Düzleştirme değeri, bir referans elipsoidinden diğerine küçük miktarda farklılaşır; bu farklılık, yerel koşulları ve referans elipsoidinin Dünya'nın tamamını mı yoksa yalnızca bir kısmını mı modellemesinin amaçlandığına göre değişmektedir.
Bir kürenin tek bir eğrilik yarıçapı vardır; bu değer yalnızca bir kürenin yarıçapıdır. Daha karmaşık yüzeyler, yüzeye göre değişen eğrilik yarıçaplarına sahiptir. Eğrilik yarıçapı, hesaplanan noktadadan yüzeye maksimum mesafede yaklaşan yarıçapı ölçüsünü tanımlar. Basık elipsoidler, yüzeyde bir ızgara çizilmesi halinde paraleller boyunca doğudan batıya sabit bir eğrilik yarıçapına sahiptir, ancak bu eğrilik diğer başka herhangi bir yönde değişir. Basık bir elipsoid için eğriliğin kutupsal yarıçapı ekvatordan daha büyüktür.
bunun nedeni kutupların düzleşmiş olmasıdır. Yüzey ne kadar düz olursa, ona yaklaşabilmek için kürenin bir o kadar büyük olması gerekir. Tersine, elipsoidin ekvatordaki kuzey-güney eğrilik yarıçapı kutuplardan daha küçüktür.
bu formülde elipsoidin merkezinden ekvator'a (yarı büyük eksen) olan mesafe; ise merkezden kutup noktasına olan mesafedir. (yarı küçük eksen)
Geoit


Yukarıda, yapılan ölçümlerin Dünya'nın görünür veya topografik yüzeyine göre yapıldığı belirtilmiş ve hesaplamaların modellenmiş bir elipsoid üzerinde yapıldığı açıklanmıştı. Ancak Jeodezik ölçümler arasında başka bir yüzey daha yer almaktadır. Geoit; Jeodezik araştırmada, noktaların jeodezik koordinatlarının hesaplanması genellikle, araştırma alanındaki Dünya'nın boyutuna ve şekline yakın bir şekilde yaklaşan bir referans elipsoidi üzerinde gerçekleştirilir. Bununla birlikte, Dünya yüzeyinde belirli aletlerle yapılan gerçek ölçümlere geoit adı verilmektedir. Elipsoid, belirli boyutlara sahip, matematiksel olarak tanımlanmış düzenli bir yüzeydir. Öte yandan geoit, Dünya'nın kütle çekimi (yerçekimi ) ve Dünya'nın dönüşünün merkezkaç kuvvetinin birleşik etkisine uyum sağlayabilmesi halinde, okyanuslar Dünyanın şekline uyumlu olarak belirlenen diğer bir yüzeyle örüşmektedir. Dünya'nın kütlesinin eşit olmayan dağılımının bir sonucu olarak, geoit yüzeyi düzensizdir. Diğer taraftan elipsoid ise düzenli bir yüzey olduğundan, ikisi arasındaki, geoit ondülasyonları, geoit yükseklikleri veya geoit ayrımları olarak adlandırılan ayrımlar aşağıdaki gibi düzensiz olacaktır:
geoit, yerçekimi potansiyelinin her yerde eşit olduğu ve yerçekimi yönünün her zaman dik olduğu bir yüzeydir (eşpotansiyel yüzeye bakınız). İkincisi, yerçekimi referanslı tesviye cihazlarını içeren optik aletler, jeodezik ölçümler yapmak için yaygın olarak kullanılır ki bu oldukça önemlidir. Düzgün ayarlandığında, aletin dikey ekseni yerçekimi yönü ile çakışır ve dolayısıyla geoite dik bir konumda bulunmuş olur. geoite dik olan çekül çizgisi (bazen "dikey" olarak da adlandırılır) ile elipsoide dik olan çizgi (bazen "elipsoidal normal" olarak da adlandırılır) arasındaki açı, düşey sapması olarak tanımlanmaktadır. Bu tanımın doğu-batı ve kuzey-güney olmak üzere iki bileşeni bulunmaktadır.[3]
Diğer şekiller
Modern jeodezi, dönüş elipsoidini bir referans elipsoidi olarak hesaplamalarda kullanma ve muhafaza etme eğilimindedir. Söz konusu bu üç eksenlilik ve armut şekli, geoit şeklinin bir parçası olarak ele alınır. Bunlar küresel harmonik katsayılarla temsil edilir. Ve , sırasıyla üç eksenlilik için 2,2 ve armut şekli için 3,0 derece ve sıra numaralarına karşılık gelir.
Üç eksenlilik (ekvator eksantrikliği)
Ekvatorun daire yerine elips olarak tanımlanması ve dolayısıyla elipsoidin üç eksenli olması olasılığı uzun yıllardır bilimsel bir tartışma konusu olmuştur.[4][5] Modern teknolojik gelişmeler, veri toplama konusunda yeni ve daha hızlı yöntemler sağlamıştır. Sputnik 1'in fırlatılmasından bu yana eliptiklik teorisini araştırmak için yörünge verileri kullanılmıştır.[3] Daha yeni sonuçlara göre ise iki büyük ekvator ve küçük atalet ekseni arasında 70 m fark bulunmakta olup; daha büyük olan yarı çap, 15° Batı boylamına (ve ayrıca 180 derece uzağa) işaret etmektedir.[6][7]
Armut şekli
Hafif armut biçimli bir Dünya teorisi, ilk yapay uyduların Güney Kutbu'nda bir çöküntüye ve Kuzey Kutbu'nda aynı derecede bir şişkinliğe işaret eden uzun periyodik yörünge değişimlerinin gözlemlemesinden sonra ortaya çıkmış ve popülerlik kazanmıştır. Bu teori, kuzeydeki orta enlemlerin hafifçe düzleştiğini, güneydeki orta enlemlerin ise buna bağlı olarak şişkin olduğunu öne sürmektedir.[3] 1958 yılı ABD yapımı Vanguard 1 adlı uydunun verilerine göre, güney ekvator çıkıntısının kuzeydekinden daha büyük olduğunu doğrulanmış ve bu durum Güney Kutbu'nun deniz seviyesinin kuzeydekinden daha düşük olmasıyla da desteklenmiştir.[8] Armut biçimli bir Dünya ilk kez 1498'de Christopher Columbus tarafından, Kuzey Yıldızı'nın günlük hareketi hakkındaki yanlış okumalarına dayanılarak kavramsallaştırılmıştır.[9]
John A. O'Keefe ve diğer yazarlar, Vanguard 1 adlı uydu verilerini kullanarak Dünya'nın çekim alanında önemli bir üçüncü derece bölgesel küresel harmonik olduğunu keşfetmişlerdir.[10] Desmond King-Hele, daha fazla uydu jeodezisi verisine dayanarak, Kuzey Kutbunda 19 m'lik bir "gövde" yükselmesi ve Güney Kutbunda 26 m'lik bir çöküntü nedeniyle kuzey ve güney kutup yarıçapları arasında 45 m'lik bir fark olduğu tahminini geliştirmiştir.[11][12] Kutup asimetrisi yine de oldukça azdır: Dünya'nın düzleşmesinden yaklaşık bin kat daha küçüktür ve Dünya'nın bazı bölgelerindeki jeoidal dalgalanmadan bile daha ufaktır.[13]
Yerel yaklaşımlar
Daha basitleştirilmiş yerel yaklaşımlar mümkündür.
Yerel teğet düzlem
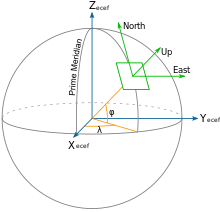
Yerel teğet düzlemi çok küçük mesafeler için uygundur.
Öskülatör küre
Belirli bir nokta civarında elipsoide en yakın yerel küresel yaklaşım Dünya'nın salınım küresidir. Yarıçapı Dünya'nın Gauss eğrilik yarıçapına eşittir ve radyal yönü jeodezik normal yönü ile çakışır. Salınım küresinin merkezi elipsoidin merkezinden kaymıştır, ancak elipsoid yüzeyinde verilen nokta için eğrilik merkezindedir. Bu kavram, karasal ve gezegensel radyo okültasyon kırılma ölçümlerinin yorumlanmasına ve bazı navigasyon ve gözetleme uygulamalarına yardımcı olur.[14][15]

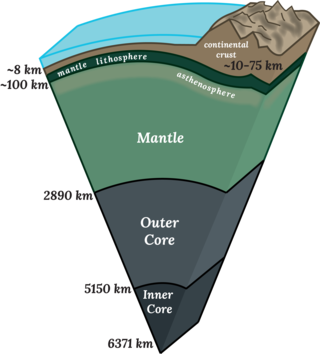
Dünyanın dönüşü ve Dünyanın iç yapısı
Dünya'nın tam şeklini belirlemek sadece jeodezinin geometrik bir görevi değil, aynı zamanda jeofiziksel hususları da içermektedir. Isaac Newton, Leonhard Euler ve diğerlerinin teorik argümanlarına göre, Dünya gibi dönen 5515 kg/m3 tekdüze yoğunluğa sahip bir cisim 1:229'luk bir düzleşmeye sahip olmalıdır. Bu sonuca, Dünya'nın iç bileşimi hakkında herhangi bir bilgi olmadan varılabilir.[16] Ancak, ölçülen yassılaşma 1:298.25'tir, bu da bir küreye daha yakındır ve Dünya'nın çekirdeğinin son derece kompakt olduğuna dair güçlü bir argümandır. Bu nedenle yoğunluk, yüzeyde 2600 kg/m3 (granit vb. kaya yoğunluğu) ile iç çekirdekte 13 000 kg/m3 arasında değişen derinliğin bir fonksiyonu olmalıdır.[17]
Küresel ve bölgesel yerçekimi alanı
Ayrıca Dünya'nın iç kısmının fiziksel keşfi için etkileri olan yerçekimi alanı, yerçekimi (kütle çekimi nedeniyle) ve merkezkaç kuvvetinin (dönme nedeniyle) net etkisidir. Bu alan yüzeyde ve uydular tarafından uzaktan çok hassas bir şekilde ölçülebilir. Topografya ve tüm jeolojik kütleler yerçekimi alanını bozduğu için gerçek dikey genellikle teorik dikey ile uyuşmaz (sapma 50" kadar değişir). Bu nedenle, yerkabuğu ve mantonun kaba yapısı yeraltının jeodezik-jeofizik modelleri ile belirlenebilir.
Ayrıca bakınız
- Clairaut teoremi
- EGM96
- Dünyanın Yerçekimi
- Horizon §§ Distance and Curvature
- Meridyen yayı
- Teorik yerçekimi
- Tarih
- Pierre Bouguer
- Dünyanın çevresi#Tarih
- Dünyanın yarıçapı#Tarih
- Düz Dünya
- Friedrich Robert Helmert
- Jeodezi tarihi
- Metrenin tarihi
- Meridyen yayı#Tarih
- Saniye sarkaç
Kaynakça
- ^ Cloud, John (2000). "Crossing the Olentangy River: The Figure of the Earth and the Military-Industrial-Academic Complex, 1947–1972". Studies in History and Philosophy of Modern Physics. 31 (3). ss. 371-404. Bibcode:2000SHPMP..31..371C. doi:10.1016/S1355-2198(00)00017-4.
- ^ Dicks, D.R. (1970). Early Greek Astronomy to Aristotle. Ithaca, N.Y.: Cornell University Press. ss. 72-198. ISBN 978-0-8014-0561-7.
- ^ a b c Defense Mapping Agency (1983). Geodesy for the Layman. United States Air Force. 28 Ağustos 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Mart 2024.
- ^ Heiskanen, W. A. (1962). "Is the Earth a triaxial ellipsoid?". Journal of Geophysical Research. 67 (1): 321-327. doi:10.1029/JZ067i001p00321.
- ^ Burša, Milan (1993). "Parameters of the Earth's tri-axial level ellipsoid". Studia Geophysica et Geodaetica. 37 (1): 1-13. doi:10.1007/BF01613918.
- ^ Torge & Müller (2012) Geodesy, De Gruyter, p. 100
- ^ Marchenko, A.N. (2009): Current estimation of the Earth’s mechanical and geometrical para meters. In Sideris, M.G., ed. (2009): Observing our changing Earth. IAG Symp. Proceed. 133., pp. 473–481. DOI:10.1007/978-3-540-85426-5_57
- ^ Tyson, Neil deGrasse (2014) [2007]. Death By Black Hole: And Other Cosmic Quandaries. 1st. New York: W. W. Norton. s. 52. ISBN 978-0-393-06224-3. OCLC 70265574.
- ^ Morison, Samuel Eliot (1991) [1942]. Admiral of the Ocean Sea: A Life of Christopher Columbus. Boston: Little, Brown and Company. s. 557. ISBN 978-0-316-58478-4. OCLC 1154365097.
- ^ O’KEEFE, J. A., ECKEIS, A., & SQUIRES, R. K. (1959). Vanguard Measurements Give Pear-Shaped Component of Earth’s Figure. Science, 129(3348), 565–566. doi:10.1126/science.129.3348.565
- ^ KING-HELE, D. G.; COOK, G. E. (1973). "Refining the Earth's Pear Shape". Nature. Springer Nature. 246 (5428): 86-88. doi:10.1038/246086a0. ISSN 0028-0836.
- ^ King-Hele, D. (1967). The Shape of the Earth. Scientific American, 217(4), 67-80.
- ^ Günter Seeber (2008), Satellite Geodesy, Walter de Gruyter, 608 pages.
- ^ Williams, Paul; Last, David (November 3–7, 2003). On Loran-C Time-Difference to Co-ordinate Converters (PDF). International Loran Association (ILA) – 32nd Annual Convention and Technical Symposium; https://loran.org/proceedings/Meeting2003/ProceedingsIndex.htm. Boulder, Colorado. CiteSeerX 10.1.1.594.6212 $2. 13 Ağustos 2023 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 5 Mart 2024.
- ^ Razin, Sheldon (Sonbahar 1967). "Explicit (Noniterative) Loran Solution". Navigation: Journal of the Institute of Navigation. 14 (3). ss. 265-269. doi:10.1002/j.2161-4296.1967.tb02208.x.
- ^ Heine, George (2013). "Euler and the Flattening of the Earth". Math Horizons. 21 (1). Mathematical Association of America. ss. 25-29. doi:10.4169/mathhorizons.21.1.25.
- ^ Dziewonski, A. M.; Anderson, D. L. (1981), "Preliminary reference Earth model" (PDF), Physics of the Earth and Planetary Interiors, 25 (4), ss. 297-356, Bibcode:1981PEPI...25..297D, doi:10.1016/0031-9201(81)90046-7, ISSN 0031-9201, 30 Temmuz 2020 tarihinde kaynağından arşivlendi (PDF), erişim tarihi: 5 Mart 2024
- İlişkilendirme
![]() Bu madde bu kaynaktan gelen kamu malı içermektedir: Defense Mapping Agency (1983). Geodesy for the Layman. United States Air Force.
Bu madde bu kaynaktan gelen kamu malı içermektedir: Defense Mapping Agency (1983). Geodesy for the Layman. United States Air Force.
İlave okuma
- Guy Bomford, Geodesy, Oxford 1952 and 1980.
- Guy Bomford, Determination of the European geoit by means of vertical deflections. Rpt of Comm. 14, IUGG 10th Gen. Ass., Rome 1954.
- Karl Ledersteger and Gottfried Gerstbach, Die horizontale Isostasie / Das isostatische geoit 31. Ordnung. Geowissenschaftliche Mitteilungen Band 5, TU Wien 1975.
- Helmut Moritz and Bernhard Hofmann, Physical Geodesy. Springer, Wien & New York 2005.
- Geodesy for the Layman, Defense Mapping Agency, St. Louis, 1983.