Kare, murabba veya dördül, bütün kenarları ve açıları birbirine eşit olan düzgün dörtgendir. Matematiğin en temel geometrik şekillerinden biridir. Bir kare aynı zamanda dikdörtgen ve eşkenar dörtgendir. Bu iki özel dörtgenin tüm özelliklerini taşır. Eski adı ise murabbadır.
Çokgen, düzlemde herhangi ardışık üçü doğrusal olmayan n tane noktayı ikişer ikişer birleştiren doğru parçalarının oluşturduğu kapalı şekillerdir.
Dikdörtgen, karşılıklı kenarları birbirine eşit, dik ve paralel olan dörtgene denir.
Paralelkenar, karşılıklı kenarları eşit olan ve iç açıları toplamı 360 derece olan bir dörtgendir. Karşılıklı kenarları paralel ve uzunlukları eşittir.
Kare aşağıdaki anlamlara gelebilir:
- Kare, geometride bütün kenarları ve açıları eşit olan dörtgen
- Kare alma, matematikte bir sayının kendisiyle çarpılması işlemi
- Kare ya da film karesi, bir filmin görsel kısmını oluşturan pek çok fotoğraftan biri
Matematikte bir döşeme, aralarında boşluk bırakmadan veya örtüşmeden bir düzlemi kaplayan düzlemsel şekiller kümesidir. Bu kavram daha yüksek boyutlar için de genellenebilir, bu genişletilmiş anlamı için döşeme yerine tesselasyon terimi kullanılır. Tesselasyon M. C. Escher'in eserlerinde sıkça görülebilir. Tesselasyona sanat tarihi boyunca, antik mimariden modern sanata kadar rastlanabilir.
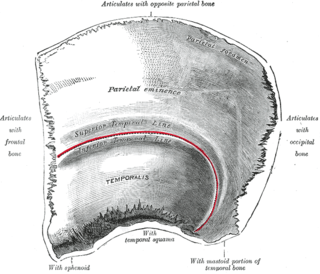
Paryetal kemik kafatası'nın kenarlarının ve çatısının birleştiği kemiktir. Her kemik düzensiz dörtgen biçimindedir ve iki yüzeyi, dört kenarı ve dört açısı vardır. İsmi Latince pariet-(duvar)'dan gelir.
Girih karoları, İslam sanatında görülen girih desenlerini oluşturmak için kullanılan, beş tip karodur. Karoların üzerinde bulunan çizgiler, karolar belli biçimlerde döşendiğinde yıldızlar, çokgenler ve karmaşık biçimde birbirini kesen şerit desenleri meydana gelir. Bu desenlerin örnekleri binalarda, kitap kapaklarında ve halılarda görülen bir süslemedir.
Matematiğin bir alt dalı olan Geometride bir eşkenar dörtgen, dört kenarlı ve tüm kenar uzunlukları birbirine eşit bir dörtgendir. Oyun kâğıtlarında görülen eşkenar dörtgene karo, bu şekle sahip olan haplara lozanj, bu şekle sahip olan beyzbol oyun sahasına diamond (elmas) denir.
Yamuk, iki kenarı paralel olan dörtgen. Paralel olan kenarlarına "yamuğun tabanları", paralel olmayan kenarlarına ise "yanal kenarlar" adı verilir.
Öklid geometrisinde deltoid, tabanları çakışık iki ikizkenar üçgenin oluşturduğu dörtgendir.
Benzerlik iki ya da daha fazla cismin, ölçülerinin oranının aynı olmasına denir ve 
sembolüyle gösterilir. Benzerlikte de eşlikte olduğu gibi karşılaştırılan cisimlerin birbirlerine göre konumları ve yönleri oranı bozmaz.
Ruşnik, yüzyıllardan beri geleneksel olarak kullanılan işlemeli geleneksel bir tür kumaş. Bu kumaş türüne Doğu Slavları tarafından kutsallık atfedilmiştir. Dini ritüeller, düğünler ve cenazeler gibi törensel etkinliklerde sıkça kullanılmaktadır. Her bölgenin, nesilden nesile aktarılan ve etnograflar tarafından inceleme konusuna sahip çeşitli şifreli anlamlar içeren kendi tasarımları ve desenleri vardır.
Öklid geometrisinde, Batlamyus teoremi, bir kirişler dörtgeninin dört kenarı ile iki köşegeni arasındaki bir ilişkiyi gösteridir. Teorem, Yunan astronom ve matematikçi Batlamyus'un adını almıştır. Batlamyus, teoremi astronomiye uyguladığı trigonometrik bir tablo olan kirişler tablosunu oluşturmaya yardımcı olarak kullandı.
Leonhard Euler (1707–1783) adını taşıyan Euler dörtgen teoremi veya Euler'in dörtgenler yasası, dışbükey bir dörtgenin kenarları ile köşegenleri arasındaki ilişkiyi açıklar. Pisagor teoreminin genellemesi olarak görülebilecek Paralelkenar yasasının bir genellemesidir. Bu nedenle Pisagor teoreminin dörtgenler açısından yeniden ifade edilmesi bazen Euler-Pisagor teoremi olarak adlandırılır.
Öklid geometrisinde, Batlamyus eşitsizliği, düzlemde veya daha yüksek boyutlu bir uzayda dört nokta tarafından oluşturulan altı uzunluğu ilişkilendirir. Herhangi bir A, B, C ve D noktası için aşağıdaki eşitsizliğin geçerli olduğunu belirtir:
.
Öklid geometrisinde, bir çift merkezli dörtgen, hem bir iç teğet çembere hem de çevrel çembere sahip olan bir dışbükey (konveks) dörtgendir. Bu çemberlerin çevreleri, yarıçapları ve merkezlerine sırasıyla iç çap (inradius) ve çevrel çap (circumradius), iç merkez (incenter) ve çevrel merkez (circumcenter) denir. Tanımdan, çift merkezli dörtgenlerin hem teğetler dörtgeninin hem de kirişler dörtgeninin tüm özelliklerine sahip olduğu anlaşılmaktadır. Bu dörtgenler için diğer isimler kiriş-teğet dörtgeni ve iç teğet ve dış teğet dörtgenidir. Ayrıca nadiren çift çemberli dörtgen ve çift işaretlenmiş dörtgen olarak adlandırılmıştır.
Giordano Vitale veya Vitale Giordano İtalyan matematikçidir. En çok Saccheri dörtgenleri üzerindeki teoremi ile tanınır. Ayrıca Vitale Giordani, Vitale Giordano da Bitonto ve kısaca Giordano olarak da anılır.
Mars'ın yüzeyi, Amerika Birleşik Devletleri Jeoloji Araştırmaları Kurumu tarafından otuz kartografik dörtgene bölünmüştür. Her bir dörtgen, Mars'ın yüzeyinde belirli bir enlem ve boylam aralığını kapsayan bir bölgedir. Bu dörtgenler klasik albedo özelliklerine göre adlandırılmış ve "MC" öneki ile birlikte kuzeyden güneye ve batıdan doğuya doğru birden otuza kadar numaralandırılmışlardır.
Öklid geometrisinde, bir kirişler dörtgeni veya çembersel dörtgen veya çevrimsel dörtgen, köşeleri tek bir çember üzerinde bulunan bir dörtgendir. Bu çembere çevrel çember denir ve köşelerin aynı çember içinde olduğu söylenir. Çemberin merkezi ve yarıçapı sırasıyla çevrel merkez ve çevrel yarıçap olarak adlandırılır. Bu dörtgenler için kullanılan diğer isimler eş çember dörtgeni ve kordal dörtgendir, ikincisi, dörtgenin kenarları çemberin kirişleri olduğu içindir. Genellikle dörtgenin dışbükey (konveks) olduğu varsayılır, ancak çapraz çevrimsel dörtgenler de vardır. Aşağıda verilen formüller ve özellikler dışbükey durumda geçerlidir.
