Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.

Doğru, matematikte mantıksal bir değerdir. Matematik'te ne olduğu belli olmayan (tanımsız) değerlerden biridir. Ayrıca geometride doğru ifadesi aynı doğrultuda olan ve her iki yönden de sonsuza kadar giden noktalar kümesi diye de tanımlanır. Bir doğru üzerinde en az 2 nokta, dışında da en az 1 nokta mevcuttur.

Soyut cebir veya soyut matematik, matematiğin bir alanı olup, cebirsel yapılar üzerinde çalışır. Cebirsel yapılar, elemanları üzerinde belirli işlemlerin uygulandığı kümelerdir ve gruplar, halkalar, alanlar, modüller, vektör uzayları, kafesler ve alan üzerindeki cebirler içerir. Soyut cebir terimi, 20. yüzyılın başlarında temel cebirden ayırmak amacıyla türetilmiştir. Soyut cebir ileri matematik için temel hale geldikçe basitçe "cebir" olarak adlandırılırken, "soyut cebir" terimi pedagoji dışında nadiren kullanılır.

Analitik geometri, geometrik çalışmaya cebrik analizi uygulayan ve cebrik problemlerin çözümünde geometrik kavramları kullanan bir matematik dalı. Bütün bunlar kartezyen sistem denilen bir koordinat sisteminin kullanılmasıyla mümkündür. Kartezyen kelimesi, batıda analitik geometride ilk bilimsel çalışmayı yapan René Descartes'tan gelmektedir.

Günlük kullanımıyla küre kusursuz simetriye sahip geometrik bir nesnedir, bir yüzeydir; üç boyutlu Öklit uzayında (R3) yatar.

Çember ya da dönge, düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktaların kümesinin oluşturduğu yuvarlak, geometrik şekil. Çemberin çevrelediği 2 boyutlu alana daire denir.

Konik kesit, eliptik veya dairesel bir çift taraflı koninin, düzlemle kesitinden meydana gelen eğriler. Bunlar, çember, elips, parabol ve hiperboldür.
Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir nesnedir. a ve b sayıları gerçek olursa karmaşık sayılar şu biçimde gösterilirler:

Vektör uzayı veya Yöney uzayı, matematikte ölçeklenebilir ve eklenebilir bir nesnelerin (vektörlerin) uzayına verilen isimdir. Daha resmî bir tanımla, bir vektör uzayı, iki elemanı arasında vektör toplamasının ve skaler denilen sayılarla çarpımın tanımlı olduğu ve bunların bazı aksiyomları sağladığı kümedir. Skalerler, rasyonal veya reel sayılar kümesinden gelebilir, ama herhangi bir cisim üzerinden bir vektör uzayı oluşturmak mümkündür. Vektör uzayları, skalerlerin geldiği cisime göre reel vektör uzayı, kompleks vektör uzayı veya genel bir cisim üzerinden K vektör uzayı şeklinde adlandırılır.

Karmaşık analiz ya da başka bir deyişle kompleks analiz, bir karmaşık değişkenli fonksiyonları araştıran bir matematik dalıdır. Bir değişkenli karmaşık analize ya da çok değişkenli karmaşık analizle beraber tümüne karmaşık değişkenli fonksiyonlar teorisi de denilir.

Matematikte karmaşık düzlem, gerçel eksen ve ona dik olan sanal eksen tarafından oluşturulmuş, karmaşık sayıların geometrik bir gösterimidir. Karmaşık sayının gerçel kısmının x-ekseni boyuncaki yer değiştirmeyle, sanal kısmının ise y-eksenindeki yer değiştirmeyle temsil edildiği değiştirilmiş bir Kartezyen düzlem olarak düşünülebilir.

Cebirsel topoloji, topolojik uzayları cebirsel gereç ve yöntemlerle inceleyen matematik dalı. Matematikte bir kümenin üzerine döşenecek yapı, yönelinen matematik dalını belirler. Bir kümeye bir ya da birkaç işlem konarak sayılar kuramı ya da cebir yapmaya başlanabilir. Kümenin üzerine bir topoloji koyaraksa topoloji ve, ayrıca uzunluk koyarsak, geometri yapmaya başlanır. Üzerine topoloji konmuş bir uzayı incelemek için kimi cebirsel, aritmetik veya topolojik değişmezler tanımlanır; bunlar aracılığıyla topolojik uzayın özellikleri ayırdedilir. Örneğin tıkızlık, bağlantılılık, sayılabilirlik bu tür değişmezlerdir. Topolojik eşyapısal iki uzaydan biri bu değişmeze sahipse diğeri de buna sahip olmalıdır. Yani, eğer iki uzay için ayrı ayrı bakılan bir değişmez aynı değilse, bu iki uzay eşyapısal olmayacaktır. Yukarıda anılan en eski değişmezlerin hemen ardından inşa edilen klasik değişmezler cebirsel olanlardır.

Matematikte gerçel, karmaşık veya daha genel bir anlamda vektör değerli bir fonksiyonun kökü, fonksiyonun tanım kümesinde bulunan ve fonksiyonun 0 değerini aldığı noktalardır. Yani, eğer bir V kümesinden bir W vektör uzayına tanımlı bir fonksiyonu


Bézout teoremi, cebirsel geometride n değişkenli n polinomun ortak sıfırlarının sayısı ile ilgili bir ifadedir. Orijinal biçiminde teorem, genel olarak ortak sıfırların sayısının, polinomların derecelerinin çarpımına eşit olduğunu belirtir. Adını Fransız matematikçi Étienne Bézout'dan almıştır.

Simetri yalnızca geometride değil, matematiğin diğer dallarında da ortaya çıkar. Simetri bir tür değişmezliktir: matematiksel bir nesnenin bir dizi işlem veya dönüşüm altında değişmeden kaldığı özelliktir.
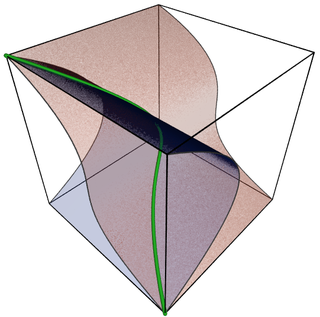
Cebirsel varyeteler, matematiğin bir alt alanı olan cebirsel geometride çalışmanın ana nesneleridir. Klasik olarak cebirsel çeşitlilik, bir polinom denklem sisteminin gerçek veya karmaşık sayılar üzerindeki çözüm kümesi olarak tanımlanır. Modern tanımlamalar orijinal tanımın arkasındaki geometrik sezgiyi korumaya çalışırken kavramı birkaç farklı şekilde genelleştirir.

Matematikte, bir parametrik denklem, bir grup niceliği parametreler olarak adlandırılan bir veya daha fazla bağımsız değişkenin fonksiyonları olarak tanımlar. Parametrik denklemler genellikle bir eğri veya yüzey gibi geometrik bir nesneyi oluşturan noktaların koordinatlarını ifade etmek için kullanılır ve sırasıyla parametrik eğri ve parametrik yüzey olarak adlandırılır. Bu gibi durumlarda, denklemler, toplu olarak nesnenin parametrik temsili veya parametrik sistem, veya parametrelendirilmesi olarak adlandırılır.
Matematikte, bir düzlem eğrisi veya düzlemsel eğri, bir düzlem içinde yer alan bir eğri olup söz konusu düzlem, bir Öklid düzlemi, bir afin düzlem veya bir projektif düzlem olabilir. En sık çalışılan durumlar, düzgün düzlem eğrileri ve cebirsel düzlem eğrisidir.

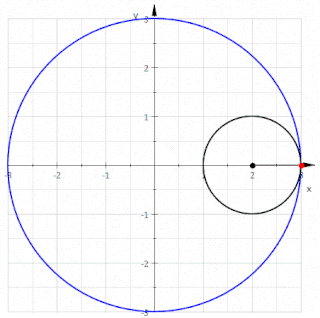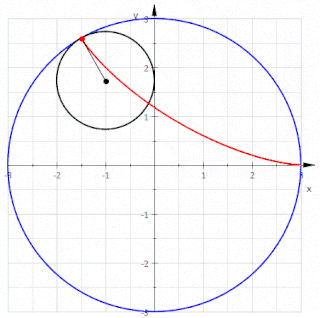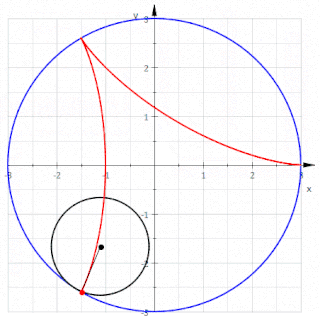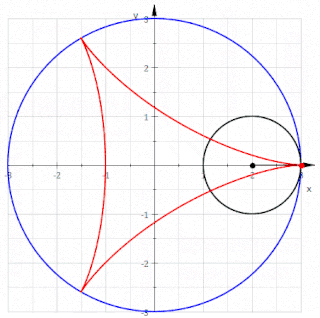
Geometride, triküspoid eğri veya Steiner eğrisi olarak da bilinen deltoid eğri, üç çentikten oluşan bir hiposikloiddir. Başka bir deyişle, bir çemberin çevresi üzerindeki bir noktanın, yarıçapının üç veya bir buçuk katı olan bir çemberin içinde kaymadan yuvarlanırken oluşturduğu yuvarlanma eğrisidir. Adını, benzediği büyük Yunanca delta (Δ) harfinden alır.




















