CBC-MAC

Kriptografide, CBC-MAC, bir blok şifreleme ile mesaj kimlik doğrulama kodu oluşturmak için kullanılır. Mesaj, her blok önceki bloğun düzgün şifrelenmesine bağlı olacak şekilde, bir blok zinciri oluşturmak için CBC kipinde bir blok şifreleme algoritmasıyla şifrelenir. Bu bağlılık sayesinde, şifresiz metnin herhangi bir bitinde yapılan değişikliğin, şifrelenmiş son bloğun, blok şifreleme anahtarı bilinmeden tahmin edilmesini veya etkisiz hale getirilmesini engeller.

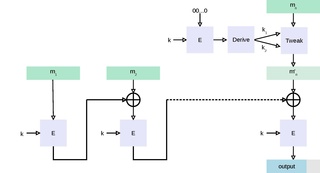
m mesajı için CBC-MAC hesaplarken m CBC kipinde ilklendirme vektörü ile şifrelenir ve son blok tutulur. Aşağıdaki şekil, ${\displaystyle m_{1}\|m_{2}\|\cdots \|m_{x}}$ bloklarından oluşan bir mesaj için, gizli anahtar k ve bir blok şifre E kullanarak CBC-MAC hesaplamasını göstermektedir.

Eğer kullanılan blok şifreleme güvenliyse (pseudorandom bir permütasyon ise),CBC-MAC sabit uzunluktaki mesajlar için güvenlidir.^[1] Ancak, tek başına, değişken uzunluklu mesajlar için güvenli değildir. . Nitekim, herhangi tek anahtar sadece sabit ve bilinen uzunluktaki mesajlar için kullanılmalıdır. . Bunun sebebi ise, İki mesaj için doğru mesaj-etiket çiftlerini bilen saldırgan, ${\displaystyle (m,t)}$ ve ${\displaystyle (m',t')}$, CBC-MAC'i ${\displaystyle t'}$ olan üçüncü bir mesaj ${\displaystyle m''}$ üretebilir. Bu, ${\displaystyle m'}$ ilk bloğunu t ile xorladıktan sonra m mesajını değiştirilmiş ${\displaystyle m'}$ ile birleştirilerek yapılır; diğer bir deyişle ${\displaystyle m''=m\|[(m_{1}'\oplus t)\|m_{2}'\|\dots \|m_{x}']}$ ile yapılır. ${\displaystyle m''}$ mesajı için MAC hesaplanırken, öncelikle m için Mac'i t deki gibi klasik şekilde hesaplanır, ama bu değer ilerideki${\displaystyle E_{K_{\text{MAC}}}(m_{1}'\oplus t)}$ hesaplayan bir adıma zincirlendiğinde, ilk mesajdaki macten ürettilen değer ile birlikte özel or operasyonu gerçekleştirilir. Yeni mesajda etiketin var olması, ilk m mesajındaki şifresiz metin bloklarından üretilen mac'e etki bırakmadan iptal edileceği anlamına gelir:${\displaystyle E_{K_{\text{MAC}}}(m_{1}'\oplus t\oplus t)=E_{K_{\text{MAC}}}(m_{1}')}$böylece ${\displaystyle m''}$ için etiket ${\displaystyle t'}$ dir.

Bu problem, sona mesaj boyutunda blok eklemek ile çözülemez.^[2] CBC-MAC in değişken uzunluklu mesajlar için güvenli yapabilecek şekilde değiştirildiği üç ana yöntem vardır; 1) Girdi boyutlu anahtar ayırmak; 2) başa uzunluk eklemek; 3) son bloğu şifrelemek. Öyle bir durumda, farklı bir blok şifre çalışma kipi kullanılması önerilebilir, örneğin, değişken boyutlu mesajın bütünlüğünü korumak için CMAC veya HMAC.

Bir çözüm yöntemi olarak, mesaj uzunluğunu ilk blokta bulundurmaktır;^[3] herhangi iki birbirinin prefixi olan mesaj kullanılmadığı sürece CBC-MAC'in güvenli olduğu kanıtlanmıştır ve uzunluğu başa eklemek bunun özel bir durumudur.^[4] İşlem başladığında mesajın uzunluğu bilinmiyorsa problemler oluşabilir.

CBC-MACte son bloğu şifrelemek (ECBC-MAC),^[5] CBC-MAC-ELB(m, (k₁, k₂)) = E(k₂, CBC-MAC(k₁, m))^[2] şeklinde tanımlanır. Bahsedilen diğer yöntemlerden olan CBC-MAC'i değişken uzunluklu mesajlar için uzatmaya göre, son bloğu şifrelemenin avantajı hesaplama bitene kadar mesaj uzunluğunun bilinmesinin gerekmemesidir.

Birçok kriptografik şemada olduğu gibi, şifrelerin ve protokollerin naif kullanımı, kriptografik korumanın etkenliğini düşürüp (hatta işe yaramaz hale getirip) saldırıları mümkün kılabilir. CBC-MAC'in yanlış kullanımından kaynaklanan saldırılardan bahsedeceğiz.^[6]

Aynı anahtar k'yi CBC şifreleme ve CBC-MAC için yeniden kullanmak yaygın bir hatadır. Her ne kadar bir anahtarın farklı amaçlar için yeniden kullanılması genel olarak kötü bir uygulama olsa da, bu özel durumda bir saldırıya sebep olur:

Diyelim ki Alice Bob'a şifre metin blokları ${\displaystyle C=C_{1}\|C_{2}\|\dots \|C_{n}}$ göndermiş olsun. Aktarma işlemi sırasında Eve, son metin bloğu ${\displaystyle C_{n}}$ aynı kalacak şekilde, şifre metni bloklarından herhangi birini karıştırabilir ve seçtiği bitleri istediği gibi ayarlayabilir. Bu örneğin amaçları doğrultusunda başlangıç vektörünün sıfırlar vektörü olduğunu varsayıyoruz.

Bob mesajı aldığında, şifre metin bloklarını ${\displaystyle C=C_{1}\|C_{2}\|\cdots \|C_{n}}$ kullanarak, Alice'in uyguladığı şifleme işlemi tersine çevirerek mesajın şifresini çözecektir. Bob'a gelen, Alice'in orijinal mesajı yerine karıştırılmış olan mesaj ${\displaystyle C'=C_{1}'\|\dots \|C_{n-1}'\|C_{n}}$ .

Bob önce, şifresiz metni elde etmek için paylaşılan gizli anahtar K kullanarak mesajın şifresini çözer. Eve sonuncu hariç bütün şifreli metin bloklarını değiştirdiği için, üretilen bütün şifresiz metin Alice'in gönderdiğinden farklı olacak. Özellikle, son şifresiz metin, ${\displaystyle P_{n}'}$, Alice'in gönderdiği orijinal ${\displaystyle P_{n}}$'den farklıdır; ${\displaystyle C_{n}}$ aynı olsa da, ${\displaystyle C_{n-1}'\not =C_{n-1}}$ bu nedenle şifre çözme işleminden sonra önceki şifre bloğunu özel OR'a zincirlerken farklı ${\displaystyle P_{n}'}$ üretilir.${\displaystyle P_{n}'=C_{n-1}'\oplus E_{K}^{-1}(C_{n})}$

Bob, çözdüğü tüm düz metin değerleri üzerinden CBC-MAC kullanarak kimlik doğrulama etiketini hesaplar. Yeni mesajın etiketi olan ${\displaystyle t'}$, şu şekilde elde edilir:

${\displaystyle t'=E_{K}(P_{n}'\oplus E_{K}(P_{n-1}'\oplus E_{K}(\dots \oplus E_{K}(P_{1}'))))}$

Bu ifadeler eşittir,

${\displaystyle t'=E_{K}(P_{n}'\oplus C_{n-1}')}$

tam olarak hangisi ${\displaystyle C_{n}}$ :

${\displaystyle t'=E_{K}(C_{n-1}'\oplus E_{K}^{-1}(C_{n})\oplus C_{n-1}')=E_{K}(E_{K}^{-1}(C_{n}))=C_{n}}$

buradan ${\displaystyle t'=C_{n}=t}$ çıkarılır.

Bu nedenle Eve, iletilmekte olan şifre metnini (hangi şifresiz metne karşılık geldiğini bilmeden) değiştirebildi, öyle ki tamamen farklı bir mesaj, ${\displaystyle P'}$, üretildi ama bu mesajın etiketi orijinal mesajın etiketiyle eşleşti ve Bob iletim aşamasında mesajın içeriğinin değiştirildiğinden habersizdi. Tanım olarak, önceki mesajla (P) aynı etiketi üreten farklı bir mesaj (şifresiz metin dizisi ${\displaystyle P'}$ ve ${\displaystyle P\not =P'}$) bulabilirsek mesaj kimlik doğrulama kodu bozuktur deriz. Bu senaryoda, mesaj kimlik doğrulama protokolünün bozulduğu ve Bob'un Alice'in üretmediği bir mesaj gönderdiğine inanmak için aldatılmıştır.

Bunun yerine, şifreleme ve kimlik doğrulama aşamaları için farklı anahtarlar kullanırsak, ${\displaystyle K_{1}}$ ve ${\displaystyle K_{2}}$, saldırı başarısız olurdu. Değiştirilmiş şifreli metin bloklarının,${\displaystyle C_{i}'}$, şifresinin çözülmesi şifresiz metin dizisi, ${\displaystyle P_{i}'}$, sağlar. Ancak, MACin farklı bir${\displaystyle K_{2}}$ anahtarını kullanması nedeniyle, aynı etiketi üretmek için ileti kimlik doğrulama kodunun hesaplanmasının ileri adımında şifre çözme işlemini "geri çeviremeyiz"; değiştirilmiş her ${\displaystyle P_{i}'}$  artık CBC-MAC işleminde ${\displaystyle K_{2}}$ ile ${\displaystyle \mathrm {MAC} _{i}\not =C_{i}'}$ değerine şifrelenecek.

Bu örnek aynı zamanda CBC-MAC'in çarpışmaya dayanıklı tek yönlü bir fonksiyon olarak kullanılamayacağını da göstermektedir: bir anahtar verildiğinde, aynı etikete "özet"(hash?) yapan farklı bir mesaj oluşturmak önemsizdir.

Şifreleme bloğu zincirleme (veya bir başka) kip içinde bir blok şifreleyici kullanarak verileri şifrelerken, şifreleme işleminin ilk aşamasına bir başlatma vektörü eklemek yaygındır.

Tipik olarak bu vektörün rastgele seçilmesi (tek seferlik anahtar) ve blok şifresinin çalıştığı herhangi bir gizli anahtar için tekrar edilmemesi gerekir. Bu, aynı düz metnin aynı şifre metnine şifrelenmemesini sağlayarak, saldırganın bir ilişki oluşturmasına izin verir semantik güvenlik sağlar.

Bir başlatma vektörünün CBC-MAC gibi bir mesaj kimlik doğrulama kodu hesaplanırken kullanılması olası bir saldırı vektörüdür.

Bir şifre bloğu zincirleme şifresinin çalışmasında, düz metnin ilk bloğu başlatma vektörü ile özel OR kullanılarak karıştırılır (${\displaystyle P_{1}\oplus IV}$). Bu işlemin sonucu, şifreleme işlemi için blok şifrelemenin girdisidir.

Ancak, şifreleme ve şifre çözme işlemleri gerçekleştirilirken, ilklendirme vektörü şifresiz metinle göndermekle yükümlüyüz -tipik olarak şifreli metnin ilk bloğundan önceki blok olarak- bu şekilde şifresiz metnin ilk bloğunun şifresi çözülebilir ve başarıyla kurtarılabilir. Eğer bir MAC hesaplıyorsanız, mesajdaki etiketin hesaplanan değer ile eşleştiğini doğrulayabilmek için ilklendirme vektörünü diğer tarafa şifresiz metin ile iletmemiz gerekecektir.

Eğer ilklendirme vektörünün keyfi olarak seçilmesine izin verilirse, aynı mesaj etiketi oluşturulurken ilk şifresiz metin bloğu değiştirilebilir (farklı bir mesaj ileterek).

Bir mesaj düşünün ${\displaystyle M_{1}=P_{1}|P_{2}|\dots }$ . Özellikle, CBC-MAC için mesaj etiketini hesaplarken, bir ${\displaystyle IV_{1}}$ ilklendirme vektörü seçtiğimizi varsayalım, öyle ki MAC'ın hesaplanması ${\displaystyle E_{K}(IV_{1}\oplus P_{1})}$ ile başlasın. Bu bir (mesaj, etiket) çifti üretir ${\displaystyle (M_{1},T_{1})}$ .

Şimdi ${\displaystyle M_{2}=P_{1}'|P_{2}|\dots }$ mesajı üret. ${\displaystyle P_{1}'}$ içindeki değiştirilmiş her bit için, ilklendirme vektöründe karşılık gelen bitler çevirilir ve ${\displaystyle IV_{1}'}$ ilklendirme vektörü üretilir. Bu mesaj için MAC'ı hesaplarken şu işlem ile başlıyoruz: ${\displaystyle E_{K}(P_{1}'\oplus IV_{1}')}$. Hem şifresiz metin hem ilklendirme vektörü bitleri aynı yerde değiştirildiği için, ilk aşamada değişiklik iptal edilir, yani blok şifre girişi ${\displaystyle M_{1}}$ için olan ile aynıdır. Eğer şifresiz metinde başka değişiklik yapılmazsa, farklı bir mesaj iletiliyor olsa dahi aynı etiket üretilir.

İlklendirme vektörü seçme özgürlüğü kaldırılırsa ve tüm CBC-MAC implementasyonları belirli bir ilklendirme vektörüne sabitlenirse(genelde sıfır vektörü ancak herhangi bir şey olabilir) bu saldırı devam edemez.

Özetlemek gerekirse, saldırgan MAC doğrulaması için kullanılacak IV'ü belirleyebiliyorsa, MAC'i geçersiz kılmadan ilk veri bloğunda keyfi değişiklik yapabilir.

Bazen IV, mesaj tekrar saldırılarını önlemek için bir sayaç olarak kullanılır. Ancak, saldırgan MAC doğrulaması için hangi IV'ün kullanılacağını tahmin edebiliyorsa, doğrulama için kullanılacak IV'deki değişikliği telafi etmek için ilk veri bloğunu değiştirerek önceden gözlemlenen mesajı tekrar dinleyebilir. Örneğin saldırgan ${\displaystyle IV_{1}}$ ile birlikte ${\displaystyle M_{1}=P_{1}|P_{2}|\dots }$mesajını gözlemlemişse ve ${\displaystyle IV_{2}}$biliyorsa ${\displaystyle M_{1}'=(P_{1}\oplus IV_{1}\oplus IV_{2})|P_{2}|\dots }$ üretebilir, ${\displaystyle IV_{2}}$ ile MAC doğrulamasını geçer.

En basit karşı tedbir, IV kullanmadan önce şifrelemektir (yani IV'ü veriler için hazırlamak). Alternatif olarak CFB kipindeki MAC kullanılabilir, çünkü CFB kipinde IV verilerle XOR edilmeden önce şifrelenir.

Başka bir çözüm olarak (mesaj tekrarı saldırıları koruması gerekli değilse) her zaman sıfır vektörü IV kullanılır.^[7] Yukarıdaki formül ${\displaystyle M_{1}'}$ için ${\displaystyle M_{1}'=(P_{1}\oplus 0\oplus 0)|P_{2}|\dots =P_{1}|P_{2}|\dots =M_{1}}$ haline gelir. ${\displaystyle M_{1}}$ ve ${\displaystyle M_{1}'}$ aynı mesaj olduğu için, tanım gereği aynı etikete sahip olurlar. Bu bir sahtecilik değildir, CBC-MAC'in amaçlanan kullanımıdır.

FIPS PUB 113 Bilgisayar Verileri Kimlik Doğrulaması, CBC-MAC algoritmasını blok şifre olarak DES kullanarak belirleyen bir ABD hükûmet standardıdır (artık kullanılmamaktadır) .

CBC-MAC algoritması ISO / IEC 9797-1 MAC 1 Algoritması'na eşdeğerdir.

• CMAC - Farklı uzunluklardaki mesajlar için güvenli olan (NIST tarafından önerilen) blok şifreleme tabanlı bir MAC algoritması.
• OMAC ve PMAC - Blok şifrelemeleri mesaj kimlik doğrulama kodlarına (MAC) dönüştürmenin diğer yöntemleri.
• Tek yönlü sıkıştırma işlevi - Karma işlevler blok şifrelerden yapılabilir. Ancak, MAC'lar (CBC-MAC gibi) ve karmalar arasında güvenlik için işlev ve kullanımlarda önemli farklılıklar olduğunu unutmayın.