Burun konisi tasarımı
Sıkışabilir akışkan bir ortamda yol alan herhangi bir araç ya da gövde (roket ya da uçak, füze ya da mermi gibi)ye ait burun konisi kısmının aerodinamik tasarımındaki, önemli bir problem burun konisinin geometrik şeklinin belirlenmesidir . Burun konisinin şekli optimum performans için gereklidir. Dönel katı cisim şekil tanımlamasının gerektiği işler gibi birçok uygulamalar, akışkan bir ortamda çok hızlı hareket eden böyle bir cismin karşılaşacağı direncin en aza indirilmesini gerektirir.
Burun konisi şekilleri ve denklemler
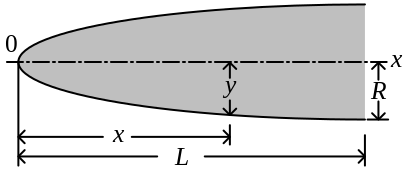
Genel boyutlar
Aşağıdaki burun konisi şekli denklemlerinin tümünde, L burun konisinin toplam uzunluğu ve R burun konisi tabanının yarıçapıdır. y, burun konisinin ucundan L ye kadar değişiklik gösteren herhangi bir x noktasının yarıçapıdır. Denklemler burun konisi şeklinin iki boyutlu profilini tanımlar. Profilin eksen (C/L) etrafında döndürülmesiyle burun konisinin tam bir dönel katı cismi oluşur. Denklemlerin 'mükemmel' bir burun şeklini tanımladığı unutulmamalıdır. Burun konilerinin ucu gerçekte, imalat ya da aerodinamik nedenlerden dolayı çoğu kez küt ya da kesilmiş olmaktadır.
Konik
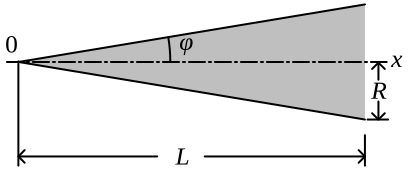
Çok yaygın bir burun konisi şekli basit bir konidir. Bu şekil genellikle üretim kolaylığı için ve aynı zamanda sürükleme özellikleri için de seçilir. Konik bir profilin yan tarafları düz çizgi olduğundan, çap denklemi oldukça basittir:
Koniler bazen yarım açılarıyla da tanımlanabilir, :
- ve
Küresel Kesilmiş Koni

Pratik uygulamalarda, konik bir burun genellikle kürenin bir parçası tarafından kesilmiştir. Koni ile kürenin teğet noktası şu şekilde bulunabilir:
- burada:
- küresel burun yarıçapıdır.
Küresel burnun merkezi:
Ve, tepe noktası ise:
- olur.
Bikonik
Bikonik bir burun konisi şekli, uzunluğu L2 olan kesik bir koni (genellikle konik geçiş parçası olarak bilinir)nin üstünde yer almış uzunluğu L1 olan basit bir konidir. Üstte yer alan R1 yarıçaplı koninin tabanı altta yer almış taban yarıçapı R2 olan kesik koninin üst yarıçapına eşittir.

- L = L1 + L2
- : için
yarım açı :
- ve
- : için
yarım açı :
- ve
Tanjant ojiv
Basit bir koniden sonra model roketçilikte en yaygın burun konisi şekli, tanjant ojiv şeklidir. Bu şeklin profili bir daire kesmesinden oluşur. Roket gövdesi burun konisinin bükeyine teğet geçer. Bu şeklin büyük ölçüde rağbet görmesi profil şeklinin yapım kolaylığından dolayıdır.
Ojivi oluşturan dairenin yarıçapına ojiv yarıçapı denir ve bu yarıçap, burun konisinin taban yarıçapı ve uzunluğuna bağlı olarak formülle ifade edilir:
x in 0 ile L arasındaki değişikliğine göre, herhangi bir x noktasındaki y yarıçapı:
Burun konisi uzunluğu, L, ojiv yarıçapı ^ ‘na eşit ya da ondan daha az olmalıdır . Eşit olmaları halinde şekil bir yarımküre olur.
Küresel kesilmiş tanjant ojiv

Tanjant bir ojiv burun genellikle kürenin bir parçası tarafından kesilmiştir. Tanjant ojiv ile kürenin teğet noktası şu şekilde bulunabilir:
- burada:
- yarıçap ve küresel burnun merkezidir.
Ve, tepe noktası ise:
- olur.
Sekant ojiv
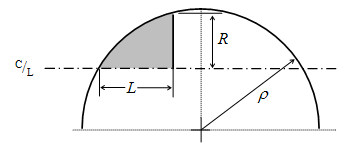
Bu şeklin profili aynı zamanda bir daire kesmesinden oluşsa da şeklin tabanı, ojiv yarıçapı ile tanımlanan dairenin yarıçapı üzerinde değildir. Roket gövdesi burun konisinin bükeyine teğet geçmez. Ojiv yarıçapı R ve L (tanjant ojiv de olduğu gibi) ile belirlenmesinden çok burun şeklini tanımlamak için seçilecek bir faktördür. Seçilen sekant ojivin yarıçapı, R ve L ile aynı olan tanjant ojivin yarıçapından büyükse, sonuçta oluşan sekant ojiv, tabanı kesilmiş bir tanjant ojiv gibi görünecektir.
- ve
x in 0 ile L arasındaki değişikliğine göre, herhangi bir x noktasındaki y yarıçapı:
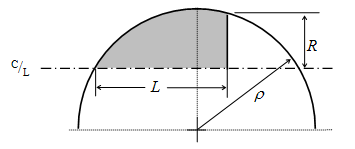
Seçilen tanjant ojiv den küçükse, bu durumda ortaya çıkan sekant ojiv, taban çapından daha büyük bir çıkıntıya sahip olacaktır. Bu şeklin klasik örneği MGR-1 Honest John füzesinin burun konisidir. Ayrıca, seçilen ojiv yarıçapı burun konisi uzunluğunun iki katından daha büyük olmalıdır.
Eliptik
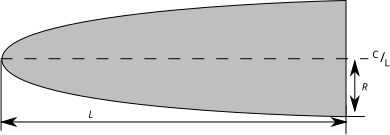
Bu şeklin profili, ekseni ana eksen ve burun konisinin tabanı küçük eksen olan bir elipsin yarısıdır. Ana ekseninin etrafında tam bir dönüş yapan elipse elipsoit adı verildiği için eliptik bir burun şekline yarıelipsoit adı verilir. Bu şekil küt burun ve tanjant tabandan dolayı sesaltı uçuş (model roketçilik gibi)larda çok kulanılır. Bu şekil profesyonel roketçilikte pek kullanılmaz. R L ye eşit olursa, bu bir yarımküre olur.
Parabolik
Genellikle ‘parabolik’ bir burun konisi ifade edilmek istendiğinde, küt bir şekli olmayan bu burun şekli öngörülmektedir. Parabolik serisi burun şekli Latus rectum daki paralel bir çizgi etrafında bir parabol parçasının döndürülmesiyle oluşturulur. Bu yapı bir daireden çok bir parabolü belirleyen şekil olmasının dışında tanjant ojiv şekline benzer. Ojivde olduğu gibi, bu yapı sivri uçlu bir burun şeklini ortaya çıkarır. Genellikle, parabolik bir burun ile ilişkililendirilen küt şekil için, kuvvet serisi kısmına bakınız(Parabolik şekil çoğu kez eliptik şekille karıştırılır).
: için
K' 0 ile 1 arasında herhangi bir yerde değişebilse de, burun koni şekilleri için en çok kullanılan değerler şunlardır:
- Bir koni için; K’ = 0
- ½ bir parabol için; K’ = 0.5
- 3/4 bir parabol için; K’ = 0.75
- Tam bir parabol için; K’ = 1
Tam Parabol (K'=1) olması durumunda, burun şekli parabol ekseni üzerinde bulunan tabandaki gövdeye teğettir. K' değerleri 1'den daha az olduğunda, görünümü sekant ojive benzeyen ‘daha ince’ bir şekil ortaya çıkar. Şekil artık tabana teğet olmayıp, parabol ekseni kaymış olmasına rağmen taban paralel kalır.
Kuvvet serisi
Kuvvet Serileri genellikle ‘parabolik’ bir burun konisi olarak anılan şekli içerse de, parabolik bir burun konisi olarak bilinen şekil parabolik seri'nin bir öğesi olup tamamen farklı bir şeydir. Kuvvet serisi şekli (genellikle) küt ucuyla karakterize edilirse de gerçekte tabanı gövde borusuna teğet değildir. Burun konisi / gövde ek yerinde hava aracının aerodinamiğine zarar verebilen daima bir kesiklik vardır. Bu kesikliliği düzeltmek için şekil, alt kısmında değişikliğe uğratılabilir. Hem silindir ve hem de bir koni kuvvet serisinin üyeleridir.
1'den daha az n değerleri için, kuvvet serisi burun şekli y = R(x/L)^n eğrisinin x-ekseni etrafında döndürülmesiyle oluşturulur. n faktörü şeklin ‘kütlüğünü’ kontrol eder. 0.7 ve üzerindeki n değerleri için, burun ucu oldukça incedir. n değeri sıfıra doğru yaklaştıkça, Kuvvet Serisi burun şekli gittikçe kütleşir.
için
Burada:
- Bir koni için; n = 1
- 3/4 bir kuvvet için; n = 0.75
- ½ bir kuvvet (parabol) için; n = 0.5
- Bir silindir için; n = 0
Haack serisi
Yukarıdaki bütün burun şekillerinden farklı olarak, Haack Serisi şekilleri geometrik şekillerden yapılmamıştır. Şekiller, matematiksel olarak değil de sürüklemeyi en aza indirmek amacıyla elde edilmiştir. Haack serisi aşağıdaki denklemde C değeri vasıtasıyla belirlenirken, C nin iki değeri özel bir öneme sahiptir: C = 0 olduğunda, LD simgesi verilen boy ve çap için, minimum sürüklenmeyi belirtir . C = 1/3 olduğunda ise, LV verilen boy ve hacim için minimum sürüklenmeyi belirler. C = 2/3 hariç olmak üzere, Haack serisi burun konileri gövdeye tabanlarından tamamen teğet değildir. Ancak, kesiklik genellikle fark edilmeyecek kadar önemsizdir. C > 2/3 için, Haack burun konileri taban çapından daha büyük maksimum bir çaplı çıkıntı yapar. Haack burun uçları sivri olmasalar da biraz yuvarlaktırlar.
Burada:
- LV-Haack için; C = 1/3
- LD-Haack için; C = 0
Von Kármán
Haack serisi verilen boy ve çap için(LD-Haack), minimum sürüklenmeyi verir ve genellikle Von Kármán ya da Von Kármán Ojiv olarak bilinir.
Aerospik
Sürüklemeyi azaltıcı aerospik başlığına bakınız.
Burun konisi sürüklenme özellikleri
Uçak ve roketler için, 0.8 Mach'in altında, burun basınç sürüklemesi esasen tüm şekiller için sıfırdır. En önemli faktör olan yüzey sürtünme sürüklemesi, büyük ölçüde şekildeki yüzeyin düzgünlüğüne ve yüzey kusurlarının varlığına (ıslak alan)a bağlıdır. Örneğin, sesaltı roketler için genellikle kısa, küt, düzgün bir eliptik şekil tercih edilir. Basınç sürüklenmesinin önemli ölçüde arttığı transonik ve ötesi alanlarda, sürükleme üzerine burun şeklinin etkisi çok önemli olmaktadır. Basınç sürüklemesini etkileyen faktörler burun konisinin genel şekli olan, incelik oranı ve düzgünlük oranıdır.
Genel şeklin etkisi
Burun konisi tasarımı ile ilgili birçok referanslar, farklı uçuş rejimlerindeki çeşitli burun şekillerinin sürüklenme özelliklerini karşılaştıran deneysel veriler içerir. Burada sunulan grafik bu verileri en kapsamlı ve kullanışlı olarak göstermektedir. Bu grafik diğer referanslarla daha da ayrıntılı hale getirilebilinirse de diğer referanslarda daha az kapsamlı veriler bulunmaktadır (özellikle USAF Datcom).

Birçok burun konisi tasarımlarında, en büyük sıkıntı 0.8 - 1.2 Mach arasındaki hıza sahip olan transonik bölgedeki uçuş performansıdır. Transonik bölgedeki değişik şekiller için mevcut veri olmamasına rağmen, tablo Von Kármán şeklini ya da n = ½ olan Kuvvet Serisi şeklini açıkça göstermektedir. Bu uçuş için konik ya da ojiv şekiller, daha uygun olacaktır.
Bu gözlem, ses duvarını aşmak için, konik bir burun konisinin uygun olduğunu sıklıkla iddia eden genel kanının aksi bir durumunu yansıtmaktadır. Transonik bölge için en iyi hale getirilen burun şekillerinin örnekleri belki de savaş uçaklarında olmasına rağmen burun şekilleri, hava girişleri ve uçakların elektronik sistemlerinden dolayı çoğu kez bozulmuştur. Örneğin, bir F-16 burnu Von Karman şekline çok benzemektedir.
İncelik oranının etkisi
Bir burun konisinin boyunun taban çapına oranı incelik oranı olarak adlandırılır. Bu terim, kanatlar ve kanatçıklara uygulansa da bazen kanat açıklık oranı adı da verilmektedir. İncelik oranı çoğu kez aracın bütün boyu ve çapı dikkate alınarak tamamına uygulanır. Boy/çap oranına çoğu kez burun konisinin ölçüsü de denir. Süpersonik hızlarda, incelik oranı özellikle düşük oranlarda burun konisi dalga sürüklemesi üzerinde önemli bir etkiye sahip olsa da 5:1 oranının ötesindeki artan oranlar için çok az ek kazanç vardır. İncelik oranının artması ile, ıslak alan ve bu nedenle sürükleme bileşeni olan yüzey sürtünmesi artacaktır. Bu nedenle, azalan dalga sürüklemesi ve artan yüzey sürtünme sürüklemesi arasında oluşan bir değiş tokuşla en sonunda minimum sürükleme incelik oranı ortaya çıkacaktır.
Yararlanılan kaynaklar
- The Descriptive Geometry Of Nose Cones11 Nisan 2011 tarihinde Wayback Machine sitesinde arşivlendi.
- Nose cones equations[]
- Chin SS. (1961). Missile Configuration Design. McGraw-Hill Book Co., Inc., New York.