İçeriğe atla

Bulanık mantık

Bulanık mantık, bulanık eseme ya da puslu mantık, 1965 yılında Lütfü Aliasker Zade'nin yayınladığı bir makalenin sonucu oluşmuş bir mantık yapısıdır.[1]

Bulanık mantığın temeli bulanık küme ve alt kümelere dayanır. Klasik yaklaşımda bir nesne ya kümenin elemanıdır ya da değildir. Matematiksel olarak ifade edildiğinde nesne küme ile olan üyelik ilişkisi bakımından kümenin elemanı ise "1", kümenin elemanı değilse "0" değerini alır. Bulanık mantık klasik küme teorisinin genişletilmesidir. Bulanık kümede her bir nesnenin bir üyelik derecesi vardır. Nesnenin üyelik derecesi, (0, 1) aralığında herhangi bir değer olabilir ve üyelik fonksiyonu M(x) ile gösterilir.

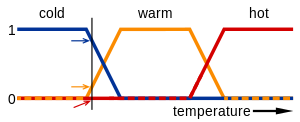
Örneğin; normal oda sıcaklığını 23 derece olarak kabul edersek klasik küme kuramına göre 23 derecenin üzerindeki sıcaklık derecelerini sıcak olarak kabul ederiz ve bu derecelerin sıcak kümesindeki üyelik dereceleri "1" olur. 23 altındaki sıcaklık dereceleri ise soğuktur ve sıcak kümesindeki üyelik dereceleri "0" olur. Soğuk kümesini temel aldığımızda bu değerler tersine döner. Bulanık küme yaklaşımında üyelik değerleri [0,1] aralığında değerler almaktadır. Örneğin 14 derecelik sıcaklık için üyelik derecesi "0", 23 sıcaklık derecesi için üyelik değeri "0,25" olabilir.

Klasik kümelerin aksine bulanık kümelerde elemanların (nesnelerin) üyelik dereceleri [0, 1] aralığında sonsuz sayıda değişebilir. Bunlar üyelik derecelerinin devamlı ve aralıksız bütünüyle bir kümedir. Kesin kümelerdeki soğuk-sıcak, hızlı-yavaş, aydınlık-karanlık gibi ikili değişkenler, bulanık kümelerde biraz soğuk, biraz sıcak, biraz karanlık gibi esnek niteleyicilerle genişletilerek gerçek dünya problemlerine benzetilir. Kesin kümelerden farkı ise böyle bir çatıda bilginin kaynağındaki küme üyeliğinin, kesin tanımlanmış ön koşullarının olmayışı ve değişkenlerin belli bir aralıkta bulunmasıdır.

Bir şeyin varlığı kendisine ait bir isimle doğar. Evrendekilerin tamamı hem (ya) tek (1) hem de (ya da) sonsuz eksi tektir (sonsuz - 1).

Klasik mantık ile bulanık mantık arasındaki temel farklılıklar:

Klasik Mantık Bulanık Mantık
A veya A Değil A ve A Değil
Kesin Kısmi
Hepsi veya Hiçbiri Belirli Derecelerde
0 veya 1 0 ve 1 Arasında Süreklilik
İkili Birimler Bulanık Birimler

Yapay zekâ uygulaması olarak bulanık mantık

Bulanık mantık bir yapay zekâ uygulaması oluşturma prensibidir. Bulanık mantıkta temel olan bir sonuca varmaktır. Normal bir programın yapısı:

  • Temel girdiler → Program → Sabit bir sonuç şeklindedir. Oysaki bir bulanık mantık uygulaması:
  • Sayısı belli olmayan veri yığını → Program → Girdilere ve varsayıma göre değişken bir veya birden fazla sonuç şeklindedir. Bir bulanık mantık uygulamasındaki sonuç, aynı girdiler olsa bile değişik bir sonuç döndürebilir ve bir öbek halinde veriyi alabilir. Bulanık mantıktaki özellik bunun haricinde verilen verilerin örnekleme mantığı ile alınması ve tümü simgelediği varsayımı yapılması ve buna göre bir olasılık değerinin elde edilmesidir.

Yapay zekâda bulanık mantık uygulamaları

Bulanık mantık, kesin çıktıyı elde etmek için girdi olasılıklarının seviyeleri üzerinde çalışır. Küçük mikro denetleyicilerden büyük, ağa bağlı, iş istasyonu tabanlı denetim sistemlerine kadar çeşitli boyut ve yeteneklere sahip sistemlerde uygulanabilir. Bulanık mantık, donanım, yazılım veya her ikisinin bir kombinasyonunda uygulanabilir. Bulanık mantık ticari ve pratik amaçlar için kullanışlıdır; makineleri ve tüketici ürünlerini kontrol edebilir, doğru akıl yürütmeyebilir, ancak kabul edilebilir mantık yürütebilir. Bulanık mantık, ayrıca mühendislikteki belirsizlikle başa çıkmaya yardımcı olur.

Bulanık mantığın kullanıldığı alanlar

Bulanık mantık için temel uygulama alanları aşağıdaki gibidir:

Otomotiv sistemleri

  • Otomatik şanzımanlar
  • Dört tekerli taşıtlar
  • Araç ortam kontrolü

Tüketici elektroniği ürünleri

Beyaz eşyalar ve ev aletleri

İklimlendirme ürünleri

Bulanık mantık sistemlerinin avantajları

  • Bulanık akıl yürütme içindeki matematiksel kavramlar çok basittir.
  • Bulanık mantığın esnekliğinden dolayı, sadece kurallar ekleyerek veya silerek bir FLS'yi (bulanık mantık sistemi) değiştirebilirsiniz.
  • Bulanık Mantık Sistemleri kesin olmayan, bozuk, gürültülü giriş bilgileri alabilir.
  • FLS'lerin oluşturulması ve anlaşılması kolaydır.

Bulanık mantık sistemlerinin dezavantajları

  • Bulanık sistem tasarımına sistematik bir yaklaşım yoktur.
  • Sadece basit olduklarında anlaşılabilirler.
  • Yüksek doğruluk gerektirmeyen problemler için uygundurlar.

Ayrıca bakınız

Kaynakça

  1. ^ Aydın, Şamil Emre (2017). Yapay Zekâ Teknolojisi (Yapay Zekâların Dünü Bugünü Yarını). s. 14-15. 8 Ağustos 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Ağustos 2021. 
  • İBRAHİM, Ahmad M. (2006), Gömülü Sistemlerde Bulanık Mantık, Bileşim Yayınları, 198 s.
  • ÖZLEM, Doğan (2000), Mantık Klasik/Sembolik Mantık, Mantık Felsefesi, İnkılap Kitabevi, İstanbul, 398 s.
  • ŞEN, Zekai (2003), Modern Mantık, Bilge Kültür Sanat, 168 s.
  • ŞEN, Zekai (2004), Mühendislikte Bulanık Mantık ile Modelleme Prensipleri, Su Vakfı, 190 s.

Dış bağlantılar

Wikimedia Commons'ta Fuzzy logic ile ilgili çoklu ortam belgeleri bulunur

İlgili Araştırma Makaleleri

Sayı, sayma, ölçme ve etiketleme için kullanılan bir matematiksel nesnedir. En temel örnek, doğal sayılardır. Sayılar, sayı adı (numeral) ile dilde temsil edilebilir. Daha evrensel olarak, tekil sayılar rakam adı verilen sembollerle temsil edilebilir; örneğin, "5" beş sayısını temsil eden bir rakamdır. Yalnızca nispeten az sayıda sembolün ezberlenebilmesi nedeniyle, temel rakamlar genellikle bir rakam sisteminde organize edilir, bu da herhangi bir sayıyı temsil etmenin organize bir yoludur. En yaygın rakam sistemi Hint-Arap rakam sistemidir, bu sistem on temel sayısal sembol, yani rakam kullanılarak herhangi bir negatif olmayan tam sayının temsil edilmesine olanak tanır. Sayılar sayma ve ölçme dışında, etiketlerde, sıralamada ve kodlarda kullanılmak için de sıklıkla kullanılır. Yaygın kullanımda, bir rakam ile temsil ettiği sayı net bir şekilde ayrılmaz.

Matematik felsefesinde, sezgicilik ya da yeni sezgicilik akımı, matematiğe insanların oluşturucu etkinliği olarak bakan bir yaklaşımdır.

Matematiksel mantık, biçimsel mantığın matematiğe uygulanmasıyla ilgilenen bir matematik dalıdır. Metamatematik, matematiğin temelleri ve kuramsal bilgisayar bilimi alanlarıyla yakınlık gösterir. Matematiksel mantığın temel konuları biçimsel sistemlerin ifade gücünün ve biçimsel ispat sistemlerinin tümdengelim gücünün belirlenmesidir.

<span class="mw-page-title-main">Mantık</span> bilginin yapısını inceleyen, doğru ile yanlış arasındaki akıl yürütmenin ayrımını yapan disiplin

Mantık ya da eseme, bilginin yapısını inceleyen, doğru ile yanlış arasındaki akıl yürütmenin ayrımını yapan disiplindir, doğru düşüncenin aletidir. Önceleri bir felsefe dalıyken daha sonra kendi başına bir ihtisas alanı olmuştur. Matematik ve bilgisayar biliminin de parçası haline gelmiştir. Bir disiplin olarak Aristoteles tarafından kurulmuştur. Aristoteles'den etkilenen Farabi tarafından iki kısımda kategorize edilmiştir. İbn-i Sina geçicilik ve içerme arasındaki ilişkiyi geliştirmiştir. Çağdaş zamanlarda Frege, Russell ve Wittgenstein önemli katkılar yapmıştır.

<span class="mw-page-title-main">Radyoaktivite</span> Atom çekirdeğinin kendiliğinden parçalanması

Radyoaktivite, radyoaktiflik, ışınetkinlik veya nükleer bozunma; atom çekirdeğinin, daha küçük çekirdekler veya elektromanyetik ışımalar yayarak kendiliğinden parçalanmasıdır. Çekirdek tepkimesi sırasında veya çekirdeğin bozunması ile ortaya çıkar. En yaygın ışımalar alfa(α), beta(β) ve gamma(γ) ışımalarıdır. Bir maddenin radyoaktivitesi bekerel veya curie ile ölçülür.

<span class="mw-page-title-main">Termodinamik</span> enerji bilimi

Termodinamik; ısı, iş, sıcaklık ve enerji arasındaki ilişki ile ilgilenen bilim dalıdır. Basit bir ifadeyle termodinamik, enerjinin bir yerden başka bir yere ve bir biçimden başka bir biçime transferi ile ilgilenir. Bu süreçteki anahtar kavram, ısının, belirli bir mekanik işe denk gelen bir enerji biçimi olmasıdır.

<span class="mw-page-title-main">Makine</span> herhangi bir enerji türünü başka bir enerjiye dönüştürmek, belli bir güçten yararlanarak bir işi yapmak veya etki oluşturmak için dişliler, yataklar ve miller gibi çeşitli makine elemanlarından oluşan düzenekler bütünü

Makine, bir iş yapmak için kuvvet uygulamak ve hareketi kontrol etmek için güç kullanan fiziksel bir sistemdir. Terim genellikle motor kullanan yapay cihazlara veya moleküler makineler gibi doğal biyolojik makromoleküllere de uygulanır.

<span class="mw-page-title-main">Plastik enjeksiyon</span>

Plastik enjeksiyon, temelde kapalı bir kalıbın içine plastik malzemenin eriyik sıcaklığının üstündeki bir sıcaklık aralığında yüksek hızda yolluk girişinden kalıp gözüne hızlı bir şekilde enjekte edilmesi sonrası, ütüleme fazı ve tutma fazı ile parçanın boyut ve görsel toleranslarının kabul edilebilir seviyeye getirdikten sonra plastiğin kalıptan çıkma sıcaklığının altına getirilerek kalıptan çıkarılması prensibine dayanan bir plastik parça imalat yöntemidir. Seri üretime uygun olması sebebiyle, birçok sektörde oldukça fazla kullanılan bir üretim yöntemidir. Bu metot ile en küçük komponentlerden, otomotiv, savunma sanayi ürünlerine kadar çok çeşitli ebat ve kategorilerde plastik parçalar imal edilebilir.

<span class="mw-page-title-main">Kojenerasyon</span>

Kojenerasyon, tercihen ısı tüketimi olan yerlerde kullanılan ve aynı zamanda bölge ısıtma ağını yararlı ısıyla besleyebilen elektrik enerjisi ve ısı üretebilen modüler yapılı bir sistemdir. Bu sistem kombine ısı ve güç sistemi ilkesine dayanmaktadır.

Termodinamiğin(Isıldevinimin) ikinci yasası, izole sistemlerin entropisinin asla azalamayacağını belirtir. Bunun sebebini izole sistemlerin termodinamik dengeden spontane olarak oluşmasıyla açıklar. Buna benzer olarak sürekli çalışan makinelerin ikinci kanunu imkânsızdır.

<span class="mw-page-title-main">Küme</span> matematiksel anlamda tanımsız bir kavramdır. Bu kavram "nesneler topluluğu veya yığını" olarak yorumlanabilir.

Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.

<span class="mw-page-title-main">Sonsuz</span> matematik ve fizikte herhangi bir sonu olmayan şeyler ve sayılar

Sonsuz, eski Yunanca Lemniscate kelimesinden gelmektedir, çoğunlukla matematik ve fizikte herhangi bir sonu olmayan şeyleri ve sayıları tarif etmekte kullanılan soyut bir kavramdır.

<span class="mw-page-title-main">Termodinamik kanunları</span>

Termodinamik yasaları, termodinamiğin temelini oluşturan dört yasadır. Termodinamik proseslerdeki ısı ve iş transferlerinin yapısını tanımlar.

Bulanık küme kavramı, küme kavramının eleman olmanın derecelendirilmesine dayanan bir genelleştirilmesidir. Bulanık kümeler belirtisiz mantığın doğal bir genişlemesi olarak 1965 yılında Lütfi Aliaskerzade tarafından tanımlanmıştır. Bir nesne bir kümenin ya elemanı ya da elemanı değilken, bir bulanık kümenin belirli bir oranda kısmen elemanı olabilir.

Sonsuz küçükler, ölçülemeyecek kadar küçük cisimleri tarif etmek için kullanılır. Sonsuz küçüklerden yararlanmaktaki asıl amaç nicelik bakımından çok küçük olsalar da hala açı, eğim gibi belirli özelliklere sahip olmalarıdır. Sonsuz küçük kelimesi 17. Yüzyıl Modern Latin uydurma sözcüğü olan bir dizideki “sonsuzuncu” terim anlamına gelen infitesimustan gelmektedir. İlk olarak 1670 yılı civarında Nicolas Marecator ya da Gottfried Wilhelm Leibniz tarafından kullanılmıştır. Genel anlamla sonsuz küçük bir cisim herhangi bir uygulanabilir ölçümden küçük olan ama boyut olarak sıfırdan farklı ya da çok küçük olan ve bu nedenle sıfırdan ayırt edilemeyecek durumdaki cisimdir. Bundan dolayı sonsuz küçük ifadesi sıfat olarak kullanıldığında aşırı derecede küçük anlamına gelmektedir. Bir anlam verebilmek için genellikle aynı bağlamdaki başka bir sonsuz küçük ile karşılaştırılması gerekir. Sonsuz miktarda çok sonsuz küçük bir integral üretmek amacıyla toplanır. Arşimet “Mekanik Teoremlerin Metodu” adı verilen çalışmasında katı cisimlerin hacimlerini ve bölgelerin alanlarını bulmak için Bölünmezler Yöntemi olarak bilinen yöntemi kullanmıştır. Yayımlanan resmi bilimsel eserlerinde aynı problemleri Tüketme Yöntemi ile çözmüştür. 15. Yüzyılda Cusalı Nicholas’ın üzerinde çalıştığı bir çemberin alanını çemberi sonsuz kenarlı bir çokgen olarak hesaplama yöntemi 17. Yüzyılda Johannes Kepler tarafından geliştirilmiştir. Simon Stevin’in 16. Yüzyılda tüm sayıların ondalık gösterimi üzerine yaptığı çalışmalar gerçek sürekliliğe temel hazırladı. Bonaventura Cavalieri’nin bölünmezler yöntemi klasik yazarların sonuçlarını genişletmesine olanak sağladı. Bölünmezler yöntemi, eş boyutlu varlıklardan oluşan geometrik figürler ile ilişkilidir. John Wallis’in sonsuz küçük görüşü geometrik figürleri figürle aynı boyuta sahip sonsuz yapı bloğuna bölmesi ile bölünmezler yönteminden ayrılır. Bu görüş integral kalkülüsünün genel yöntemleri için temel hazırlamıştır. Sonsuz küçükleri alan hesabında ile göstermiştir. Leibniz tarafından kullanılan sonsuz küçükler, sonlu ve sonsuz sayılar için başarılı olan Süreklilik Kuramı ve belirlenemez miktarlar için gösterimi değiştirmenin yönteminin sadece belirlenebilir olanları göstererek yapılacağını anlatan Aşkın Homojenite Yasası gibi bulgusal prensiplere dayanmaktaydı. 18. Yüzyıl sonsuz küçüklerin Leonard Euler ve Joseph-Louis Lagrange gibi matematikçiler tarafından sıklıkla kullanıldığı bir zaman aralığı olmuştur. Augustin-Louis Cauchy sonsuz küçükleri Cour d’Analyse adlı eserinde sürekliliği açıklamak için ve Dirac delta fonksiyonunun ilk formlarından birini tanımlarken kullanmıştır. Tıpkı Cantor ve Dedekind’ın Stevin’in sürekliliğinin daha soyut bir halini geliştirdikleri gibi Paul du Bois-Reymond da sonsuz küçük ile zenginleştirilmiş süreklilik üzerine fonksiyonların artış oranını temel alan bir seri çalışma yapmıştır. Du Bois-Reymond’un çalışması Emile Boral ve Thoralf Skolem’ e ilham verdi. Borel Bois-Reymond’un çalışmalarını Cauchy’nin sonsuz küçüklerin artış oranına dair çalışmalarıyla bağlantı kurdu. Skolem 1934’te aritmetiğin standart dışı ilk modellerini geliştirdi. Süreklilik ve sonsuz küçük yasalarının matematiksel “implementasyonu” Abraham Robinson tarafından 1961’de yapılmıştır. Robinson ayrıca Edwin Hewirr’in 1948’de ve Jerzy Łoś’un 1955’teki çalışmalarına dayanarak standart dışı analizi geliştirmiştir. Hipergerçekler sonsuz küçük ile zenginleştirilmiş sürekliliği sağlar ve transfer prensibi de Leibniz’in süreklilik yasasını sağlar.

<span class="mw-page-title-main">Açık yıldız kümesi</span>

Açık yıldız kümeleri, birkaç bin yıldızdan oluşan bir yıldız grubudur. Açık yıldız kümesini oluşturan yıldızlar aynı dev moleküler buluttan oluşmuşlardır ve yaklaşık olarak aynı yaştadırlar. Açık yıldız kümesi galaktik küme olarak da bilinir. Samanyolu Galaksisi'nde 1100'den fazla açık yıldız kümesi keşfedilmiştir ve daha fazla olduğu düşünülmektedir. Açık yıldız kümeleri karşılıklı yerçekimi etkisiyle birbirlerine gevşek bir biçimde bağlıdırlar. Açık yıldız kümeleri diğer kümelerle ve gaz bulutlarıyla yakın temaslarda bulunarak bozulmuş hale gelirler. Bu bozulmalar hem galaksinin ana bölümüne doğru yer değiştirmelere hem de küme elemanlarının yakın temasların içine doğru kaybıyla sonuçlanır.

Uyarlamalı ağ tabanlı bulanık çıkarım sistemi, Takagi-Sugeno bulanık çıkarım sistemine dayalı bir tür yapay sinir ağı yöntemi. Jang tarafından 1990’ların başlarında geliştirilmiş olup doğrusal olmayan fonksiyonların modellenmesinde ve kaotik zaman serilerinin tahmininde kullanılmıştır.

<span class="mw-page-title-main">Set teorisi</span>

Makalenin kısa özeti; farklı nesnelerin koleksiyonları olarak kümeler hakkında konuşur, matematikte birçok kullanımları olduğunu ve matematiğin set teorisinde kodlanabileceğini ve matematiğin çoğunu yapmak için yeterince küme teorisinin aksiyomatize edilebileceğini belirtir. Konunun aksiyomları veya amaçlanan yorumu ile tanımlanıp tanımlanmadığı konusunda tarafsız kalır. Antinomilerden bahsedilirse, aksiyomatizasyonun çözüm olduğunu iddia etmemeli, ancak bazılarının onları aksiyomatizasyon ile çözüldüğünü, diğerleri de kümülatif hiyerarşi ile değerlendirdiğini belirtmelidir. -> Venn diyagramı, ikisinin set matematik Kümeleri. Küme teorisi, gayri resmi olarak nesne koleksiyonları olan matematiksel mantığın ' kümeleri üzerinde çalışan bir dalıdır. Herhangi bir nesne türü bir kümede toplanabilse de, küme teorisi çoğunlukla matematikle ilgili nesnelere uygulanır. Küme teorisinin dili neredeyse tüm matematiksel nesne leri tanımlamak için kullanılabilir.

Bulanık matematik ; matematiğin bulanık mantığın bulanık kümeler teorisini inceleyen dalıdır.

Adaptif rezonans teorisi (ART), Stephen Grossberg ve Gail Carpenter tarafından beynin bilgiyi nasıl işlediğini anlamak üzere geliştirilen bir teoridir. Denetimli ve denetimsiz öğrenme yöntemlerini kullanan ve örüntü tanıma ve tahmin gibi sorunları ele alan bir dizi sinir ağı modelini açıklamaktadır.


Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.