Birim küre

Birim küre, belirli merkez noktasından 1 birim uzaklıkta olan noktalar kümesidir.Mesafelerin genellenmiş kavramları olarak da kullanılabilir.Kapalı bir birim küre,merkezden 1 birim az veya 1 birime eşit uzaklıktaki noktalar kümesidir.Genellikle,boşluktaki orijinden bir nokta ayırt edilmişitir ve bu noktanın birim kürenin veya birim topun merkezi olduğu anlaşılır.Bu yüzden birim küre ya da birim topun aynı olduğu söylenir. Örneğin;bir boyutlu küre,genellikle bir halka olarak adlandırılan bir yüzeydir ve çember bir içi yüzeye ve dış yüzeye sahipse iki boyutlu bir küredir.Benzer bir şekilde,halk dilinde küre olarak bilinen Öklid katısının yüzeyi iki boyutlu küredir ve ayrıca içi ve dış yüzeye sahip olduğunda üç boyutlu küre olur. Bir birim küre basitçe bir küre yarıçapına sahiptir.Birim kürenin önemi,herhangi bir kürenin ölçeklendirme ve çevirme kombinasyonlarına dönüşebilmesinden anlayabiliriz.Bu yolla,çalışırken kürenin temel özelliklerini daha aza indirgeyebiliriz.

Öklid uzayında n boyutunda,birim küre aşağıdaki denklemi sağlayan noktalar ${\displaystyle (x_{1},\ldots ,x_{n})}$ kümesidir.

${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}=1}$

Ve kapalı birim top,aşağıdaki eşitsizliği sağlayan noktalar kümesidir.

${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}\leq 1.}$

Yarıçapı 1 birim olan ve x-, y- ve z- eksenlerinde değişikliğe sahip olmayan elipsoid birim kürenin klasik denklemini verir.

${\displaystyle f(x,y,z)=x^{2}+y^{2}+z^{2}=1}$

Öklid uzayında n boyutunda bir birim kürenin hacmi ve birim kürenin yüzey alanı birçok önemli formülde karşımıza çıkabilir.n boyutlu bir kürenin hacmini V_n olarak gösteririz,bu gama fonksiyonu kullanarak açıklanabilir.

${\displaystyle V_{n}={\frac {\pi ^{n/2}}{\Gamma (1+n/2)}}={\begin{cases}{\pi ^{n/2}}/{(n/2)!}&\mathrm {if~} n\geq 0\mathrm {~is~even,} \\~\\{\pi ^{\lfloor n/2\rfloor }2^{\lceil n/2\rceil }}/{n!!}&\mathrm {if~} n\geq 0\mathrm {~is~odd,} \end{cases}}}$

n!! double faktöriyel demektir. (n-1) boyutlu birim kürenin hiperhacmi (n boyutta bir topun yüzey alanı gibi) A_n ile gösterilir ve alttaki formülle açıklanabilr;

${\displaystyle A_{n}=nV_{n}={\frac {n\pi ^{n/2}}{\Gamma (1+n/2)}}={\frac {2\pi ^{n/2}}{\Gamma (n/2)}}\,,}$

Son eşitlikte n > 0 olan değerler için kullanılabilr. Bazı ${\displaystyle n}$ değerleri için bazı yüzey alanlar ve hacimleri;

${\displaystyle n}$	${\displaystyle A_{n}}$ (yüzey alan)		${\displaystyle V_{n}}$ (hacim)
0	${\displaystyle 0(1/0!)\pi ^{0}}$	0	${\displaystyle (1/0!)\pi ^{0}}$	1
1	${\displaystyle 1(2^{1}/1!!)\pi ^{0}}$	2	${\displaystyle (2^{1}/1!!)\pi ^{0}}$	2
2	${\displaystyle 2(1/1!)\pi ^{1}=2\pi }$	6.283	${\displaystyle (1/1!)\pi ^{1}=\pi }$	3.141
3	${\displaystyle 3(2^{2}/3!!)\pi ^{1}=4\pi }$	12.57	${\displaystyle (2^{2}/3!!)\pi ^{1}=(4/3)\pi }$	4.189
4	${\displaystyle 4(1/2!)\pi ^{2}=2\pi ^{2}}$	19.74	${\displaystyle (1/2!)\pi ^{2}=(1/2)\pi ^{2}}$	4.935
5	${\displaystyle 5(2^{3}/5!!)\pi ^{2}=(8/3)\pi ^{2}}$	26.32	${\displaystyle (2^{3}/5!!)\pi ^{2}=(8/15)\pi ^{2}}$	5.264
6	${\displaystyle 6(1/3!)\pi ^{3}=\pi ^{3}}$	31.01	${\displaystyle (1/3!)\pi ^{3}=(1/6)\pi ^{3}}$	5.168
7	${\displaystyle 7(2^{4}/7!!)\pi ^{3}=(16/15)\pi ^{3}}$	33.07	${\displaystyle (2^{4}/7!!)\pi ^{3}=(16/105)\pi ^{3}}$	4.725
8	${\displaystyle 8(1/4!)\pi ^{4}=(1/3)\pi ^{4}}$	32.47	${\displaystyle (1/4!)\pi ^{4}=(1/24)\pi ^{4}}$	4.059
9	${\displaystyle 9(2^{5}/9!!)\pi ^{4}=(32/105)\pi ^{4}}$	29.69	${\displaystyle (2^{5}/9!!)\pi ^{4}=(32/945)\pi ^{4}}$	3.299
10	${\displaystyle 10(1/5!)\pi ^{5}=(1/12)\pi ^{5}}$	25.50	${\displaystyle (1/5!)\pi ^{5}=(1/120)\pi ^{5}}$	2.550

n ≥ 2 için genişletilmiş ondalık değerleri hassas olarak yuvarlanır.

A_n değerleri tekrarlamayı karşılar,

${\displaystyle A_{0}=0}$

${\displaystyle A_{1}=2}$

${\displaystyle A_{2}=2\pi }$

${\displaystyle A_{n}={\frac {2\pi }{n-2}}A_{n-2}}$ for ${\displaystyle n>2}$.

V_n değerleri tekrarlamayı karşılar,

${\displaystyle V_{0}=1}$

${\displaystyle V_{1}=2}$

${\displaystyle V_{n}={\frac {2\pi }{n}}V_{n-2}}$ for ${\displaystyle n>1}$.

A_n ve V_n herhangi bir gerçek sayın ≥ 0, için hesaplanabilir. n 0 olmayan bir tam sayı olduğunda kürenin alanını veya topun hacmini saklamak için uygun koşullar vardır.

Yarıçapı r olan (n–1) boyutlu bir kürenin yüzey alanı A_n rⁿ⁻¹ ve yarıçapı r olan n boyutlu bir topun hacmi V_n rⁿ. For instance, the area is {{Kayma|A =.Örneğin,yarıçapı r olan üç boyutlu topun yüzey alanı A = 4π r²’dir.Yarıçapı r olan üç boyutlu bir topun hacmi ise V = 4π r³ / 3 ‘dir.

Normlu bir uzayda ${\displaystyle V}$,norm’la ${\displaystyle \|\cdot \|}$, birlikte açık birim top,aşağıdaki bağıntıyı verir;

${\displaystyle \{x\in V:\|x\|<1\}.}$

Kapalı birim topun içi; (V,||•||),

${\displaystyle \{x\in V:\|x\|\leq 1\}.}$

Birim küre ayrık ve ortak sınırlara sahip;birim küre (V,||•||),

${\displaystyle \{x\in V:\|x\|=1\}.}$

Birim topun şekli tamamen seçilen norma bağlıdır.İyi köşelere sahip olabilir ve [−1,1] gibi görülebilir ve norm ⁿ,durumunda l_∞ in Rⁿ.Normal yuvarlak bir top genellikle Hilbert spacenormu üzerinde sonlu-boyutlu Öklid mesafesi üzerinde anlaşılır.Sınırladığı alan birim kürenin genellikle hangi anlama geldiğini tanımlar.p çeşitli değerlerinde,birim topun iki boyutlu uzayı${\displaystyle \ell ^{p}}$ space için burada bazı fotoğraflar vardır.(birim top konkav olduğunda p < 1,konveks olduğunda p ≥ 1):

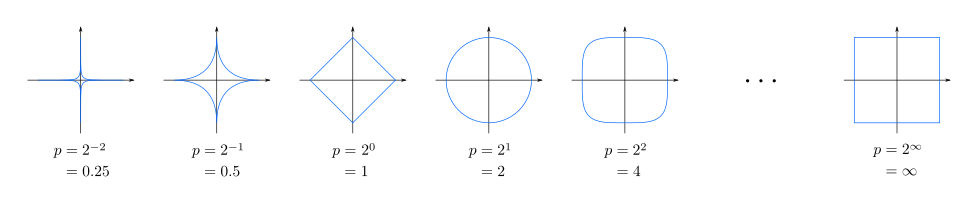
Bu nedenle bu durump ≥ 1 göstermektedir. İki boyutlu birim topların çevreleri${\displaystyle C_{p}}$;

${\displaystyle C_{0}=C_{\infty }=8}$ maximum değerdir.

${\displaystyle C_{1}=4{\sqrt {2}}}$ minimum değerdir.

${\displaystyle C_{2}=2\pi \,.}$

Yukarıda tanımlanan her üç doğrudan, seçilen orijine göre bir metrik uzay açıkça genelleştirilebilir.Ancak,topolojik düşünceler(iç,kapatma,sınır) aynı yola (ultrametric alanlarda,açık kapalı kümelerin tümü)başvurmaya ihtiyaç duymaz ve birim küre bazı metrik uzaylarda boş bile olabilir.

Eğer V gerçek olan bir doğrusal uzayın kuadratik form’u F:V → R,daha sonra { p ∈ V : F(p) = 1 } birim küre ya da Vnin birim yarı küresidir denebilir.Örneğin;kuadrik formu ${\displaystyle x^{2}-y^{2}}$,,birine eşit ayarlandığında bölünmüş karmaşık sayılar düzleminde birim çember rolünü oynayan birim hiperbol oluşturulur.Kuadratik formu x² uzayın içinde birim küre için bir çizgi çifti oluşturur.