
Matematikte türev, bir fonksiyonun tanımlı olduğu herhangi bir noktada değişim yönünü veya hızını veren temel bir kavramdır. Tek değişkenli bir fonksiyonun tanım kümesinin belli bir noktasında türevi, fonksiyonun grafiğine bu noktada karşılık gelen değerde çizilen teğet doğrunun eğimidir. Teğet doğru, tanım kümesinin bu noktasında fonksiyonun en iyi doğrusal yaklaşımıdır. Bu nedenle türev genellikle anlık değişim oranı ya da daha açık bir ifadeyle, bağımlı değişkendeki anlık değişimin bağımsız değişkendeki anlık değişime oranı olarak tanımlanır. Bir fonksiyonun türevini teorik olarak bulmaya türev alma denilir. Eğer bir fonksiyonun tanım kümesindeki her değerinde hesaplanan türev değerlerini veren başka bir fonksiyon varsa, bu fonksiyona eldeki fonksiyonun türevi denir.

İntegral veya tümlev, toplama işleminin sürekli bir aralıkta alınan hâlidir. Türev ile birlikte kalkülüsün temelini oluşturan iki işlemden birisidir. Kalkülüsün temel teoremi sayesinde aynı zamanda türevin ters işlemidir.

Limit kelimesi Latince Limes ya da Limites 'den gelmekte olup sınır, uç nokta anlamındadır. Öklid ve Arşimet tarafından eğrisel kenarlara sahip şekillerle ilgili olan teoremlerde kullanılmıştır. Limit kavramı, çok önceleri kullanılmasına rağmen sonra unutulmuş ve daha sonra Newton ile Leibniz'in eserlerinde görülmüştür. Mesela, diferansiyel hesapta bir eğri sonsuz küçük uzunlukta sonsuz kenara sahip bir çokgen olarak kabul edilir. Limit kavramından ortaya çıkan diferansiyel hesap, pek çok fizik probleminin kolayca ele alınmasını sağlar.

Taylor serisi matematikte, bir fonksiyonun, o fonksiyonun terimlerinin tek bir noktadaki türev değerlerinden hesaplanan sonsuz toplamı şeklinde yazılması şeklindeki gösterimi/açılımıdır. Adını İngiliz matematikçi Brook Taylor'dan almıştır. Eğer seri sıfır merkezli ise, Taylor serisi daha basit bir biçime girer ve bu özel seriye İskoç matematikçi Colin Maclaurin'e istinaden Maclaurin serisi denir. Bir serinin terimlerinden sonlu bir sayı kadarını kullanmak, bu seriyi bir fonksiyona yakınsamak için genel bir yöntemdir. Taylor serisi, Taylor polinomunun limiti olarak da görülebilir.

Normal dağılım, aynı zamanda Gauss dağılımı veya Gauss tipi dağılım olarak isimlendirilen, birçok alanda pratik uygulaması olan, çok önemli bir sürekli olasılık dağılım ailesidir.

Başlangıçta sonsuz küçük hesap veya "sonsuz küçüklerin hesabı" olarak adlandırılan kalkülüs, geometrinin şekillerle çalışması ve cebirin aritmetik işlemlerin genellemelerinin incelenmesi gibi, kalkülüs sürekli değişimin matematiksel çalışmasıdır.
Matematikte sonuşmaz veya asimptot, belirli bir A eğrisine istenildiği kadar yaklaşabilen ikinci bir B eğrisine verilen addır. Bir başka deyişle, A üzerinde ilerledikçe, A ve B arasındaki mesafe azalır ve sıfıra yaklaşır. Asimptot kelimesi, Yunanca "beraber düşmek" anlamındaki simpiptein fiilinin olumsuz halinden türemiştir.
Merkezi limit teoremi büyük bir sayıda olan bağımsız ve aynı dağılım gösteren rassal değişkenlerin aritmetik ortalamasının, yaklaşık olarak normal dağılım göstereceğini ifade eden bir teoremdir. Matematiksel bir ifadeyle, bir merkezi limit teoremi olasılık kuramı içinde bulunan bir zayıf yakınsama sonucu setidir. Bunların hepsi, birçok bağımsız aynı dağılım gösteren rassal değişkenlerin herhangi bir toplam değerinin limitte belirli bir "çekim gücü gösteren dağılıma" göre dağılım gösterme eğiliminde olduğu gerçeğini önerir.
Bir olasılık dağılımı bir rassal olayın ortaya çıkabilmesi için değerleri ve olasılıkları tanımlar. Değerler olay için mümkün olan tüm sonuçları kapsamalıdır ve olasılıkların toplamı bire eşit olmalıdır. Örneğin, bir rassal olay olarak madeni paranın tek bir defa havaya atılıp yere düşmesi ele alınsın; değerler 'yazı' veya 'tura' veya bunlar isimsel değişken ölçeğinde ifade edilirse 0 (yazı) veya 1 (tura) olur; olasılıklar ise her iki değer için ½ olacaktır. Böylece madeni bir paranın tek bir defa atılma olayı için iki değer ve ilişkili iki olasılık bu rassal olayın olasılık dağılımı olur. Bu dağılım ayrık olasılık dağılımıdır; çünkü sayılabilir şekilde ayrı ayrı sonuçlar ve bunlara bağlı olan pozitif olasılıklar vardır.

Olasılık kuramı bilim dalında bir olasılık kütle fonksiyonu bir ayrık rassal değişkenin olasılığının tıpatıp belli bir değere eşit olduğunu gösteren bir fonksiyondur. Olasılık kütle fonksiyonu, olasılık yoğunluk fonksiyonundan farklıdır; çünkü olasılık yoğunluk fonksiyonu yalnızca sürekli rassal değişkenler için tanımlanmış olup doğrudan doğruya olasılık değerini vermezler. Olasılık yoğunluk fonksiyonunun bir belli değer aralığı için integrali alınırsa bu rassal değişkenin belirlenen değer aralığı için olasılığını verir.
Olasılık kuramı içinde herhangi bir rassal değişken için karakteristik fonksiyon, bu değişkenin olasılık dağılımını tüm olarak tanımlar. Herhangi bir rassal değişken X için, gerçel doğru üzerinde, bu fonksiyonu tanımlayan formül şöyle yazılır:


Matematiğin matematiksel fizik alanında ve rassal süreçler teorisinde bir harmonik fonksiyon, Rn'nin U gibi açık bir kümesi üzerinde f : U → R şeklinde tanımlı, Laplace denklemini, yani

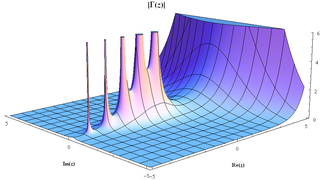
Meromorf fonksiyon, özellikle karmaşık analizde, bir fonksiyon çeşidi. Daha açık bir ifadeyle, meromorf fonksiyon, karmaşık düzlemin açık bir D kümesi üzerinde fonksiyonun kutup noktalarından oluşan belli bir korunmalı noktalar kümesi haricinde D 'nin geriye kalan diğer noktalarının tümünde holomorf olan fonksiyondur. Meromorf kelimesi Yunanca "kısım", "parça" anlamına gelen “meros” ve "tüm", "bütün" anlamına gelen “holos” kelimelerinin tezat bir birleşiminden ortaya çıkmış bir kelimedir.
Matematiğin bir alt dalı olan karmaşık analizde Hurwitz teoremi, matematikçi Adolf Hurwitz'in ispatladığı ve bu yüzden onun ismini almış önemli bir sonuçtur. Genel bir şekilde ifade etmek gerekirse, Hurwitz teoremi karmaşık düzlemdeki bir bölge üzerinde tanımlı bir holomorf fonksiyonlar dizisinin sıfırları ile bu dizinin limiti olan fonksiyonun sıfırlarını ilişkilendirir.
Matematiğin bir alt dalı olan karmaşık analizde, holomorf bir f fonksiyonunun sıfırı veya kökü f(a) = 0 eşitliğini sayılan karmaşık a sayısına verilen bir addır. Başka bir deyişle, holomorf fonksiyonların sıfır değerini aldığı karmaşık sayılara o fonksiyonun sıfırları adı verilir.

Matematikte bir doğrunun eğimi ya da gradyanı o doğrunun dikliğini, eğimliliğini belirtir. Daha büyük eğim, daha dik bir doğru demektir.
Sonlu fark, f(x + b) − f(x + a) matematiksel ifadesidir.
Matematikte bir fonksiyonun limiti, kalkülüs ve analizde kullanılan bir temel kavramdır ve belirli bir girişe yaklaşan bir fonksiyonun davranışı ile ilgilidir.
Kalkülüs ve matematiksel analizin diğer dallarında cebirsel işlemlerle ilgili olan limitler, daha çok alt ifadelerin yer değiştirmesi ile gerçekleştirilir. Bu değişimden sonra elde edilen ifade eğer, asıl limit ile ilgili yeteri kadar bilgi içermiyorsa, buna 'belirsiz form denir.

Kalkülüste, Rolle teoremi veya Rolle lemması temel olarak, iki farklı noktada eşit değerlere sahip herhangi bir gerçel değerli türevlenebilir fonksiyonun, aralarında bir yerde, teğet doğrusunun eğiminin sıfır olduğu en az bir noktaya sahip olması gerektiğini belirtir. Böyle bir nokta, durağan nokta olarak bilinir. Bu nokta, fonksiyonun birinci türevinin sıfır olduğu noktadır. Teorem adını Michel Rolle'den almıştır.



















