
Ekonometri İki veya daha fazla verinin, birbirleri arasındaki ilişkiyi ve bu ilişkiden yola çıkarak, matematik, istatistik ve bilgisayar bilimi aracılığıyla ekonomik ilişkilerin ampirik bir biçimde değerlendirilerek, bu veriler arasındaki ilişkiyi inceleyen bilim dalıdır. Daha açık olmak gerekirse, "sonucu uygun metodlarla ilişkilendirilmiş, teori ve gözlemin eşzamanlı gelişimi tabanlı mevcut ekonomik olgunun nicel çözümlemesidir." Bir ekonomiye giriş ders kitabı ekonometriyi: "dağlarca verinin arasından basit ilişkileri çıkarmak için titizlikle araştırmak" olarak açıklamıştır. "Ekonometri" terimi ilk olarak Polonyalı ekonomist Pawel Ciompa tarafından 1910 yılında kullanılmıştır. Bugünkü kullanım şekline getiren ise Ragnar Frisch'dir. Günümüzde daha güçlü bilgisayar yazılımların varlığıyla ekonometrik analizlerin gücü artmıştır.

İstatistik veya sayım bilimi, belirli bir amaç için veri toplama, tablo ve grafiklerle özetleme, sonuçları yorumlama, sonuçların güven derecelerini açıklama, örneklerden elde edilen sonuçları kitle için genelleme, özellikler arasındaki ilişkiyi araştırma, çeşitli konularda geleceğe ilişkin tahmin yapma, deney düzenleme ve gözlem ilkelerini kapsayan bir bilimdir. Belirli bir amaç için verilerin toplanması, sınıflandırılması, çözümlenmesi ve sonuçlarının yorumlanması esasına dayanır. Bu çerçevede yapılan işlemlerin tümüne sayımlama denir.
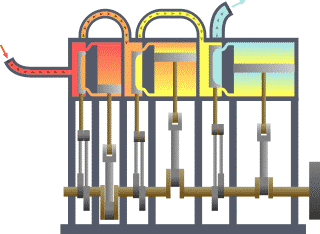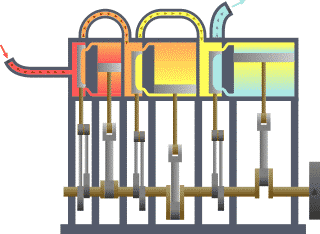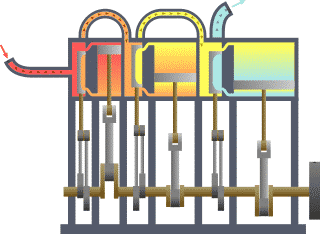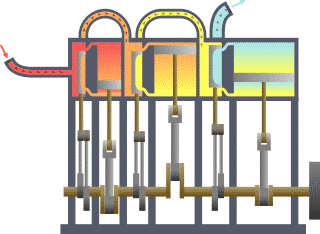
Termodinamik; ısı, iş, sıcaklık ve enerji arasındaki ilişki ile ilgilenen bilim dalıdır. Basit bir ifadeyle termodinamik, enerjinin bir yerden başka bir yere ve bir biçimden başka bir biçime transferi ile ilgilenir. Bu süreçteki anahtar kavram, ısının, belirli bir mekanik işe denk gelen bir enerji biçimi olmasıdır.
Eğitimsel ölçme, genel anlamda ölçme, bir olguya anlamlı sayı ya da semboller atama işlemidir. Eğitsel ölçme ise bu olguların öğrenme ürün ya da sürecine göre kazanımları kapsar. Eğitimsel ölçmelerin amacı ölçülmesi amaçlanan öğrenme yapılarının görgül kestirimlerini sağlamaktır. Bu amaca yönelik olarak değişik ölçme modelleri geliştirilmiştir.
Regresyon analizi, iki ya da daha çok nicel değişken arasındaki ilişkiyi ölçmek için kullanılan analiz metodudur. Eğer tek bir değişken kullanılarak analiz yapılıyorsa buna tek değişkenli regresyon, birden çok değişken kullanılıyorsa çok değişkenli regresyon analizi olarak isimlendirilir. Regresyon analizi ile değişkenler arasındaki ilişkinin varlığı, eğer ilişki var ise bunun gücü hakkında bilgi edinilebilir. Regresyon terimi için öz Türkçe olarak bağlanım sözcüğü kullanılması teklif edilmiş ise de Türk ekonometriciler arasında bu kullanım yaygın değildir.
Korelasyon, olasılık kuramı ve istatistikte iki rassal değişken arasındaki doğrusal ilişkinin yönünü ve gücünü belirtir. Genel istatistiksel kullanımda korelasyon, bağımsızlık durumundan ne kadar uzaklaşıldığını gösterir.
Değişken, bilgisayar ve matematik biliminde sembolik bir ifade veya bir niceliği (miktarı) ifade etmek için kullanılan semboldür. Matematikte, değişken, sık sık bilinmeyen bir niceliğin tanımlanması için; bilgisayar biliminde ise, niceliğin depolanabileceği bir yer, alan ifade eder. Değişkenler, sıklıkla bilinen ve sabit olan değerlerle mukayase edilir.
Matematikte, bir kısmi diferansiyel denklem birkaç değişkenli bir fonksiyon ile bu fonksiyonun değişkenlere göre kısmi türevleri arasındaki ilişkiyi inceler.
Bir olasılık dağılımı bir rassal olayın ortaya çıkabilmesi için değerleri ve olasılıkları tanımlar. Değerler olay için mümkün olan tüm sonuçları kapsamalıdır ve olasılıkların toplamı bire eşit olmalıdır. Örneğin, bir rassal olay olarak madeni paranın tek bir defa havaya atılıp yere düşmesi ele alınsın; değerler 'yazı' veya 'tura' veya bunlar isimsel değişken ölçeğinde ifade edilirse 0 (yazı) veya 1 (tura) olur; olasılıklar ise her iki değer için ½ olacaktır. Böylece madeni bir paranın tek bir defa atılma olayı için iki değer ve ilişkili iki olasılık bu rassal olayın olasılık dağılımı olur. Bu dağılım ayrık olasılık dağılımıdır; çünkü sayılabilir şekilde ayrı ayrı sonuçlar ve bunlara bağlı olan pozitif olasılıklar vardır.
Olasılık teorisi ya da ihtimaliyet teorisi rastgele olayların analizi ile ilgilenen bir matematik bilim dalıdır. Olasılık teorisinin ana ögeleri rassal değişkenler, saf rassal süreçler, olaylar olarak sayılabilir. Bunlar ya tek olarak ortaya çıkan veya bir zaman dönemi içinde gelişerek meydana gelen, ilk görünüşü rastgele bir şekilde olan deterministik olmayan olayların veya ölçülebilir miktarların matematiksel soyutlamalarıdır. Bir madeni parayı yazı-tura denemesi için havaya atmak veya bir zarı atmak ile ortaya çıkan sonuç ilk bakışta rastgele bir olay olarak görülebilirse bile eğer birbirini takip eden rastgele olaylar tekrar tekrar ortaya çıkartılırsa incelenebilecek ve tahmin edilebilecek belirli bir istatistiksel seyir takip ettikleri görülecektir. Bu türlü olaylar ve sonuçların seyirlerini betimleyen iki temsilci matematiksel sonuç büyük sayılar yasası ve merkezsel limit teoremidir.

Doğrusal olmayan regresyon, istatistik bilimde gözlemi yapılan verilerin bir veya birden fazla bağımsız değişkenin model parametrelerinin doğrusal olmayan bileşiği olan ve bir veya daha çok sayıda bağımsız değişken ihtiva eden bir fonksiyonla modelleştirilmesini içeren bir regresyon (bağlanım) analizi türüdür. Veriler arka-arkaya yapılan yaklaşımlarla kurulan modele uydurularak çözümleme yapılır.
Olasılık kuramında iki olayın bağımsız olması bu olaylardan birinin gerçekleşme olasılığının diğer olayın gerçekleşip gerçekleşmediğine bağlı olmaması anlamına gelmektedir. Örneğin;
- Bir zarın ilk atışta 6 gelmesi olayı ile ikinci atışta 6 gelmesi olayı bağımsızdır.
- Öte yandan, bir zarın ilk atışta 6 gelmesi olayı ilk iki atış sonunda elde edilen sayılar toplamının 8 olması olayına bağlıdır.
- Bir kart destesinden seçilen ilk kartın kırmızı olması olayı ile ikinci kartın aynı renkte olması olayı bağımsızdır. Ne var ki, seçilen kartın desteye geri konulmaması durumunda bu iki olay bağımlıdır.
Sinyal (işaret), fiziksel değişkenlerin durumu hakkında bilgi taşıyan ve matematiksel olarak fonksiyon (İşlev) biçiminde gösterilen kavrama denir.
Kısmi regresyon katsayıları çoklu regresyon modellerinde yer alan katsayılardır. Bu katsayıları, bağımsız değişkenler ile bağımlı değişken arasındaki ilişkiyi diğer bağımsız değişkenlerin etkilerini sabit tutarak ortaya koyarlar.
Ki-kare testi veya χ² testi istatistik bilimi içinde bir sıra değişik problemlerde kullanılan bazıları parametrik olmayan sınama ve diğerleri parametrik sınama yöntemidir. Bu çeşit istatistiksel sınamalarda test istatistiği için "örnekleme dağılımı", sıfır hipotez gerçek olursa ki-kare dağılımı gösterir veya sıfır hipotez "asimptotik olarak gerçek" olursa, eğer sıfır hipotez gerçekse ve eğer örnekleme hacmi istenilen kadar yeterli olarak büyük ise bir ki-kare dağılımına çok yakın olarak yaklaşım gösterir.
Pearson ki-kare testi nicel veya nitel değişkenler arasında bağımlılık olup olmadığının, örnek sonuçlarının belirli bir teorik olasılık dağılımına uygun olup olmadığının, iki veya daha fazla örneğin aynı anakütleden gelip gelmediğinin, ikiden fazla anakütle oranının birbirine eşit olup olmadığının ve çeşitli anakütle oranlarının belirli değere eşit olup olmadığının araştırılmasında kullanılır. İstatistik biliminin çıkarımsal istatistik bölümünde ele alınan iki-değişirli parametrik olmayan test analizlerinden olan ve ki-kare dağılımı'nı esas olarak kullanan ki-kare testlerinden en çok kullanılanıdır. İngiliz istatistikçi olan Karl Pearson tarafından 1900'da ortaya çıkartılmıştır.

Çizelge, birbirine bağlanan düz çizgi parçalarının veri noktaları serisinin bilgisini gösteren bir tür çizimdir. Çizelge genellikle belirli bir zaman aralığındaki - zaman serisi - verilerin değerlerini görselleştirmek için kullanılır ve kronolojiksel olarak çizilir. Bazen sıcaklık ölçümü için de kullanılır.

Parametre belirli bir sistemi tanımlamak veya sınıflandırmak için yardımcı olabilecek herhangi bir özellik. Parametre, sistemi tanımlarken veya performansını, durumunu değerlendirirken yararlı veya kritik olan bir sistem unsurudur.

Matematiksel istatistik, istatistiksel veri toplama tekniklerinin aksine, matematiğin bir dalı olan olasılık teorisinin istatistiğe uygulanmasıdır. Bunun için kullanılan özel matematiksel teknikler arasında matematiksel analiz, doğrusal cebir, stokastik analiz, diferansiyel denklemler ve ölçü teorisi bulunur.

Ekonomide kullanılan ölçüler, fiziksel ölçüler, nominal fiyat değer ölçüleri ve sabit fiyat değer ölçüleridir. Bu ölçümler, ölçtükleri değişkenler ve ölçümlerin dışında bırakılan değişkenler açısından birbirinden farklılık gösterir. Ekonomide ölçülebilir değişkenler nicelik, nitelik ve dağıtımdır. Değişkenlerin ölçümden çıkarılması, ölçümün belirli bir değişkene daha iyi odaklanmasını mümkün kılar, ancak bu daha dar bir yaklaşım anlamına gelir. Tablo, temel ölçüm türlerini karşılaştırmak için derlenmiştir. İlk sütun ölçüm türlerini, ikincisi ölçülen değişkenleri ve üçüncü sütun ölçüm dışı bırakılan değişkenleri gösterir.







