Aritmetik


Aritmetik; matematiğin sayılar arasındaki ilişkiler ile sayıların problem çözmede kullanımı ile ilgilenen dalı.[1] Aritmetik kavramı ile genellikle sayılar teorisi, ölçme ve hesaplama (toplama, çıkarma, çarpma, bölme, üs alma, kök alma) kastedilir.[1] Bununla birlikte bazı matematikçiler daha karmaşık çeşitli işlemleri de aritmetik başlığı altında değerlendirirler.[1]
Aritmetik sistemler, işlem yapılan sayıların türüne göre çeşitlenir. Tam sayı aritmetiği sadece pozitif ve negatif doğal sayılar ile yapılan hesaplamaları içerirken, rasyonel sayı aritmetiği, tam sayılar arasındaki kesirlerle yapılan işlemleri kapsar. Reel sayı aritmetiği, rasyonel ve irrasyonel sayıların her ikisiyle yapılan hesaplamaları barındırır ve tam bir sayı doğrusunu kapsar.
Sistemlerin ayrımı, kullanılan sayı sistemine göre de yapılır. Ondalık aritmetik, en yaygın kullanılan sistemdir ve sayıları ifade etmek için 0'dan 9'a kadar olan temel rakamları ve bu rakamların kombinasyonlarını kullanır. Öte yandan, çoğunlukla bilgisayarlar tarafından kullanılan ikili aritmetik, sayıları 0 ve 1 rakamlarının kombinasyonları olarak temsil eder. Bazı aritmetik sistemler ise sayılardan farklı matematiksel nesneler üzerinde işlem yapar, örneğin aralık aritmetiği ve matris aritmetiği gibi.
Aritmetik işlemler, matematiğin birçok alt dalında, örneğin cebir, kalkülüs ve istatistik gibi alanlarda temel oluşturur. Ayrıca, fizik ve ekonomi gibi bilimlerde de benzer bir işlev görür. Aritmetik, günlük yaşamın birçok yönünde, alışveriş yaparken para üstü hesaplamak veya kişisel finans yönetimi gibi faaliyetlerde kullanılır. Öğrencilerin ilk karşılaştığı matematik eğitimi biçimlerinden biri olan aritmetiğin, bilişsel ve kavramsal temelleri psikoloji ve felsefe tarafından incelenmektedir.
Aritmetiğin pratiği, binlerce hatta belki de on binlerce yıl öncesine uzanmaktadır. Antik uygarlıklar arasında yer alan Mısırlılar ve Sümerliler, M.Ö. 3000 civarında pratik aritmetik sorunları çözmek amacıyla sayı sistemleri geliştirdiler. M.Ö. 7. ve 6. yüzyıllarda, antik Yunanlılar sayılar üzerine daha soyut bir inceleme başlatmış ve katı matematiksel kanıt yöntemlerini tanıtmışlardır. Antik Hindular, sıfır kavramını ve ondalık sistemi ortaya çıkardılar; bu sistem, Orta Çağ'da Arap matematikçiler tarafından geliştirilmiş ve Batı dünyasına aktarılmıştır. İlk mekanik hesap makineleri 17. yüzyılda icat edilmiştir. 18. ve 19. yüzyıllarda, modern sayı teorisinin geliştirilmesi ve aritmetiğin aksiyomatik temellerinin oluşturulması yaşanmıştır. 20. yüzyılda, elektronik hesap makinelerin ve bilgisayarların ortaya çıkışı, aritmetik hesaplamaların doğruluk ve hızını köklü bir şekilde değiştirmiştir. Bu teknolojik ilerlemeler, aritmetik işlemlerin uygulama alanlarını genişleterek, matematik eğitimi ve günlük matematik uygulamalarında önemli dönüşümler yaratmıştır.
Tanım ve etimoloji
Aritmetik, sayılar ve onların işlemleri üzerine çalışan matematiğin temel bir dalıdır. Bu disiplin, toplama, çıkarma, çarpma ve bölme işlemleri aracılığıyla sayısal hesaplamalar yapılmasını içerir.[2] Geniş bir perspektiften bakıldığında, üs alma ve logaritma gibi işlemleri de kapsar.[3]Türkçeye Fransızcadan geçen[4] "aritmetik" terimi, Latince arithmetica kelimesinden türetilmiş olup, bu kelime Antik Yunanca ἀριθμός (arithmos), yani "sayı" ve ἀριθμητική τέχνη (arithmetike tekhne), yani "sayma sanatı" anlamına gelmektedir.[5]
Tanımı konusunda farklı görüşler bulunmaktadır. Dar bir tanımlamaya göre, aritmetik yalnızca doğal sayılar ile ilgilenir.[6] Ancak daha yaygın görüş, kapsamına tam sayılar, rasyonel sayılar, reel sayılar ve bazen de karmaşık sayılar üzerindeki işlemleri dahil etmektir.[2] Bazı tanımlar, aritmetiği yalnızca sayısal hesaplamalar alanına sınırlar.[7] Daha geniş anlamda ele alındığında, sayı kavramının nasıl geliştiğini, sayıların özellikleri ve aralarındaki ilişkilerin analizini ve aritmetik işlemlerin aksiyomatik yapısının incelenmesini de içerir.[8]
Aritmetik, sayı teorisi ile yakından ilişkilidir ve bu alanlar bazen eşanlamlı olarak kullanılsa da,[9] sayı teorisi daha çok tam sayıların özellikleri ve ilişkileri, örneğin bölünebilirlik, faktörizasyon ve asallık gibi konular üzerinde yoğunlaşır[10] ve geleneksel olarak yüksek aritmetik olarak adlandırılır.[11]
Sayılar
Sayılar, miktar ölçümü ve büyüklük değerlendirmesi yapmak için kullanılan temel matematiksel nesnelerdir. Aritmetikte merkezi bir yere sahip olan sayılar, aritmetik işlemlerin tümünün üzerinde yürütüldüğü temel elemanlardır. Sayılar farklı kategorilere ayrılır ve bu sayıları temsil etmek için çeşitli sayısal sistemler kullanılır.[12]
Çeşitleri
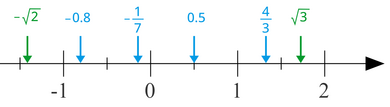
Aritmetikte kullanılan temel sayı türleri doğal sayılar, tam sayılar, tamsayılar, rasyonel sayılar ve reel sayılardır.[13] Doğal sayılar, 1'den başlayıp sonsuza kadar giden tam sayılardır. 0 ve negatif sayıları içermezler. Ayrıca sayma sayıları olarak da bilinir ve şeklinde ifade edilebilir. Doğal sayıların sembolü 'dir.[a]
Tam sayılar, doğal sayılarla aynıdır, tek farkı 0'ı da içermeleridir. şeklinde temsil edilebilir ve sembolü dir.[15][b] Bazı matematikçiler, doğal sayılar kümesine 0'ı dahil ederek doğal sayılar ve tam sayılar arasında bir ayrım yapmazlar.[17] Tam sayılar kümesi, hem pozitif hem de negatif tam sayıları kapsar. Sembolü 'dir ve şeklinde ifade edilebilir.[18]
Doğal ve tam sayıların kullanım biçimlerine göre, bu sayılar kardinal ve ordinal sayıları olarak iki farklı kategoriye ayrılabilir. Kardinal sayılar, bir, iki, üç gibi sayılar, nesnelerin sayısını ifade eder ve "Kaç tane?" sorusuna yanıt verirler. Öte yandan, ordinal sayıları, birinci, ikinci, üçüncü gibi ifadeler, bir dizideki konum veya sıralamayı gösterir ve "Hangi pozisyon?" sorusunu yanıtlarlar. Bu iki sayı türü, matematikte farklı amaçlar için kullanılır ve her biri, belirli bir sorunun cevabını sağlama kapasitesine sahiptir. Kardinal sayılar genellikle nicelikleri, ordinal sayıları ise nesnelerin veya olayların göreceli konumlarını belirtmek için tercih edilir.[19]
Bir sayı, iki tam sayının oranı olarak ifade edilebiliyorsa, bu sayı rasyoneldir. Örneğin, rasyonel sayısı, pay olarak adlandırılan 1 tam sayısının, payda olarak adlandırılan 2 tam sayısına bölünmesiyle elde edilir. Diğer örnekler arasında ve yer almaktadır. Rasyonel sayılar kümesi, paydası 1 olan tüm kesirler olan tam sayıları da kapsamaktadır. Rasyonel sayıların sembolü 'dur.[20] 0.3 ve 25.12 gibi ondalık kesirler, paydaları 10'un bir kuvveti olduğu için, özel bir rasyonel sayı türüdür. Örneğin, 0.3, 'a, 25.12 ise 'e eşittir.[21] Her rasyonel sayı, sonlu veya devirli ondalık bir kesirle ifade edilebilir.[22][c]

İrrasyonel sayılar, iki tam sayının oranı ile ifade edilemeyen sayılardır. Genellikle geometrik büyüklükleri tanımlamak için kullanılırlar. Örneğin, kenarlarının uzunluğu 1 olan bir dik üçgenin hipotenüs uzunluğu irrasyonel bir sayı olan ile ifade edilir. π, başka bir irrasyonel sayı olup bir çemberin çevresi ile çapı arasındaki oranı tanımlar.[23] İrrasyonel sayıların ondalık gösterimi, tekrarlayan basamaklar olmaksızın sonsuzdur.[24] Rasyonel ve irrasyonel sayılar kümeleri birlikte, reel sayılar kümesini oluşturur. Reel sayıların sembolü 'dir.[25] Daha geniş sayı kümeleri arasında karmaşık sayılar ve kuaterniyonlar bulunur.[26]
Sayısal sistemler
Bir rakam, bir sayıyı temsil eden bir semboldür ve sayı sistemleri, sayısal temsillerin oluşturulmasını sağlayan çerçevelerdir.[27] Bu sistemler genellikle, belirli sayılara doğrudan atıfta bulunan sınırlı sayıda temel rakam içerir. Sayı sistemi, bu temel rakamların herhangi bir sayıyı ifade etmek için nasıl birleştirilebileceğini belirler.[28] Sayı sistemleri, basamak değeri esaslı veya basamak değeri esaslı olmayan olarak sınıflandırılır. İlk sayı sistemlerinin tamamı basamak değeri esaslı değildi.[29] Basamak değeri esaslı olmayan sayı sistemlerinde, bir rakamın değeri, sistemdeki konumuna bağlı değildir.[30]
En basit basamak değeri esaslı olmayan sistem, tekli sayı sistemidir. Bu sistem, 1 sayısı için tek bir sembol kullanır. Daha büyük sayılar, bu sembolün tekrarıyla yazılır. Örneğin, 7 sayısı, 1 sembolünün yedi kez tekrarlanmasıyla ifade edilir. Bu sistem, büyük sayıları yazmayı zorlaştırır; bu nedenle, birçok basamak değeri esaslı olmayan sistem, büyük sayıları doğrudan temsil etmek için ek semboller içerir.[31] Birlikte sayma sisteminin varyasyonları, çetele çubukları ve çetele çizgilerinde kullanılır.[32]
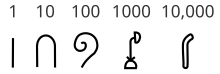
Not listesi
Kaynakça
- ^ a b c "arithmetic." Encyclopædia Britannica Ultimate Reference Suite. Chicago: Encyclopædia Britannica, 2012.
- ^ a b Şablon:Multiref
- ^ Şablon:Multiref
- ^ "aritmetik." Güncel Türkçe Sözlük. Türk Dil Kurumu. Erişim: 21 Mayıs 2013
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Sophian 2017, s. 84
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Musser, Peterson & Burger 2013, s. 358
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Şablon:Multiref
- ^ Ore 1948, s. 10

















































