Matematik ; sayılar, felsefe, uzay ve fizik gibi konularla ilgilenir. Matematikçiler ve filozoflar arasında matematiğin kesin kapsamı ve tanımı konusunda görüş ayrılığı vardır.
Sayı, sayma, ölçme ve etiketleme için kullanılan bir matematiksel nesnedir. En temel örnek, doğal sayılardır. Sayılar, sayı adı (numeral) ile dilde temsil edilebilir. Daha evrensel olarak, tekil sayılar rakam adı verilen sembollerle temsil edilebilir; örneğin, "5" beş sayısını temsil eden bir rakamdır. Yalnızca nispeten az sayıda sembolün ezberlenebilmesi nedeniyle, temel rakamlar genellikle bir rakam sisteminde organize edilir, bu da herhangi bir sayıyı temsil etmenin organize bir yoludur. En yaygın rakam sistemi Hint-Arap rakam sistemidir, bu sistem on temel sayısal sembol, yani rakam kullanılarak herhangi bir negatif olmayan tam sayının temsil edilmesine olanak tanır. Sayılar sayma ve ölçme dışında, etiketlerde, sıralamada ve kodlarda kullanılmak için de sıklıkla kullanılır. Yaygın kullanımda, bir rakam ile temsil ettiği sayı net bir şekilde ayrılmaz.
Matematikte reel sayılar kümesi, Fransızca réel “gerçek” den gelmektedir. Oranlı sayılar kümesinin evrim sürecinden elde edilen bir varsayım kombinasyonudur. Reel sayılar kümesi 
sembolüyle gösterilir.
Bir asal sayı, yalnızca 1'den büyük olup kendisinden küçük iki doğal sayının çarpımı olarak ifade edilemeyen bir doğal sayıdır. 1'den büyük ve asal olmayan doğal sayılara bileşik sayı adı verilir. Örneğin, 5 bir asal sayıdır çünkü onu bir çarpım olarak ifade etmenin mümkün olan yolları, 1 × 5 veya 5 × 1, yalnızca 5 sayısını içermektedir. Ancak, 4 bir bileşik sayıdır çünkü bu, her iki sayının da 4'ten küçük olduğu bir çarpım şeklindedir. Asal sayılar, aritmetiğin temel teoreminden ötürü sayı teorisi alanında merkezi öneme sahiptir: 1'den büyük her doğal sayı, ya bir asal sayıdır ya da asal sayıların çarpımı olarak, sıralamalarından bağımsız bir şekilde, benzersiz olarak çarpanlarına ayrılabilir.
İkiz asallar, aralarındaki fark 2 olan asal sayılar. Örneğin 3-5, 5-7, 11-13 ikiz asallardır. 2-3 çifti hariç iki asal sayı arasındaki fark da zaten en az 2 olabilir.
Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.
Aritmetik; matematiğin sayılar arasındaki ilişkiler ile sayıların problem çözmede kullanımı ile ilgilenen dalı. Aritmetik kavramı ile genellikle sayılar teorisi, ölçme ve hesaplama kastedilir. Bununla birlikte bazı matematikçiler daha karmaşık çeşitli işlemleri de aritmetik başlığı altında değerlendirirler.
Aritmetik ortalama, bir sayı dizisindeki elemanların toplamının eleman sayısına bölünmesi ile elde edilir. İstatistik bilim dalında hem betimsel istatistik alanında hem de çıkarımsal istatistik alanında en çok kullanan merkezi eğilim ölçüsü' dür.
Çokgen, düzlemde herhangi ardışık üçü doğrusal olmayan n tane noktayı ikişer ikişer birleştiren doğru parçalarının oluşturduğu kapalı şekillerdir.
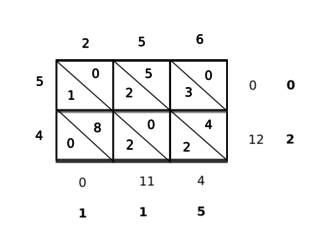
Çarpma, temel aritmetik işlemlerden biridir. Sayılarda çarpma, çarpılan sayının çarpan sayı kadar adedinin toplamının alınması işlemidir.
Johann Carl Friedrich Gauss ya da Gauß, Alman matematikçi, astronom, istatistikçi, olağanüstü katkılardan dolayı "Matematikçilerin prensi" ve "antik çağlardan beri yaşamış en büyük matematikçi" olarak anılır.
Sigma Yunan alfabesinin on sekizinci harfidir. Fenike alfabesinin shin 
harfinden gelmektedir. Diğer harflerden farklı olarak kelimenin sonunda, başındaki ve ortasındaki hâlinden daha farklı yazılır. Kelime ortasında ve başında σ, sonunda ise ς olarak yazılır; büyük harf düzeninde her ikisi de Σ olarak yazılır. Türkçedeki S sesi gibidir. Fakat kendinden sonra Ββ, Υυ, Δδ, Λλ, Μμ, Νν, Ρρ harflerinden biri gelirse, ses Z'ye dönüşür, yani yazılışta s, okunuşta z olur.
Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir nesnedir. a ve b sayıları gerçek olursa karmaşık sayılar şu biçimde gösterilirler:
Dizi, bir sıralı listedir. Bir küme gibi, ögelerden oluşur. Sıralı ögelerin sayısına dizinin uzunluğu denir. Kümenin aksine sıralı ve aynı ögeler dizide farklı konumlarda birkaç kez bulunabilir. Tam olarak bir dizi, tanım kümesi sayılabilen toplam sıralı kümelerden oluşan bir fonksiyon olarak tanımlanabilir. Örneğin doğal sayılar gibi. Diziler bu örnekte olduğu gibi sonlu olabilir. Ya da tüm çift pozitif tam sayılar gibi sonsuz olabilir.
Bir üçgensel sayı, 1'den n'e kadar olan n doğal sayının toplamıdır. Bu sayılara üçgensel denmesinin sebebi, bir üçgen şeklinde dizilebilecek eşit çaplı topların sayılarına karşılık gelmeleridir. n'inci üçgensel sayının formülü şöyledir:
Matematikte 1 - 2 + 3 - 4 + ..., terimlerinin işaretleri sırasıyla değişen ardışık pozitif tam sayıların oluşturduğu sonsuz bir seridir. Serinin ilk m teriminin toplamı, Sigma toplama gösterimi kullanılarak şöyle ifade edilebilir:
Matematiksel çözümlemede Euler özdeşliği olarak adlandırılan ve Leonhard Euler tarafından bulunan eşitlik
Dörtyüzlüsel sayı, üçgen tabanlı ve bir piramidi temsil eden biçimli sayıdır. n. dörtyüzlüsel sayı ilk n üçgensel sayının toplamına eşittir.
Eğlence matematiğinde Harshad sayı rakamları toplamına tam bölünebilen tam sayılara denir. Harshad özelliğini sağlayan sayma tabanına n dersek sayılar n-Harshad veya n-Niven olarak da söylenirler. Hindistanlı matematikçi D. R. Kaprekar tarafından tanımlanmışlardır. "Harshad" kelimesi Sanskritçe harṣa (eğlence) + + da (vermek), kelimelerinin bileşiminden "eğlenceli" anlamındadır. Niven sayı tabiri ise Ivan M. Niven tarafından 1977'de sayma teorisi ile ilgili yayınlanmış olan makaleye dayandırılmıştır.
Eski Mısır matematiği, Eski Mısır'da yaklaşık MÖ 3000 ila 300 yılları arasında, Eski Mısır Krallığı'ndan kabaca Helenistik Mısır'ın başlangıcına kadar geliştirilen ve kullanılan matematiktir. Eski Mısırlılar, saymak ve genellikle çarpma ve kesirleri içeren yazılı matematik problemlerini çözmek için bir sayı sistemi kullandılar. Mısır matematiğinin kanıtı, papirüs üzerine yazılmış, hayatta kalan az sayıda kaynakla sınırlıdır. Bu metinlerden, eski Mısırlıların, mimari mühendislik için yararlı olan üç boyutlu şekillerin yüzey alanını ve hacmini belirlemek gibi geometri kavramlarını ve sabit kesen yöntemi ve ikinci dereceden denklemler gibi cebir kavramlarını anladıkları bilinmektedir.
![{\displaystyle [(nx(n+1))/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec082e602908f35c97d150eff3bd285fc4a15244)
