İçeriğe atla

Anormal manyetik dipol moment

Kuantum elektrodinamiğinde bir parçacığın anormal manyetik momenti, döngülerle beraber Feynman diyagramları ile ifade edilen kuantum mekaniğinin, o parçanın manyetik momentine etkilerinin bir katkısıdır (manyetik dipol momenti olarak da adlandırılan manyetik moment, manyetik kaynağın gücünün bir ölçüsüdür).

Ağaç düzeyinde Feynman diyagramlarına (klasik sonuç olarak düşünülebilecek) karşılık gelen "Dirac" manyetik momenti Dirac denkleminden hesaplanabilir. Genellikle f faktörü ile ifade edilir. Dirac denklemi, g = 2'yi tahmin eder. Elektron gibi parçacıklar için bu klasik sonuç, gözlenen değerden yüzde küçük bir payla ayrılır. Fark, a olarak adlandırılan ve

olarak tanımlanan anormal manyetik momenttir.

Elektron

Fermiyonun manyetik dipol momentine bir döngü düzeltmesi.

Elektronun ilk ve en büyük kuantum mekanik düzeltmesine tekabül eden anormal manyetik momentin bir döngülü katkısı, bitişik diyagramda gösterilen tepe fonksiyonunu hesaplayarak bulunur. Hesaplama nispeten basittir [1] ve aşağıdaki döngü sonucundaki α, ince yapı sabitidir.

Bu sonuç, ilk olarak 1948 yılında Julian Schwinger tarafından bulunmuştur.[2] Bu sonuç, onun mezar taşına oyulmuştur. 2016 yılı itibarıyla, QED formülünün, elektronun anormal manyetik momenti için katsayıları, analitik olarak a3 e kadar bilinir[3] ve α5e kadar hesaplanır:[4][5][6]

QED tahmini, deneysel olarak ölçülen değeri 10'dan fazla anlamlı rakamla kabul eder ve elektronun manyetik momentini fizik tarihindeki en doğru şekilde doğrulanmış tahmin hâline getirir.

Mevcut deneysel değer ve belirsizlik aşağıdaki gibidir:[7]

Bu değere göre, aenin 1 milyar (109) civarında 1 parçanın doğruluğu olduğu bilinmektedir. 1 trilyon (1012) civarında 1 parçanın doğruluğu için g ölçümü gereklidir.

Müon

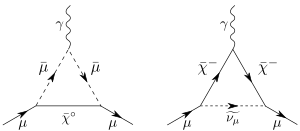
Tek döngülü MSSM, sırasıyla bir nötralino, bir smuon, bir chargino ve bir müon snötrino içeren müon g-2 düzeltmeleridir.

Müonun anormal manyetik momenti, elektrona benzer bir şekilde hesaplanır. Müon anormal manyetik momentin değerinin tahmini üç bölümden oluşur:[8]

İlk iki bileşen, foton ve lepton halkalarını ve sırasıyla W boson, Higgs boson ve Z boson halkalarını temsil eder ve tam olarak ilk prensiplerden hesaplanabilir. Üçüncü terim hadron döngülerini temsil eder ve tek başına teoride doğru olarak hesaplanamaz. Elektron-pozitron (e−e+) çarpışmalarında hadron oranının müon kesitlerine oranının (R) deneysel ölçümlerinden tahmin edilmektedir. Temmuz 2017 itibarıyla, 3,5 standart sapmalarla Standart Model ölçümü uyuşmamaktadır.[9] Standart modelin ötesindeki fiziği önermek bir etki oluşturabilir. Bu, Standart Model ile deney arasındaki uzun süren tutarsızlıklardan biridir.

Brookhaven Ulusal Laboratuvarındaki (BNL) E821 deneyinde sınırlandırıcı bir depolama halkasında dolaştırıldıkları hâlde, sabit bir dış manyetik alanda müon ve antimüonun çalışması incelenmiştir.[10] E821 deneyinde aşağıdaki değer bildirilmiştir:[8]

Fermilab'da "Müon g-2" adlı E821 mıknatısını kullanan yeni bir deney, bu değerin doğruluğunu artıracaktır.[11] 2017 yılında başlayan veri alımı üç yıl boyunca devam edecektir.[12]

Tau

Tau'nun anormal manyetik dipol momenti için Standart Model tahmini aşağıdaki gibidir:

aτ için ölçülen en iyi sınır ise aşağıdaki gibidir:

[13]

Bileşik parçacıklar

Bileşik parçacıklar genellikle çok büyük bir anormal manyetik momente sahiptir. Bu, yüklü kuarklardan oluşan proton ve elektriksel olarak nötr olmasına rağmen manyetik bir momenti olan nötron için geçerlidir.

Kaynakça

  1. ^ Peskin, M. E.; Schroeder, D. V. (1995). "Section 6.3". An Introduction to Quantum Field Theory. Addison-Wesley. ISBN 978-0-201-50397-5. 
  2. ^ Schwinger, J. (1948). "On Quantum-Electrodynamics and the Magnetic Moment of the Electron" (PDF). Physical Review. 73 (4). s. 416. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416. 12 Temmuz 2019 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 17 Mart 2019. 
  3. ^ Laporta, S.; Remiddi, E. (1996). "The analytical value of the electron (g − 2) at order α3 in QED". Physics Letters B. Cilt 379. ss. 283-291. arXiv:hep-ph/9602417 $2. Bibcode:1996PhLB..379..283L. doi:10.1016/0370-2693(96)00439-X. 
  4. ^ Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. (2012). "Tenth-Order QED Contribution to the Electron g−2 and an Improved Value of the Fine Structure Constant". Physical Review Letters. 109 (11). s. 111807. arXiv:1205.5368 $2. Bibcode:2012PhRvL.109k1807A. doi:10.1103/PhysRevLett.109.111807. PMID 23005618. 
  5. ^ Aoyama, Tatsumi; Hayakawa, Masashi; Kinoshita, Toichiro; Nio, Makiko (1 Şubat 2015). "Tenth-Order Electron Anomalous Magnetic Moment — Contribution of Diagrams without Closed Lepton Loops". Physical Review D. 91 (3). s. 033006. arXiv:1412.8284 $2. Bibcode:2015PhRvD..91c3006A. doi:10.1103/PhysRevD.91.033006. 
  6. ^ Nio, Makiko (3 Şubat 2015). QED tenth-order contribution to the electron anomalous magnetic moment and a new value of the fine-structure constant (PDF). Fundamental Constants Meeting 2015. Eltville, Germany. 28 Kasım 2020 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 17 Mart 2019. 
  7. ^ Hanneke, D.; Fogwell Hoogerheide, S.; Gabrielse, G. (2011). "Cavity Control of a Single-Electron Quantum Cyclotron: Measuring the Electron Magnetic Moment" (PDF). Physical Review A. 83 (5). s. 052122. arXiv:1009.4831 $2. Bibcode:2011PhRvA..83e2122H. doi:10.1103/PhysRevA.83.052122. 10 Ağustos 2017 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 17 Mart 2019. 
  8. ^ a b Particle Data Group, and C. Collaboration. "Patrignani et al.,“Review of Particle Physics,”." Chin. Phys. C 40 (2016)., page 32
  9. ^ Giusti, D., et al. "Strange and charm HVP contributions to the muon ($g-2)$ including QED corrections with twisted-mass fermions." arXiv:1707.03019 (2017).
  10. ^ "The E821 Muon (g−2) Home Page". Brookhaven National Laboratory. 19 Mayıs 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 1 Temmuz 2014. 
  11. ^ "Revolutionary muon experiment to begin with 3,200-mile move of 50-foot-wide particle storage ring" (Basın açıklaması). Fermilab. 8 Mayıs 2013. 16 Mart 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Mart 2015. 
  12. ^ Muon Magnet's Moment Has arrived 31 Mayıs 2019 tarihinde Wayback Machine sitesinde arşivlendi., Fermilab press release
  13. ^ Eidelman, S.; Passera, M. (Kasım 2011). "Theory of the tau lepton anomalous magnetic moment". Modern Physics Letters A. 22 (03). ss. 159-179. arXiv:hep-ph/0701260 $2. Bibcode:2007MPLA...22..159E. doi:10.1142/S0217732307022694. 

Konuyla ilgili yayınlar

  • Vonsovskiy, Sergey (1975). Magnetism of Elementary Particles (İngilizce). Mir Publishers. 

Dış bağlantılar

İlgili Araştırma Makaleleri

<span class="mw-page-title-main">Elektron</span> Temel elektrik yüküne sahip atomaltı parçacık

Elektron, eksi bir temel elektrik yüküne sahip bir atomaltı parçacıktır. Lepton parçacık ailesinin ilk nesline aittir ve bileşenleri ya da bilinen bir alt yapıları olmadığından genellikle temel parçacıklar olarak düşünülürler. Kütleleri, protonların yaklaşık olarak 1/1836'sı kadardır. Kuantum mekaniği özellikleri arasında, indirgenmiş Planck sabiti (ħ) biriminde ifade edilen, yarım tam sayı değerinde içsel bir açısal momentum (spin) vardır. Fermiyon olmasından ötürü, Pauli dışarlama ilkesi gereğince iki elektron aynı kuantum durumunda bulunamaz. Temel parçacıkların tamamı gibi hem parçacık hem dalga özelliklerini gösterir ve bu sayede diğer parçacıklarla çarpışabilir ya da kırınabilirler.

Lepton, temel parçacıklardan birisidir ve maddenin yapı taşıdır. En çok bilinen lepton, atomda bulunarak atomun kimyasal özelliklerini belirleyerek neredeyse tüm kimyayı oluşturan elektrondur. İki temel lepton sınıfı vardır: yüklü leptonlar ve nötr leptonlar. Yüklü leptonlar diğer parçacıklarla birleşerek atom ya da pozitronyum gibi bileşik parçacıklar meydana getirirken nötrinolar diğer parçacıklarla etkileşime girmezler ve bu sebepten algılanmaları çok zordur.

<span class="mw-page-title-main">Manyeto optik tuzak</span>

Manyeto optik tuzak, soğuk, kapana kısılmış nötr örnekleri üretebilmek için lazer soğutma ve uzamsal olarak değişen bir manyetik alan kullanan bir cihazdır. Bir MOT'tan elde edilen sıcaklıklar, foton geri tepme sınırının iki veya üç katı olan atomik türe bağlı olarak birkaç mikrokelvin kadar düşük olabilir. Bununla birlikte, çözülmemiş aşırı ince yapıya sahip atomlar için, örneğin;bir MOT'nta elde edilen sıcaklık Doppler soğutimitinden den daha yüksek olacaktır.

Zeeman efekti, ismini Hollandalı fizikçi Pieter Zeeman'dan alan; tayf çizgilerinin, bir manyetik alan olması durumunda birden fazla bileşene ayrılması efektidir. Zeeman alt katmanlarının arasındaki mesafe bir manyetik alan fonksiyonu olduğundan, bu efekt manyetik alanı ölçmek için kullanılabilir.

Stern-Gerlach deneyi Alman fizikçi Otto Stern ve Walther Gerlach tarafından isimlendirilen taneciklerin sapmasının kuantum mekaniği alanında önemli bir deneydir. 1922 yılında Otto Stern ve Walther Gerlach tarafından gerçekleştirilen bu deney, genellikle parçacıkların saçınımını kullanarak kuantum mekaniğinin temel noktalarını açığa çıkarması açısından önemlidir. Bu deney elektronların ve atomların özünde kuantum özelliklerine sahip olduğunu ve ölçülürken kuantum mekaniğinin sistemi nasıl etkilediğini ispat etmek için yapılmaktadır.

Dolanıklık, kuantum mekaniğine özgü bir olgudur. Kuantum fiziğine göre iki benzer parçacık birbiriyle eşzamanlılığa sahiptir. Bu parçacıklar ayrı yerlerde birbirinden eşzamanlı olarak etkilenirler. İki elektron parçası ışık yılına yakın uzaklıkta olsa dahi birbirlerini etkileyebilirler. Bu sayede birbirinden ışık yılına yakın bir uzaklıkta olan bir elektron kendi çevresi etrafında sağa dönerken diğer bir elektron parçası sola dönecektir.

Ferromanyetik rezonans veya FMR, ferromıknatıs malzemeleri incelemek için kullanılan bir spektroskopi yöntemidir. Spin dalgaları ve spin dinamikleri inceleyen için standart bir araçtır. FMR, elektron paramanyetik rezonansa (EPR) çok benzediği gibi, ayrıca nükleer manyetik rezonansa (NMR) da biraz benzer. Tek farkı FMR, dipolar bağlı fakat eşsiz olan elektronların manyetik momentteki mıknatıslanma sonucunu incelerken; NMR ise, atomik veya moleküler orbitallerin etrafında, sıfır olmayan nükleer spin çekirdeği gibi dolaşan atomik çekirdeğin manyetik momentini inceler.

Landau Kutbu veya diğer adıyla Moskova Sıfırı olarak bilinen, kuantum (nicem) alan kuramının sonsuz olduğu bağlaşım sabitindeki momentum (devinim) ölçeğidir. Bu olasılık Lev Landau ve meslektaşları tarafından belirtilmiştir. Bu bağlaşım sabiti, yeniden boylandırım grubun arkasında yatan temel fikirlerden olan momentum (devinim) ölçeğine dayanmaktadır.

<span class="mw-page-title-main">Rydberg atomu</span>

Rydberg atomu çok yüksek temel nicem sayılı bir veya iki elektrona sahip bir uyarılmış atomdur Bu atomlar elektrik ve manyetik alana abartılı tepkiler vermeyi de içinde barındıran, uzun bozunma devri ve yaklaşık elektron dalgafonksiyonları, bazı şartlar altında çekirdekler etrafındaki elektronların klasik yörüngeleri gibi kendilerine has birçok özelliğe sahiptir. Çekirdek elektronları dış elektronları çekirdeğin elektrik alanından kalkanlar, öyle ki belirli bir mesafeden hidrojen atomundaki bir elektronun tecrübe ettiği gibi elektrik potansiyeli belirleyicidir.

Kuantum mekaniğinde, spin-yörünge etkileşimi(spin-yörünge etkisi, spin-yörünge bağlaşımı) parçacığın dönüşünün hareketiyle etkileşimidir. En çok bilinen örnek ise, elektronların dönüşü ile elektronların çekirdek etrafındaki dönüşünden dolayı oluşan manyetik alandan dolayı oluşan elektromanyetik etkileşim ve buna bağlı olan elektronların atomik enerji seviyesindeki değişim. Bu tayf çizgilerinden saptanabilir. Buna benzer bir diğer etki proton ve nötronların çekirdekte dönmesinden dolayı oluşan olan Açısal momentum ve güçlü nükleer kuvvet, nükleer kabuk modelindeki değişime neden olur. Spintronik alanında, yarı iletkenlerde ve diğer materyallerde spin yörünge etkileşimi yeni teknolojik gelişimler için araştırılmaktadır.

Kerr–Newman metriği genel relativitide yüklü, dönen kütlelerin çevresindeki uzay zaman geometrisini tarif eden Einstein–Maxwell denklemlerinin çözümüdür. Bu çözüm astrofizik alanındaki fenomenler için pek faydalı sayılmaz çünkü gözlemlenebilen astronomik objeler kayda değer net yük taşımazlar. Bu çözüm uygulama alanı yerine daha çok teorik fizik ve matematiksel ilginin bir sonucudur..

Breit denklemi, Gregory Breit tarafından 1929'da Dirac denklemine dayalı olarak türetilmiş kökler kuralının ilk kuralına göre iki ya da daha fazla kütleli spini -1/2 olan parçacıkların elektromanyetizma açısından etkileşimini tanımlayan rölativistik dalga denklemidir. Manyetik etkileşimlerin ve  kuralına göre gecikme etkisinin nedeni açıklar. Diğer kuantum elektrodinamik etkileri ihmal edildiğinde, bu denklemin deney ile iyi bir uyum içinde olduğu görülmüştür. Bu denklem başlangıçta Darwin Lagrangian tarafından türetildi ancak daha sonra Wheeler-Feynman emme teorisi ve en sonunda kuantum elektrodinamiği tarafından doğrulandı.

Nötrino salınımları, üretilen ve belirli bir lepton türü olan bir nötrinonun daha sonradan farklı bir tür olarak ölçülebilmesine denen bir kuantum mekaniği fenomenidir. Uzaya yayılan nötrinoların türleri periyodik olarak değişir.

<span class="mw-page-title-main">Manyetik tek kutup</span>

Manyetik monopol, parçacık fiziğinde yalıtılmış tek bir manyetik kutbu olan kuramsal bir temel parçacıktır. Daha teknik terimlerle açıklanacak olursa, bir manyetik monopol net manyetik yükü olan bir parçacıktır. Bu teori köklerini manyetik monopollerin varlığını öngören parçacık teorileri, özellikle büyük birleşim ve süper sicim teorilerinden alır. Çubuk şeklindeki mıknatısların manyetik alanı ve elektromanyetikler manyetik monopollerden kaynaklanmazlar. Manyetik monopollerin varlığını kanıtlayan herhangi bir deneysel veri yoktur. Bazı yoğun madde sistemleri efektif manyetik monopol, quasi parçacığını veya matematiksel olarak manyetik monopollerle benzeşen bazı fenomenleri barındırır.

Parton, Richard Feynman tarafından ortaya atılan bir hadron modelidir. Stanford Doğrusal Hızlandırıcı Merkezi'nde (SLAC) 1968 yılında yapılan derin inelastik saçılma deneyleri, protonun daha küçük, nokta benzeri parçacıklardan oluştuğunu ve böylece bir temel parçacık olmadığını gösterdi. O dönemde fizikçiler bu nesneleri kuarklar ile ilişkilendirmek konusunda tereddütlü olduklarından parçacıklar, Feynman tarafından türetilen "parton" olarak adlandırdı. Bu deneyler sırasında gözlemlenen cisimler, diğer çeşnilerin de keşfedilmesiyle daha sonra yukarı ve aşağı kuark olarak tanımlanacaktı. Buna rağmen parton, hadronların bileşenlerini tanımlayan ortak bir terim olarak kullanımda kaldı.

Ksi baryonları, birinci çeşni nesillerinden bir kuarka, daha yüksek çeşnili nesillerinden ise iki kuarka sahip, Ξ sembolüyle gösterilen hadron parçacığı ailesidir. Bu nedenlerden ötürü bu tip parçacıklar birer baryondur, toplam izospinleri 1/2'dir ve nötr olabildikleri gibi +2, +1 ya da -1 temel yüke sahip olabilirler. Yüklü Ksi baryonları ilk kez 1952'de, Manchester grubu tarafından gerçekleştirilen kozmik ışın deneyleri sırasında gözlemlenmiştir. Nötr Ksi baryonlarının ilk kez gözlemlenmesi ise 1959'da, Lawrence Berkeley Ulusal Laboratuvarı'nda gerçekleştirildi. Kararsız durumları, bozunma zinciri sonucunda daha hafif parçacıklara bozunmaları sebebiyle geçmişte çağlayan parçacıklar olarak da anılmaktaydılar.

Henry Michael Foley, Amerikalı deneysel fizikçi.

Orbiton, holonlar ve spinonlar ile birlikte, katıların içindeki elektronların spin-yük ayrımı sırasında bölünerek oluşturduğu ve mutlak sıfıra yakın sıcaklıklarda hapsedilen sanki parçacıktır. Elektron, teorik olarak her zaman bu üç sanki parçacığın bir bağlı durumu olarak kabul edilmektedir. Bunlardan orbitron, elektronun yörüngesel konumunu taşımaktadır. Belli şartlar altında ise hapis durumlarından kurtularak bağımsız parçacıklar olarak davranabilmektedirler.

Vakum kutuplaşması ya da vakum polarizasyonu, arka plandaki bir elektromanyetik alanın, özgün elektromanyetik alanı oluşturan yük ve akımların dağılımlarını değiştiren sanal elektron-pozitron çiftleri üretmesidir. Zaman zaman ayar bozonunun öz enerjisi olarak da tanımlanmaktadır.

Manyetik hidrodinamikte, manyetik Reynolds sayısı (Rm) bir boyutsuz nicelik olup, bir iletken ortamın hareketiyle bir manyetik alanın adveksiyon veya indüksiyonunun, manyetik difüzyona göreceli etkilerini tahmin eder. Bu sayı, akışkanlar mekaniğindeki Reynolds sayısının manyetik bir benzeridir ve genellikle şu şekilde tanımlanır:


Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.